2005年上海市高考数学最新测试卷
(七校联考:华师大一附中、曹杨二中、市西中学、市三女子、控江、格致、市北)
一、填空题(4′×12)
1.函数![]() 图象恒过定点
图象恒过定点![]() ,若
,若![]() 存在反函数
存在反函数![]() ,则
,则![]() 的图象必过定点
的图象必过定点 ![]() 。
。
2.已知集合![]() ,集合
,集合![]() ,则集合
,则集合![]()
![]()
![]() 。
。
3.若角![]() 终边落在射线
终边落在射线![]() 上,则
上,则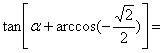
![]() 。
。
4.关于![]() 的方程
的方程![]() 有一实根为
有一实根为![]() ,则
,则![]()
![]() 。
。
5.数列![]() 的首项为
的首项为![]() ,且
,且![]() ,记
,记![]() 为数列
为数列![]() 前
前![]() 项和,则
项和,则![]()
![]()
![]() 。
。
6.新教材同学做:
若![]() 满足
满足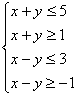 ,则目标函数
,则目标函数![]() 取最大值时
取最大值时![]()
![]() 。
。
老教材同学做:
若![]() 的展开式中第3项为常数项,则展开式中二项式系数最大的是第
的展开式中第3项为常数项,则展开式中二项式系数最大的是第 ![]() 项。
项。
7.已知函数![]() ,若对任意
,若对任意![]() 有
有![]() 成立,则方程
成立,则方程![]() 在
在![]() 上的解为
上的解为 ![]() 。
。
8.新教材同学做:
某校高二(8)班四位同学的数学期中、期末和平时成绩可分别用矩阵
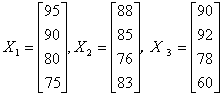 表示,总评成绩分别按期中、期末和平时成绩的30%、40%、30%的总和计算,则四位同学总评成绩的矩阵
表示,总评成绩分别按期中、期末和平时成绩的30%、40%、30%的总和计算,则四位同学总评成绩的矩阵![]() 可用
可用![]() 表示为
表示为 ![]() 。
。
老教材同学做:
某足球队共有11名主力队员和3名替补队员参加一场足球比赛,其中有2名主力和1名替补队员不慎误服违禁药物,依照比赛规定,比赛后必须随机抽取2名队员的尿样化验,则能查到服用违禁药物的主力队员的概率为 ![]() 。(结果用分数表示)
。(结果用分数表示)
9.将最小正周期为![]() 的函数
的函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到偶函数图象,则满足题意的
个单位,得到偶函数图象,则满足题意的![]() 的一个可能值为
的一个可能值为 ![]() 。
。
10.据某报《自然健康状况》的调查报道,所测血压结果与相应年龄的统计数据如下表,观察表中数据规律,并将最适当的数据填入表中括号内。
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | …… |
| 收缩压 (水银柱/毫米) | 110 | 115 | 120 | 125 | 130 | 135 | (140) | 145 | …… |
| 舒张压 (水银柱/毫米) | 70 | 73 | 75 | 78 | 80 | 73 | 85 | (88) | …… |
 11.若函数
11.若函数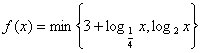 ,其中
,其中![]() 表示
表示![]() 两者中的较小者,
两者中的较小者,
则![]() 的解为
的解为 ![]() 。
。
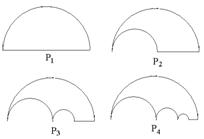
12.如图,![]() 是一块半径为1的半圆形纸板,在
是一块半径为1的半圆形纸板,在![]() 的左下端剪去一个半径
的左下端剪去一个半径
为![]() 的半圆得到图形
的半圆得到图形![]() ,然后依次剪去一个更小的半圆(其直径是前
,然后依次剪去一个更小的半圆(其直径是前
一个被剪掉半圆的半径)可得图形![]() ,记纸板
,记纸板![]() 的面积为
的面积为![]() ,则
,则![]()
![]() 。
。
二、选择题(4′×4)
13.已知![]() 满足
满足![]() ,则下列选项中不一定能成立的是
( C
)
,则下列选项中不一定能成立的是
( C
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
14.下列命题正确的是 ( C )
A、若![]() ,
,![]() ,则
,则![]() 。
。
B、函数![]() 的反函数为
的反函数为![]() 。
。
C、函数![]() 为奇函数。
为奇函数。
D、函数![]() ,当
,当![]() 时,
时,![]() 恒成立。
恒成立。
15.函数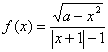 为奇函数的充要条件是
( B
)
为奇函数的充要条件是
( B
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
16.不等式![]() 对任意
对任意![]() 都成立,则
都成立,则![]() 的取值范围为
( B
)
的取值范围为
( B
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、解答题:
17.(本题满分12分)
新教材同学做:在![]() 中,角
中,角![]() 所对边分别为
所对边分别为![]() ,已知
,已知![]()
![]()
![]()
![]()
![]() 0
0
0 ![]()
![]() = 0,求
= 0,求![]() 的面积S。
的面积S。
![]() 0 1
0 1
解:计算行列式的值,得 ![]() ,由正弦定理,得
,由正弦定理,得![]()
即![]() ,∴
,∴![]() ,再由
,再由![]() ,得
,得![]() ,∴
,∴![]()
∴![]() 是直角三角形,∴
是直角三角形,∴![]() 。
。
老教材同学做:在![]() 中,角
中,角![]() 所对边分别为
所对边分别为![]() ,已知
,已知![]()
![]() ,求
,求![]() 的面积S。
的面积S。
解:由![]() 及正弦定理,得
及正弦定理,得 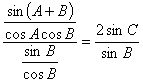 ,即
,即 ![]() ,(其余同上)
,(其余同上)
18.(本题满分12分)
设复数![]() ,复数
,复数![]() ,且
,且![]() 在复平面上所对应点在直线
在复平面上所对应点在直线![]() 上,求
上,求![]() 的取值范围。
的取值范围。
解: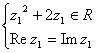
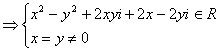
![]()
![]()
![]()
![]()
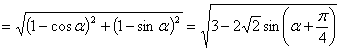 ∴
∴![]()
![]()
19.(本题满分14分)
已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() 。
。
(1)当![]() 时,求集合
时,求集合![]() ;
;
(2)若![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
解:(1)![]() 时,不等式为
时,不等式为![]() ,解之,得
,解之,得 ![]()
(2)![]() 时,
时,![]()
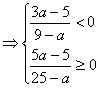
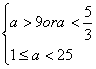
![]()
![]() 时,不等式为
时,不等式为![]() , 解之,得
, 解之,得 ![]() ,
,
则 ![]() , ∴
, ∴![]() 满足条件
满足条件
综上,得 ![]() 。
。
20.(本题满分14分)
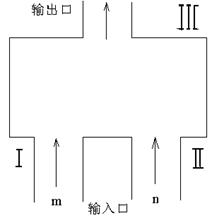 如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数
如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数![]() 时,输出结果记为
时,输出结果记为![]() ,且计算装置运算原理如下:
,且计算装置运算原理如下:
①
若Ⅰ、Ⅱ分别输入1,则![]() ;②若Ⅰ输入固定的正整数,
;②若Ⅰ输入固定的正整数,
Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,
Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:
(1)![]() 的表达式
的表达式![]() ;(2)
;(2)![]() 的表达式
的表达式![]() ;
;
(3)若Ⅰ、Ⅱ都输入正整数![]() ,则输出结果
,则输出结果![]() 能否为2005?
能否为2005?
若能,求出相应的![]() ;若不能,则请说明理由。
;若不能,则请说明理由。
解:(1)![]()
(2)![]()
(3)![]() ,∵
,∵![]() ,
,![]()
∴![]() 输出结果不可能为
输出结果不可能为![]() 。
。
21.(本题满分16分)
对数列![]() ,规定
,规定![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() 。
。
对自然数![]() ,规定
,规定![]() 为
为![]() 的
的![]() 阶差分数列,其中
阶差分数列,其中![]() 。
。
(1)已知数列![]() 的通项公式
的通项公式![]() ,试判断
,试判断![]() ,
,![]() 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列![]() 首项
首项![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式。
的通项公式。
(3)对(2)中数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切自然
对一切自然![]() 都成立?若存在,求数列
都成立?若存在,求数列![]() 的通项公式;若不存在,则请说明理由。
的通项公式;若不存在,则请说明理由。
解:(1)![]() ,∴
,∴![]() 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
![]()
∴![]() 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
(2)![]() ,即
,即![]() ,即
,即![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,猜想:
,猜想:![]()
证明:ⅰ)当![]() 时,
时,![]() ;
;
ⅱ)假设![]() 时,
时,![]()
![]() 时,
时,![]() 结论也成立
结论也成立
∴由ⅰ)、ⅱ)可知,![]()
(3)![]() ,即
,即 ![]()
∵![]()
∴存在等差数列![]() ,
,![]() ,使得
,使得![]() 对一切自然
对一切自然![]() 都成立。
都成立。
22.(本题满分18分)
已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() (
(![]() 为常数)。
为常数)。
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求
时,求![]() 在
在![]() 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的![]() ,并猜想
,并猜想![]() 在
在![]() 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当![]() 时,证明:函数
时,证明:函数![]() 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线![]() 上。
上。
解:(1)![]() 时,
时,![]() , 则
, 则 ![]()
∵函数![]() 是定义在
是定义在![]() 上的奇函数,即
上的奇函数,即![]()
∴![]() ,即
,即 ![]() ,又可知
,又可知 ![]()
∴函数![]() 的解析式为
的解析式为 ![]() ,
,![]()
(2)![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]()
∵ 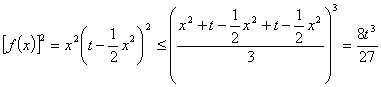
∴![]() ,即
,即 ![]()
![]() 时,
时,![]() 。
。
猜想![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为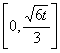 。
。
(3)![]() 时,任取
时,任取![]() ,∵
,∵![]()
∴![]() 在
在![]() 上单调递增,即
上单调递增,即![]() ,即
,即![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴当![]() 时,函数
时,函数![]() 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线![]() 上。
上。