08届高考文科数学第二次调研考试试题
第Ⅰ卷(选择题,共50分)
一.选择题:本大题共l0小题,在每小题给出的四个选项中.只有一项是符合题目要求的.每小题5分,满分50分.
1.命题“![]() ”的否命题是( ).
”的否命题是( ).
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
2.为确保信息安全,信息需加密传输,发送方由明文![]() 密文(加密),接受方由密文
密文(加密),接受方由密文![]() 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文![]() 对应密文
对应密文![]() ,例如,明文
,例如,明文![]() 对应密文
对应密文![]() .当接受方收到密文
.当接受方收到密文![]() 时,则解密得到的明文为( ).
时,则解密得到的明文为( ).
A. 4,6,1,7 B. 7,6,1,4 C. 6,4,1,7 D. 1,6,4,7
3.已知向量![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() 的值等于( ).
的值等于( ).
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
4.已知椭圆的长轴长是短轴长的![]() 倍,则椭圆的离心率等于(
).
倍,则椭圆的离心率等于(
).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在一次射击训练中,一小组的成绩如下表:
| 环数 |
|
|
|
| 人数 |
|
|
已知该小组的平均成绩为![]() 环,那么成绩为
环,那么成绩为![]() 环的人数是(
).
环的人数是(
).
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
6. 下列函数为奇函数的是( ).
![]() .
.
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
7. 下列四个几何体中,每个几何体的三视图有且仅有两个视图相同的是( ).
 |
A.①② B.①③ C.①④ D.②④

8.如果执行下面的程序框图,那么输出的![]() ( ).
( ).
A.2450 B.2500 C.2550 D.2652
9.将函数![]() 的图象先向左平移
的图象先向左平移![]() ,然后将所得
,然后将所得
图象上所有的点的横坐标变为原来的![]() 倍(纵坐标不变),则
倍(纵坐标不变),则
所得到的图象对应的函数解析式为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知全集R,集合![]() ,若
,若![]() ,则有( ).
,则有( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共100分)
二.填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11.化简:![]() .
.
12. 已知![]() 是定义在R上的函数,且对任意
是定义在R上的函数,且对任意![]() ,都有:
,都有:![]() ,又
,又![]() 则
则![]() .
.
13.若实数![]() 满足条件
满足条件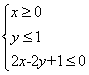 ,则目标函数
,则目标函数![]() 的最大值为
.
的最大值为
.
 14.
(坐标系与参数方程选做题)极坐标系中,圆
14.
(坐标系与参数方程选做题)极坐标系中,圆![]() 上的动点到直线
上的动点到直线![]() 的距离的最大值是
.
的距离的最大值是
.
15.
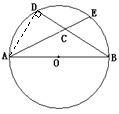
(几何证明选讲选做题)如右图所示,![]() 是圆
是圆![]() 的直径,
的直径,
![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
三.解答题:本大题共6小题,满分80分.解答须写出文字说明.证明过程和演算步骤.
16.(本小题12分)
在△ABC中,![]() 是角
是角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)设![]() ,求
,求![]() 的最小值.
的最小值.
17.(本小题14分)
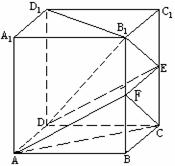
已知:正方体![]() ,
,![]() ,E为棱
,E为棱![]() 的中点.
的中点.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 求证:![]() 平面
平面![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
18.(本小题12分)
有朋自远方来,已知他乘火车、轮船、汽车、飞机来的概率分别是![]() .
.
(Ⅰ)求他乘火车或飞机来的概率;
(Ⅱ)求他不乘轮船来的概率;
(Ⅲ)如果他来的概率为![]() ,请问他有可能是乘何种交通工具来的?
,请问他有可能是乘何种交通工具来的?
19.(本小题14分)
设函数![]() 的图象关于原点对称,
的图象关于原点对称,![]() 的图象在点
的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,且当
,且当![]() 时
时![]() 有极值.
有极值.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的所有极值.
的所有极值.
20. (本小题14分)
已知圆![]() :
:![]() 和圆
和圆![]() ,直线
,直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ;圆
;圆![]() 的圆心在射线
的圆心在射线![]() 上,圆
上,圆![]() 过原点,且被直线
过原点,且被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求直线![]() 的方程;
的方程;
(Ⅱ)求圆![]() 的方程.
的方程.
21.(本小题14分)
已知数列![]() 是等差数列,
是等差数列, ![]() ;数列
;数列![]() 的前n项和是
的前n项和是![]() ,且
,且![]() .
.
(Ⅰ) 求数列![]() 的通项公式;
的通项公式;
(Ⅱ) 求证:数列![]() 是等比数列;
是等比数列;
(Ⅲ) 记![]() ,求
,求![]() 的前n项和
的前n项和![]() .
.
参考答案
| 题号 |
|
|
|
|
|
|
|
|
|
|
| 答案 |
|
|
|
|
|
|
|
|
|
|
1.解析:命题“![]() ”的否命题是:“
”的否命题是:“![]() ”,故选C.
”,故选C.
2.解析:由已知,得: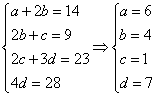 ,故选
,故选![]() .
.
3.解析:若![]() ,则
,则![]() ,解得
,解得![]() .故选
.故选![]() .
.
4.解析:由题意得![]() ,又
,又![]() .
.
故选![]() .
.
5.解析:设成绩为![]() 环的人数是
环的人数是![]() ,由平均数的概念,得:
,由平均数的概念,得:![]() .
.
故选![]() .
.
6.解析:![]() 是偶函数;
是偶函数;![]() 是指数函数;
是指数函数;![]() 是对数函数.故选
是对数函数.故选![]() .
.
7.解析:①的三视图均为正方形;②的三视图中正视图.侧视图为相同的等腰三角形,俯视图为圆;④的三视图中正视图.侧视图为相同的等腰三角形,俯视图为正方形.故选![]() .
.
8.解析:程序的运行结果是![]() ,选
,选![]() .
.
9.解析:![]() 的图象先向左平移
的图象先向左平移![]() ,横坐标变为原来的
,横坐标变为原来的![]() 倍
倍![]() .答案:
.答案:![]() .
.
10.解析:特殊值法:令![]() ,有
,有![]() .故选
.故选![]() .
.
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
|
|
|
|
11.解析:![]() .
.
12.解析:令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
 同理得
同理得![]() 即当
即当![]() 时,
时,![]() 的值以
的值以![]() 为周期,
为周期,
所以![]() .
.
13.解析:由图象知:当函数![]() 的图象过点
的图象过点![]() 时,
时,
![]() 取得最大值为2.
取得最大值为2.
 14. (坐标系与参数方程选做题)解析:将极坐标方程转化成直角坐标方程,圆
14. (坐标系与参数方程选做题)解析:将极坐标方程转化成直角坐标方程,圆![]() 上的动点到直线
上的动点到直线![]() 的距离的最大值就是圆心
的距离的最大值就是圆心![]() 到直线
到直线![]() 的距离
的距离![]() 再加上半径
再加上半径![]() .故填
.故填![]() .
.
15.
(几何证明选讲选做题)解析:连结![]() ,
,
则在![]() 和
和![]() 中:
中:![]() ,
,
且![]() ,所以
,所以![]() ,
,
故![]() .
.
三.解答题:本大题共6小题,满分80分.解答须写出文字说明.证明过程和演算步骤.
16.析:主要考察三角形中的边角关系、向量的坐标运算、二次函数的最值.
解:(Ⅰ)∵![]() ,∴
,∴![]() , ………………3分
, ………………3分
又∵![]() ,∴
,∴![]() . ……………………………………………5分
. ……………………………………………5分
(Ⅱ)![]() ……………………………………………6分
……………………………………………6分
![]() , ………………………8分
, ………………………8分
 ∵
∵![]() ,∴
,∴![]() . ……………10分
. ……………10分
∴当![]() 时,取得最小值为
时,取得最小值为![]() . …………12分
. …………12分
17.析:主要考察立体几何中的位置关系、体积.
解:(Ⅰ)证明:连结![]() ,则
,则![]() //
//![]() , …………1分
, …………1分
∵![]() 是正方形,∴
是正方形,∴![]() .∵
.∵![]() 面
面![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() 面
面![]() . ………………4分
. ………………4分
∵![]() 面
面![]() ,∴
,∴![]() ,
,
 ∴
∴![]() . …………………………………………5分
. …………………………………………5分
(Ⅱ)证明:作![]() 的中点F,连结
的中点F,连结![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]()
![]()
![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴ ![]() . ………7分
. ………7分
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,∴
,∴![]() .
.
 ∴四边形
∴四边形![]() 是平行四边形,
是平行四边形,![]() //
//![]() ,
,
∵![]() ,
,![]() ,
,
∴平面![]() 面
面![]() . …………………………………9分
. …………………………………9分
又![]() 平面
平面![]() ,∴
,∴![]() 面
面![]() . ………………10分
. ………………10分
(3)![]() . ……………………………11分
. ……………………………11分
![]() . ……………………………14分
. ……………………………14分
18.析:主要考察事件的运算、古典概型.
解:设“朋友乘火车、轮船、汽车、飞机来”分别为事件![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,且事件
,且事件![]() 之间是互斥的.
之间是互斥的.
(Ⅰ)他乘火车或飞机来的概率为![]() ………4分
………4分
(Ⅱ)他乘轮船来的概率是![]() ,
,
所以他不乘轮船来的概率为![]() . ………………8分
. ………………8分
(Ⅲ)由于![]()
![]()
![]()
![]()
![]() ,
,
所以他可能是乘飞机来也可能是乘火车或汽车来的. …………………12分
19.析:主要考察函数的图象与性质,导数的应用.
解:(Ⅰ)由函数![]() 的图象关于原点对称,得
的图象关于原点对称,得![]() ,………………1分
,………………1分
∴![]() ,∴
,∴![]() . …………2分
. …………2分
∴![]() ,∴
,∴![]() . ……………………………4分
. ……………………………4分
∴![]() ,即
,即![]() . ……………………6分
. ……………………6分
∴![]() . ……………………………………………………7分
. ……………………………………………………7分
(Ⅱ)由(Ⅰ)知![]() ,∴
,∴![]() .
.
由![]() ,∴
,∴![]() . …………………9分
. …………………9分
|
|
|
|
|
|
|
|
|
| 0 | + | 0 |
|
|
| ↘ | 极小 | ↗ | 极大 | ↘ |
∴![]() . ………………………14分
. ………………………14分
20.析:主要考察直线.圆的方程,直线与圆的位置关系.
解:(Ⅰ)(法一)∵点![]() 在圆
在圆![]() 上, …………………………2分
上, …………………………2分
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() . ……………………………5分
. ……………………………5分
(法二)当直线![]() 垂直
垂直![]() 轴时,不符合题意. ……………………………2分
轴时,不符合题意. ……………………………2分
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
则圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,即:
,即:![]() ,解得
,解得![]() ,……4分
,……4分
∴直线![]() 的方程为
的方程为![]() . ……………………………………………5分
. ……………………………………………5分
(Ⅱ)设圆![]() :
:![]()
![]() ,∵圆
,∵圆![]() 过原点,∴
过原点,∴![]() .
.
∴圆![]() 的方程为
的方程为![]()
![]() .…………………………7分
.…………………………7分
∵圆![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() ,∴圆心
,∴圆心![]() 到直线
到直线![]() :
:![]() 的距离:
的距离:
![]() . …………………………………………9分
. …………………………………………9分
整理得:![]() ,解得
,解得![]() 或
或![]() . ……………………………10分
. ……………………………10分
∵![]() ,∴
,∴![]() . …………………………………………………………13分
. …………………………………………………………13分
∴圆![]() :
:![]() . ……………………………………14分
. ……………………………………14分
21.析:主要考察等差、等比数列的定义、式,求数列的和的方法.
解:(Ⅰ)设![]() 的公差为
的公差为![]() ,则:
,则:![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴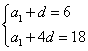 ,∴
,∴![]() . ………………………2分
. ………………………2分
∴![]() . …………………………………………4分
. …………………………………………4分
(Ⅱ)当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() .
…………………5分
.
…………………5分
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() . …………………………7分
. …………………………7分
∴![]() . ……………………………………………………………8分
. ……………………………………………………………8分
∴![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列. …………………………………9分
为公比的等比数列. …………………………………9分
(Ⅲ)由(2)可知:![]() . ……………………………10分
. ……………………………10分
∴![]() . …………………………………11分
. …………………………………11分
∴![]() .
.
∴![]() .
.
∴![]()
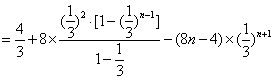
![]() . ………………………………………13分
. ………………………………………13分
∴![]() . …………………………………………………14分
. …………………………………………………14分