高考适应性训练（三）

高考适应性训练（三）

一. 选择题：

1、与曲线关于y轴对称的曲线为（　　）

　　 A. 　　 　　　　B. 　　　　 C. 　　　　　　 D.

2、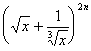展开式的第6项系数最大，则其常数项为（　　）

　 　 A. 120　　　　 　B. 252　　　　　　　C. 210　　 　　　 　D. 45

3、 过原点的直线与圆相切，若切点在第二象限，则该直线的方程是（　　）

　　A. 　　　　B. 　　　　　　　C. 　　　　　 D.

4、长方体一个顶点上三条棱的长分别是6、8、10，且它的八个顶点都在同一个球面上，这个球的表面积是（　　）

　　A. 　　　　　　 B. 　　　　　　　C. 　　　　　　　D.

5、设项数为8的等比数列的中间两项与的两根相等，则数列的各项相乘的积为（　）

　　A. 64　　　　　　 　　B. 8　　　　　　　C. 16　 　　　 　　 D. 32

6、设函数，则的值为（　　）

　　A. a　　　　　　　 B. b　　　　　　　 C. a、b中较小的数　　　　　　 D. a、b中较大的数

7、 已知是R上的偶函数，是R上的奇函数，且，若，则的值为（　　）

A. 2　　　　　　　 B. 0　　　　　　　 C. -2　　　 　　　　　　　D. ±2

8、双曲线的两个焦点为，点P在双曲线上，若，则点P到y轴的距离为_____。

9、 把正n棱柱的顶点相连接的直线（不包括棱柱的边）共有___条。

10、设数列的通项公式为且满足，则实数的取值范围是_______。

11、已知函数f(x)=3^x+k(k为常数)，A（－2k, 2）是函数y=f^－1（x）图象上的点。

（I）求实数k的值及函数y=f^－1(x)的解析式；

（II）将y=f^－1(x)的图象按向量（3，0）平移，得到函数y=g(x)的图象。

若2f^－1(x+)－g(x)≥1恒成立，试求实数m的取值范围。

解：（I）∵A（－2k, 2）是函数y=f^－1(x)图象上的点。

∴B（2，－2K）是函数y=f(x)上的点。　　 ∴2k=3²+k

∴k=－3, ∴y=f(x)=3^x－3　　　　　 ∴y=f^－1(x)=log₃(x+3),(x>－3)

（II）将y=f^－1(x)的图象按向量=（3，0）平移，得函数y=g(x)=log₃x(x>0)

要使2f^－1(x+)－g(x)≥1 恒成立，　 即使2log₃(x+)－log₃­x≥1恒成立。

所以有x+≥3在x>0时恒成立，只须（x+）_min≥3。

又x+(当且仅当x=时取等号)

∴（x+）_min=4　　　　　  只须4≥3，即m≥。

∴实数m的取值范围为

12．设G、M分别为不等边△ABC的重心与外心，A（－1，0）、B（1，0），GM//AB。

（1）求点C的轨迹方程；

（2）设点C的轨迹为曲线E，是否存在直线，使过点（0.1）并与曲线E交于P、Q两点，且满足？若存在，求出直线的方程，若不存在，说明理由。

注：三角形的重心的概念和性质如下：设△ABC的重心，且有。

解：(I)点C的轨迹方程为 x²+

(II)假设存在直线满足条件，设直线方程为y=kx+1,

由消去x，得（3+k²）x²+2kx－2=0

∵直线与曲线E并于P、Q两点，∴△=4k²+8(2+k²)>0

设P(x₁,y₁)，Q（x₂,y₂）,则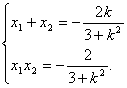　

∵　　　　  ∴x₁x₂+y₁y₂=－2,即x₁x₂+(kx₁+1)(kx₂+1)=－2.

(1+k²)x₁x₂+k(x₁+x₂)+3=0, (1+k²)

解得k²=7, ∴k=±　　 故存在直线：y=±+1,使得