08届高考数学复习每周天天练试题
(推理与证明预测)2008.3
班级 姓名 学号
(一)
1.设![]() ,…,
,…,![]() ,n∈N,则
,n∈N,则![]()
2.已知![]()
![]() ,猜想
,猜想![]() 的表达式为
的表达式为
3.如一个凸多面体是n棱锥,则这个凸多面体的所有顶点所确定的直线共有_____条,这些直线中共有![]() 对异面直线,则
对异面直线,则![]() ;f(n)=
(用数字或n的解析式表示)
;f(n)=
(用数字或n的解析式表示)
 4.在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第
4.在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第![]() 堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第
堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第![]() 堆第
堆第![]() 层就放一个乒乓球,以
层就放一个乒乓球,以![]() 表示第
表示第![]() 堆的乒乓球总数,则
堆的乒乓球总数,则![]() ;
;![]() (答案用
(答案用![]() 表示)
表示)
5.设平面内有![]() 条直线
条直线![]() ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用![]() 表示这
表示这![]() 条直线交点的个数,则
条直线交点的个数,则![]() =____________;当
=____________;当![]() 时,
时,![]() .(用
.(用![]() 表示)
表示)
(二)
1. ![]() ,观察以上两等式,请写出一个与以上两式规律相同的一个正确等式
,观察以上两等式,请写出一个与以上两式规律相同的一个正确等式
2.若![]() 在椭圆
在椭圆![]() 外 ,则过Po作椭圆的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是
外 ,则过Po作椭圆的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是![]() ,那么对于双曲线则有如下命题: 若
,那么对于双曲线则有如下命题: 若![]() 在双曲线
在双曲线![]() (a>0,b>0)外
,则过Po作双曲线的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是
.
(a>0,b>0)外
,则过Po作双曲线的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是
.
3.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为5,那么
,公和为5,那么![]() 的值为________,这个数列的前n项和
的值为________,这个数列的前n项和![]() 的计算公式为_______
的计算公式为_______
4.若记号“*”表示两个实数a与b的算术平均的运算,即![]() ,则两边均含有运算符号“*”和“+”,且对于任意3个实数a,b,c都能成立的一个等式可以是______________。
,则两边均含有运算符号“*”和“+”,且对于任意3个实数a,b,c都能成立的一个等式可以是______________。
5.在平面上,设ha,hb,hc是三角形ABC三条边上的高.P为三角形内任一点,P到相应三边的距离分别为pa,pb,pc,我们可以得到结论: ![]() 试通过类比,写出在空间中的类似结论
试通过类比,写出在空间中的类似结论
(三)
1. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线
∥直线![]() ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为
2. 将演绎推理:![]() 在
在![]() 上是就减函数写成三段论的形式,其中大前提是
上是就减函数写成三段论的形式,其中大前提是
3.在△ABC中,![]() ,判断△ABC的形状并证明.
,判断△ABC的形状并证明.
4.在![]() DEF中有余弦定理:
DEF中有余弦定理:![]() . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱ABC-
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱ABC-![]() 的3个侧面面积与其中两个侧面所成二面角之间的关系式,并予以证明.
的3个侧面面积与其中两个侧面所成二面角之间的关系式,并予以证明.
(四)
1.已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.应假设
2.![]() 中,已知
中,已知![]() ,且
,且![]() ,求证:
,求证:![]() 为等边三角形。
为等边三角形。
3.证明:通过水管放水,当流速相同时,如果水管截面的周长相等,那么截面是圆的水管比截面是正方形的水管流量大![]()
4.△ABC三边长![]() 的倒数成等差数列,求证:角
的倒数成等差数列,求证:角![]()
![]() .
.
江苏省海门中学2008届高三数学每周天天练
(推理与证明预测答案)2008.3
班级 姓名 学号
(一)
1.设![]() ,
,![]()
![]() ,n∈N,则
,n∈N,则
![]()
答案:![]() ,由归纳推理可知其周期是4
,由归纳推理可知其周期是4
2.已知![]()
![]() ,猜想
,猜想![]() 的表达式为
的表达式为
答案:![]() ,由归纳推理可知:
,由归纳推理可知:![]() ,
,![]() ,
,![]()
3.如一个凸多面体是n棱锥,则这个凸多面体的所有顶点所确定的直线共有_____条,这些直线中共有![]() 对异面直线,则
对异面直线,则![]() ;f(n)=______(答案用数字或n的解析式表示)
;f(n)=______(答案用数字或n的解析式表示)
答案:![]() ;8;n(n-2)。
;8;n(n-2)。
解析:![]() ;
;![]() ;
;![]()
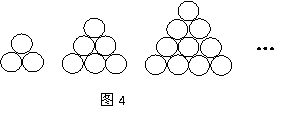 4.在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第
4.在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第![]() 堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第
堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第![]() 堆第
堆第![]() 层就放一个乒乓球,以
层就放一个乒乓球,以![]() 表示第
表示第![]() 堆的乒乓球总数,则
堆的乒乓球总数,则![]() ;
;![]() (答案用
(答案用![]() 表示)
表示)
答案:![]() 10,
10,![]()
 5.设平面内有
5.设平面内有![]() 条直线
条直线![]() ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用![]() 表示这
表示这![]() 条直线交点的个数,则
条直线交点的个数,则![]() =____________;当
=____________;当![]() 时,
时,![]() .(用
.(用![]() 表示)
表示)
答案:5,![]()
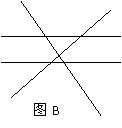
解:由图B可得![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,
![]() ,可推得
,可推得
∵n每增加1,则交点增加![]() 个,
个,
∴![]()
![]()
![]() .
.
(二)
1. ![]() ,观察以上两等式,请写出一个与以上两式规律相同的一个正确等式
,观察以上两等式,请写出一个与以上两式规律相同的一个正确等式
![]() (只要写出一个即可)
(只要写出一个即可)
2.若![]() 在椭圆
在椭圆![]() 外 ,则过Po作椭圆的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是
外 ,则过Po作椭圆的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是![]() ,那么对于双曲线则有如下命题: 若
,那么对于双曲线则有如下命题: 若![]() 在双曲线
在双曲线![]() (a>0,b>0)外
,则过Po作双曲线的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是
.
(a>0,b>0)外
,则过Po作双曲线的两条切线的切点为P1、P2,则切点弦P1P2的直线方程是
. ![]()
设![]() ,
,![]() ,
,![]() ,则过P1、P2的切线方程分别是
,则过P1、P2的切线方程分别是![]() ,
,
![]() .因为
.因为![]() 在这两条切线上,故有
在这两条切线上,故有![]() ,
,![]() ,这说明
,这说明![]() ,
,![]() 在直线
在直线![]() 上,故切点弦P1P2的直线方程是
上,故切点弦P1P2的直线方程是![]() .
.
3.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为5,那么
,公和为5,那么![]() 的值为_3__,这个数列的前n项和
的值为_3__,这个数列的前n项和![]() 的计算公式为_
的计算公式为_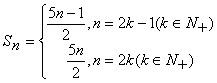 ____
____
4.若记号“*”表示两个实数a与b的算术平均的运算,即![]() ,则两边均含有运算符号“*”和“+”,且对于任意3个实数a,b,c都能成立的一个等式可以是_______________。
,则两边均含有运算符号“*”和“+”,且对于任意3个实数a,b,c都能成立的一个等式可以是_______________。
解析:由于本题是探索性和开放性问题,问题的解决需要经过一定的探索过程,并且答案不惟一。这题要把握住![]() ,还要注意到试题的要求不仅类比推广到三个数,而且等式两边均含有运算符号“*”和“+”,则可容易得到a+(b
,还要注意到试题的要求不仅类比推广到三个数,而且等式两边均含有运算符号“*”和“+”,则可容易得到a+(b![]() c)=(a+b)
c)=(a+b)![]() (a+c)。正确的结论还有:(a
(a+c)。正确的结论还有:(a![]() b)+c=(a
b)+c=(a![]() c)+(b
c)+(b![]() c),(a
c),(a![]() b)+c=(b
b)+c=(b![]() a)+c等。
a)+c等。
5. 在平面上,设ha,hb,hc是三角形ABC三条边上的高.P为三角形内任一点,P到相应三边的距离分别为pa,pb,pc,我们可以得到结论: ![]() 试通过类比,写出在空间中的类似结论 设ha,hb,hc,
试通过类比,写出在空间中的类似结论 设ha,hb,hc,![]() 三棱锥A-BCD四个面上的高.P为三棱锥A-BCD内任一点,P到相应四个面的距离分别为pa,pb,pc,
三棱锥A-BCD四个面上的高.P为三棱锥A-BCD内任一点,P到相应四个面的距离分别为pa,pb,pc,
![]() 我们可以得到结论:
我们可以得到结论: ![]()
(三)
1. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线
∥直线![]() ”的结论显然是错误的,这是因为 大前提是错误的
”的结论显然是错误的,这是因为 大前提是错误的
2. 将演绎推理:![]() 在
在![]() 上是减函数写成三段论的形式,其中大前提是
上是减函数写成三段论的形式,其中大前提是
若![]() ,则函数
,则函数![]() 在
在![]() 上是减函数
上是减函数
3.在△ABC中,![]() ,判断△ABC的形状并证明.
,判断△ABC的形状并证明.
分析:![]()
![]()
![]()
![]()
所以三角形ABC是直角三角形
4.在![]() DEF中有余弦定理:
DEF中有余弦定理:![]() . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱ABC-
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱ABC-![]() 的3个侧面面积与其中两个侧面所成二面角之间的关系式,并予以证明.
的3个侧面面积与其中两个侧面所成二面角之间的关系式,并予以证明.
分析 根据类比猜想得出![]() .
.
其中![]() 为侧面为
为侧面为![]() 与
与![]() 所成的二面角的平面角.
所成的二面角的平面角.
证明: 作斜三棱柱![]() 的直截面DEF,则
的直截面DEF,则![]() 为面
为面![]() 与面
与面![]() 所成角,在
所成角,在![]() 中有余弦定理:
中有余弦定理:
![]() ,
,
同乘以![]() ,得
,得
![]()
即 ![]()
评注 本题考查由平面三角形的余弦定理到空间斜三棱柱的拓展推广,因为类比是数学发现的重要源泉,因此平时的教学与复习中更要注意类比等思想方法的学习。
(四)
1.已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根.应假设 三个方程中都没有两个相异实根
证明:假设三个方程中都没有两个相异实根,
则Δ1=4b2-4ac≤0,Δ2=4c2-4ab≤0,Δ3=4a2-4bc≤0.
相加有a2-2ab+b2+b2-2bc+c2+c2-2ac+a2≤0,
(a-b)2+(b-c)2+(c-a)2≤0. ①
由题意a、b、c互不相等,∴①式不能成立.
∴假设不成立,即三个方程中至少有一个方程有两个相异实根.
方法总结:反证法步骤—假设结论不成立→推出矛盾→假设不成立![]()
凡是“至少”、“唯一”或含有否定词的命题适宜用反证法![]()
2.![]() 中,已知
中,已知![]() ,且
,且![]() ,求证:
,求证:![]() 为等边三角形。
为等边三角形。
分析:由![]()
由![]()
![]()
所以![]() 为等边三角形
为等边三角形
3.证明:通过水管放水,当流速相同时,如果水管截面的周长相等,那么截面是圆的水管比截面是正方形的水管流量大![]()
分析:当水的流速相同时,水管的流量取决于水管截面面积的大小,设截面的周长为L,则周长为L的圆的半径为![]() ,截面积为
,截面积为![]() ;周长为L的正方形边长为
;周长为L的正方形边长为![]() ,截面积为
,截面积为![]()
![]() 所以本题只需证明
所以本题只需证明![]()
![]()
证明:设截面的周长为L,依题意,截面是圆的水管的截面面积为![]() ,截面是正方形的水管的截面面积为
,截面是正方形的水管的截面面积为![]() ,所以本题只需证明
,所以本题只需证明![]()
为了证明上式成立,只需证明 ![]()
两边同乘以正数![]() ,得
,得![]()
因此,只需证明![]()
上式是成立的,所以![]()
这就证明了,通过水管放水,当流速相同时,如果水管截面的周长相等,那么截面是圆的水管比截面是正方形的水管流量大![]()
说明:对于较复杂的不等式,直接运用综合法往往不易入手,因此,通常用分析法探索证题途径,然后用综合法加以证明,所以分析法和综合法经常是结合在一起使用的![]()
4.△ABC三边长![]() 的倒数成等差数列,求证:角
的倒数成等差数列,求证:角![]()
![]() .
.
分析:因为![]() ,
,
故要证明角![]()
![]() 即
即![]()
只需证![]()
又三边长![]() 的倒数成等差数列即
的倒数成等差数列即![]()
只需证![]()
即![]()
又![]()
只需证![]()
即证:![]()
而上式显然成立
所以角![]()
![]()
注意:本题也可用反证法