高考理科数学月考试卷（六）
时量：120分钟 满分：150分
得分：
一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．直线
按向量
的平移后，得到的直线方程为
A．
B．
C．
D．
2．已知集合
，则
A．{（0，1），（1，3）} B．R
C．（0，+∞） D．[
）
3．函数
的反函数
的一个单调减区间是
A．（
） B．（
） C．（
） D．（
）
4．数列{an}满足
A．2 B．－
C．－
D．1
5．代数式
的展开式中，含
项的系数是
A．－30 B．30 C．70 D．90
6．△ABC中，已知：sinA：sinB：sinC=1:1:
，且S△ABC=
，则
的值是
A．2 B． C．－2 D．－
7．若函数
满足：“对于区间（1，2）上的任意实数
，
恒成立，”则称为完美函数.在下列四个函数中，完美函数是
A．
B．
C．
D．
8．将4个相同的白球和5个相同的黑球全部放入3个不同的盒子中，每个盒子既要有白球，又要有黑球，且每个盒子中都不能同时只放入2个白球和2个黑球，则所有不同的放法种数为
A．3 B．6 C．12 D．18
9．设双曲线
（b＞a＞0）的半焦距为c，直线l过A（a,0）,B(0,b)两点，若原点O到l的距离为
，则双曲线的离心率为
A．
或2 B．2 C．
D．
10．对于任意的两个实数对（a,b）和（c,d），规定当且仅当
时(a,b)=(c,d)；现定义两种运算，运算“
”为：（a,b）（c,d）=（
）；运算“
”为：(a,b) (c,d)=（
）.设
、
.若（1，2）
=（5,0）.则（1，2）=
A．（4,0） B．（2,0） C．（0，2） D．（0，－4）
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 得分 |
| 答案 |
二、填空题（本大题共5小题，每小题5分，共25分，把答案填写在答题卷中对应题号后的横线上）
11．
的值为
。
12．设直线
与圆
相交于A、B两点，且弦长为
，则a=
。
13．已知：点P的坐标（
）满足：
（O为坐标原点）的最大值是
。
14．关于x的不等式：
至少有一个负数解，则a的取值范围是
。
15．已知：是定义的R上的不恒为零的函数，且对任意a、b
，满足：
，且
=
；数列{an}的通项公式an=
。
三、解答题（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤）
16．（本小题满分12分）
已知函数
的最小正周期为
，且当
时，函数取最大值.
（1）求的解析式；
（2）试列表描点作出在[0，]范围内的图象.
17．（本小题满分12分）
国家射击队为备战2008年北京奥运会进行紧张艰苦的训练，训练项目完成后，教练总会设计安排一些放松、娱乐性恢复活动。在一次速射“飞碟”的游戏活动中，教练制定如下规则：每次飞碟飞行过程中只允许射击三次，根据飞碟飞行的规律，队员甲在飞行距离为50米远处命中的概率为
.
（1）如果队员甲一共参加了三次射击飞碟的游戏，试求队员甲在这三次游戏中第一枪至少有一次击中的概率。
（2）如果队员甲射击飞行距离为50米远处的飞碟，如果第一次未命中，则进行第二次射击，同时第二次射击时飞碟行距离变为100米；如果第二次未命中，则进行第三次射击，第三次射击时飞碟飞行距离变为150米（此后飞碟不在射程之内）.已知，命中的概率与飞碟飞和地距离的平方成反比.求队员甲在一次游戏中命中飞碟的概率。
18．（本小题共12分）
在直三棱柱
中，A1A=AB=3，AC=3，
、Q分别为棱BB1、CC1上的点，且
.
（1）求平面APQ与面ABC所成的锐二面角的大小.
（2）在线段A1B（不包括两端点）上是否存在一点M，使AM+MC1最小？
若存在，求出最小值；若不存在，说明理由.
19．（本小题满分13分）
已知圆M：（x+
）2+y2=36及定点N（，0），点P是圆M上的动点，点Q在NP上，点G在MP上，且满足
.
（1）求点G的轨迹C的方程.
（2）过点K（2，0）作直线l，与曲线C交于A、B两点，O是坐标原点，设
，是否存在这样的直线
，使四边形OASB的对角线相等？若存在，求出直线的方程；若不存在，说明理由.
20．（本小题满分13分）
某加工厂有一块三角形的铁板余料（如图），经测量得知：AC=3，AB=3
，BC=6.工人师傅计划用它加工成一个无盖直三棱柱型水箱，设计方案为：将图中的阴影部分切去，再把它沿虚线折起，请计算容器的高为多少时，容器的容积最大？最大容积是多少？
 |
21．（本小题满分13分）
数列
，由下列条件确定：①a1＜0，b1＜0.②当k≥2时，ak和bk满足下列条件：当
.
（1）若
，
，分别写出{an}、{bn}的前四项.
（2）证明数列{ak－bk}是等比数列.
（3）设
是满足b1＞b2＞…＞bn的最大整数时，用a1、b1表示n满足的条件.
参考答案
一、选择题
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | D | D | C | A | A | C | A | C | B | B |
二、填空题
11．
12.
0 13. 5 14. (
) 15.
三、解答题
16．解：（1）
……………（4分）
∵的周期为，∴
.
1°当
=1时，
是函数的最大值，
……………………………………（5分）
2°当=－1时，
不是函数的最大值. 
（舍去）…………………………（7分）
∴
…………………………………………………………………（8分）
（2）
|
| 0 |
|
|
|
|
|
|
|
|
|
| 2 |
|
| 0 |
|
作图如下.
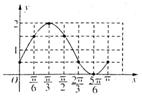……………………………………………………………………（12分）
17．解：（1）记“队员甲在三次游戏中，第一枪至少有一次命中”为事件A.
……………………………………………………………………（5分）
（2）记在一次游戏中“第i次击中飞碟”为事件
…………………………（8分）
又
是相互独立事件.
………………………………………………………（12分）
18．解：（1）建立如图所示空间直角坐标系A
A（0，0，0），P（3，0，），Q（0，3，2）.
设平面APQ的一个法向量为
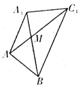令
，则
平面ABC的一个法向量
∴平面APQ与面ABC所成的锐角大小为45°.…………………………………………（6分）
（1）问也用传统方法求解.（并参照计分）
（2）沿A1B将面A1BC1与面A1BA展开，连结AC1与A1B交于点M，此时AM+MC1有最小值.
∵
又C1A1⊥面ABB1A1，∴C1A1⊥A1B.
∴△AA1C1中，∠AA1C1=135°
AC1=
∴存在点M，使AM+AC1取最小值为
……………………………………………（12分）
19．解：（1）
为PN的中点，且GQ
是PN的中垂线.
∴
又
∴点G的轨迹是以M、N为焦点的椭圆，
∴
的轨迹方程是
……………………………………（5分）
（2）
四边形OASB为平行四边形，假设存在直线，使
；则四边形OASB为矩形.
若直线的斜率不存在，则的方程为
.
，这与
=0矛盾，故的斜率存在.………………………（7分）
设直线的方程为
、
.
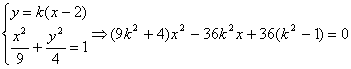………………………（9分）
又
………………………（12分）
∴存在直线
满足条件. …………………………（13分）
20．解：设容器的高为x.
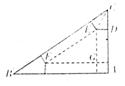
又GE＞0，∴0＜x＜
设容器的容积为V.
则V=
…………………………………………………………（6分）
……………………………………………………（7分）
令
，又0＜x＜
………………………………（10分）
当0＜x＜
时，
.……………………………………………………（13分）
21．解：（1）
………………………………………………………………………（3分）
（2）当
时，
当
时，
又
，∴数列
是等比数列. ……………………………………………（9分）
（3）当b1＞b2＞…＞bn（n≥2）时，bk≠bk-1(2≤k≤n).
由（2）知：
不成立，
.
从而对于2≤k≤n有ak=ak-1,bk=
于是
……………………………………………………………………（11分）
若
，则
这与
是满足b1＞b2＞…＞bn（n≥2）的最大整数矛盾.
∴n是满足
的最小整数.
n是满足大于
的最小整数.…………………………（13分）