08高考文科数学四校质量调研试卷 2008.2
命题、审核:冯淑平 校对:____________
考生注意:
1.答题前,考生务必用钢笔或圆珠笔清楚填写班级、姓名和学号。
2.本试卷共有22试题,答案直接写在试卷上。
3.本试卷共6页。考试时间120分钟。试卷满分150分。
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | |||||||||

一、填空题(本大题共12题,每小题4分,共48分)
1.![]() ___________.
___________.
2已知函数![]()
![]() ,则
,则![]() __________.
__________.
3.集合A=![]() ,集合B=
,集合B=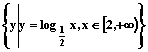 ,则
,则![]() ______________.
______________.
4.过点![]() 作曲线
作曲线![]() 的切线,则所作切线的一般式方程为___________________________.
的切线,则所作切线的一般式方程为___________________________.
5.在![]() 中,角
中,角![]() 所对应的边分别为
所对应的边分别为![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积为___________.
的面积为___________.
6.方程![]() 的解是____________.
的解是____________.
7.设等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() 前n项和为
前n项和为![]() ,若
,若![]() ,则
,则![]() 的值为________.
的值为________.
8.在![]() 中,
中,![]() 为直角,设P为
为直角,设P为![]() 内一点,且
内一点,且![]() ,则
,则![]() 的面积与
的面积与![]() 的面积之比为_______.
的面积之比为_______.
9.为了参与上海世博会的建设,某外商计划在4个候选区县投资3个不同的项目,且在同一个区县投资的项目不超过2个,该外商不同的投资方案有______种.
10.如果函数![]() 在区间
在区间![]() 上是减函数,那么实数a的取值范围是_________.
上是减函数,那么实数a的取值范围是_________.
11.在平面直角坐标系中,命题“若直线l过抛物线![]() 的焦点,且与抛物线相交于
的焦点,且与抛物线相交于![]() 两点,则
两点,则![]() ”为真命题,如果直线l不是经过抛物线
”为真命题,如果直线l不是经过抛物线![]()
![]() 的焦点而是经过x轴上另外一个定点
的焦点而是经过x轴上另外一个定点![]()
![]() ,并且保证直线与抛物线有两个公共点,那么
,并且保证直线与抛物线有两个公共点,那么![]() 是否还是定值吗?请作出肯定或否定的回答,并且写出
是否还是定值吗?请作出肯定或否定的回答,并且写出![]() 的表达式____________________________________________.
的表达式____________________________________________.
12.(文科)设方程![]() 的两个根为
的两个根为![]() ,则
,则![]() 与1的大小关系为___________.
与1的大小关系为___________.

二、选择题(本大题共4题,每小题4分,共16分)
13.在等比数列![]() 中,
中,![]() ,且
,且![]() ,则
,则![]() 的值为
( )
的值为
( )
(A)![]() (B)-5 (C)5
(D)8
(B)-5 (C)5
(D)8
14.“![]() ”是“
”是“![]() ”的
( )
”的
( )
(A)充分非必要条件 (B)必要非充分条件
(C)充要条件 (D)非充分非必要条件
15.已知P是椭圆![]() 上的点,
上的点,![]() 是两个焦点,则
是两个焦点,则![]() 的最大值与最小值之差是
( )
的最大值与最小值之差是
( )
(A)1 (B)2 (C)3 (D)4
16.设S是至少含有两个元素的集合.在S上定义了一个二元运算“*”(即对任意的![]() ,对于有序元素对
,对于有序元素对![]() ,在S中有唯一确定的元素
,在S中有唯一确定的元素![]() *
*![]() 与之对应)。若对任意的
与之对应)。若对任意的![]() ,有
,有![]() *
*![]()
![]() *
*![]()
![]() =
=![]() ,则对任意的
,则对任意的![]() ,下列等式中不恒成立的是
( )
,下列等式中不恒成立的是
( )
(A)![]() *
*![]()
![]() *
*![]()
![]() =
=![]() (B)
(B)![]()
![]() *
*![]()
![]() *
*![]() =
=![]()
(C)![]() *
*![]()
![]() *
*![]()
![]()
![]() *
*![]()
![]() *
*![]()
![]() =
=![]() (D)
(D)![]()
![]() *
*![]()
![]() *
*![]() *
*![]()
![]() *
*![]()
![]()
![]() =
=![]()

三、解答题(本大题共6题,第17题10分,第18题12分,第19、20题每 题 14分,第21、22题18分,共86分.)
17.设复数![]() ,且复数
,且复数![]() 满足
满足![]() (i为虚数单位),则当
(i为虚数单位),则当![]() 满足什么条件时,
满足什么条件时,![]() 是纯虚数.
是纯虚数.
18.已知函数![]() (其中
(其中![]() ),
),![]() .若函数
.若函数![]() 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为![]() ,且直线
,且直线![]() 是函数
是函数![]() 图像的一条对称轴.
图像的一条对称轴.
(1)求![]() 的表达式.
的表达式.
(2)求函数![]() 的单调递增区间.
的单调递增区间.
19.一长方形泳池中相邻的两条泳道![]() 和
和![]() (看成两条互相平行的线段)分别长90米,甲在泳道
(看成两条互相平行的线段)分别长90米,甲在泳道![]() 上从
上从![]() 处出发,以3米/秒的速度到达
处出发,以3米/秒的速度到达![]() 以同样的速度返回
以同样的速度返回![]() 处,然后重复上述过程;乙在泳道
处,然后重复上述过程;乙在泳道![]() 上从
上从![]() 处出发,以2米/秒的速度到达
处出发,以2米/秒的速度到达![]() 以同样的速度游回
以同样的速度游回![]() 处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
处,然后重复上述过程.(不考虑每次折返时的减速和转向时间).两人同时开始运动.
 (1)设甲离开池边
(1)设甲离开池边![]() 处的距离为y米,当时间
处的距离为y米,当时间![]() (单位:
(单位:
秒)时,写出y关于t的函数解析式.
(2)在右图的直角坐标系中,x轴表示时间![]() (单位:秒),
(单位:秒),
y轴表示离开池边![]() 处的距离.在同一个坐标系中画出
处的距离.在同一个坐标系中画出
甲乙两人各自运动的函数图像.(实线表示甲的图像,虚线表示乙的图像).
 (3)请根据图像判断从开始运动起到3分钟为止,甲乙的相遇次数.
(3)请根据图像判断从开始运动起到3分钟为止,甲乙的相遇次数.

 20.设A,B分别是双曲线
20.设A,B分别是双曲线![]()
![]() 的左右顶点,双曲线的实轴长为
的左右顶点,双曲线的实轴长为![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求此双曲线的方程.
(2)已知直线![]() 与双曲线的右支交于
与双曲线的右支交于![]() 两点,且在双曲线的右支上存在点
两点,且在双曲线的右支上存在点![]() ,使得
,使得![]() ,求
,求![]() 的值及点
的值及点![]() 的坐标.
的坐标.
 21.(文科)在数列
21.(文科)在数列![]() (n
(n![]() )中,当n为奇数时,
)中,当n为奇数时,![]() ,当n为偶数时,
,当n为偶数时,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() .
.
(2)令![]() ,(n
,(n![]() ,判断数列
,判断数列![]() 是否为等差数列,并证明你的结论.
是否为等差数列,并证明你的结论.
(3)求![]() .
.
22.(文科)设集合P=![]()
(1)试判断![]() ;
;![]() ,是否属于集合P?
,是否属于集合P?
(2)若![]()
![]() 属于P,试寻找其充要条件.
属于P,试寻找其充要条件.
(3)根据对第(1),(2)小题的研究,请你对属于集合P的函数从函数性质方面提出一个有价值的结论,说明理由;若![]()
![]() ,利用研究所得的结论判断
,利用研究所得的结论判断![]() 与集合P的关系.
与集合P的关系.
答案:
一.1. ![]() 2.
2. ![]() 3. (-2,-1] 4.
3. (-2,-1] 4. ![]() 5.
5. ![]() 6. x=10 7. 0
6. x=10 7. 0
8.![]() 9. 60 10. [-3,-2] 11.
是定值,
9. 60 10. [-3,-2] 11.
是定值, ![]() 12.(文)
12.(文) ![]()
(理)
![]()
二.13. C 14. B 15. A 16. B
三.17.![]() (3分
(3分
![]() (5分)
(5分)
若![]() 是纯虚数,则
是纯虚数,则![]() ,
(8分)
,
(8分)
即当![]() 时,
时, ![]() 是纯虚数.
(10分)
是纯虚数.
(10分)
18.(1)由函数![]() 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为![]() 得函数周期为
得函数周期为![]() ,
,
![]() (2分)
(2分)
![]() 直线
直线![]() 是函数
是函数![]() 图像的一条对称轴,
图像的一条对称轴,![]() ,
(4分)
,
(4分)
![]() 或
或![]() ,
,![]() ,
, ![]() ,
, ![]() .
(6分)
.
(6分)
![]() .
(7分)
.
(7分)
(2)![]()
![]() (10分)
(10分)
![]() ,
,
即函数![]() 的单调递增区间为
的单调递增区间为![]() .
(12分)
.
(12分)
 19.(1)
19.(1)![]() (5分)
(5分)
(2)如右图.(说明:若写出乙的函数解析式,则
给予相应的得分) (11分)
![]() (3)五次.
(14分)
(3)五次.
(14分)
20.(1)由双曲线的实轴长为![]() 得
得![]() .
(2分)
.
(2分)
双曲线右焦点的坐标为![]() ,一条渐进线为
,一条渐进线为![]() ,由点到直线的距离公式得
,由点到直线的距离公式得![]() ,
,
双曲线的方程为![]() .
(5分)
.
(5分)
(2)设![]()
将直线![]() 代入双曲线方程,化简得
代入双曲线方程,化简得![]() ,
(7分)
,
(7分)
![]() .
.
![]() ,
,![]() .
(11分)
.
(11分)
将点![]() 的左边代入双曲线的方程
的左边代入双曲线的方程![]() ,解得
,解得![]() .
(13分)
.
(13分)
当![]() 时,点
时,点![]() 在已知双曲线的左支上,不合题意,舍去.
在已知双曲线的左支上,不合题意,舍去.
得![]() ,点
,点![]() 的坐标为
的坐标为![]() (14分)
(14分)
21.(文科)
(1)![]() .
(4分)
.
(4分)
(2)![]() (5分)
(5分)
![]()
![]() 是奇数,
是奇数,![]()
![]() (7分)
(7分)
![]()
![]() 是偶数,
是偶数,![]()
![]() ,
(9分)
,
(9分)
![]() 即
即![]() ,
,
![]() 数列
数列![]() 是首项为2,公差为4的等差数列.
(12分)
是首项为2,公差为4的等差数列.
(12分)
(3)![]() ,
(13分)
,
(13分)
![]() (15)分
(15)分
![]()
![]()
![]() (18分)
(18分)
(理科)
(1)若![]() 时,
时,![]() ,
,![]() .
(3分)
.
(3分)
任取![]()
![]() ,
,![]() (7分)
(7分)
(2)若![]() 则
则![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() 对任意的
对任意的![]() 恒成立,
恒成立,![]() (11分)
(11分)
(3)可得对属于集合P的函数是奇函数.
取![]() .
(13分)
.
(13分)
任取![]() 令
令![]() ,得
,得![]() ,
,
得![]() ,
, ![]()
![]() 对属于集合P的函数必是奇函数.
(16分)
对属于集合P的函数必是奇函数.
(16分)
因为如果一个函数不是奇函数,则此函数不属于集合P,而二次函数![]()
![]() 必定不是奇函数,所以
必定不是奇函数,所以![]()
![]()
![]() . (18分)
. (18分)
22.(文科)
同理科21题.
(理科)
(1)![]() .
(2分)
.
(2分)
(2)![]() (3分)
(3分)
![]()
![]() 是奇数,
是奇数,![]()
![]()
![]()
![]() 是偶数,
是偶数,![]()
![]() ,
(7分)
,
(7分)
![]() 即
即![]() ,
,
![]() 数列
数列![]() 是首项为2,公差为4的等差数列.
(8分)
是首项为2,公差为4的等差数列.
(8分)
![]()
![]() ,
, ![]() ,
, ![]() 当
当![]()
![]() 为奇数时,
为奇数时,![]() .
.
当![]()
![]() 为偶数时,
为偶数时,![]() .
.
![]() .
(12分)
.
(12分)
(3)![]() ,
, ![]() ,
(14分)
,
(14分)
![]() ,
,
![]()
![]() (16分)
(16分)
![]() =
=![]()
![]()
![]() (18分)
(18分)