08届高三数学第一学期期末考试试题
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.若![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在等差数列![]() 中,若
中,若![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,则
项和,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.用![]() 表示一个平面,
表示一个平面,![]() 表示一条直线,则
表示一条直线,则![]() 内至少有一条直线与
内至少有一条直线与![]() ( )
( )
A.平行 B.相交 C.垂直 D.异面
5.若![]() ,则
,则![]() 为
( )
为
( )
A.锐角三角形 B.钝角三角形
C.等腰直角三角形 D.直角三角形
6.![]() 是直线
是直线![]() 和直线
和直线![]() 互相垂直的 ( )
互相垂直的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.一动圆圆心在抛物线![]() 上,过点
上,过点![]() 且恒与定直线
且恒与定直线![]() 相切,则直线
相切,则直线![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)已知![]() ,函数
,函数![]() 在
在![]() 上是单调增函数,则
上是单调增函数,则![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.若函数![]() 对任意的实数
对任意的实数![]() 都有
都有![]() ,则
,则![]()
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.设![]() 且
且![]() ,则下列关系式一定成立的是( )
,则下列关系式一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
|
二、填空题(本大题共4小题,每小题4分,共16分)
A.![]() B.
B.![]() C.
C.![]() D.
D.
13.设![]() ,则
,则![]() 这四个数由小到大的顺序为
这四个数由小到大的顺序为
14.设![]() ,式中变量
,式中变量![]() 满足下列条件:
满足下列条件: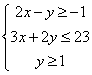 ,则
,则![]() 的最大值为
的最大值为
15.(理)![]()
(文)若曲线![]() 与直线
与直线![]() 没有公共点,则
没有公共点,则![]() 的取值范围是
的取值范围是
16.定义![]() 为
为![]() 和
和![]() 中的较大者,当
中的较大者,当![]() 时,
时,![]() 的最小值为
的最小值为
三、解答题(本大题共6小题,前五题每小题12分,22题14分,共74分)
17.设![]() 、
、![]() 是两个垂直的单位向量,且
是两个垂直的单位向量,且![]() ,
,![]() ,
,
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值。
的值。
18.已知函数![]() ,
,![]() ,且
,且![]() 的最大值为
的最大值为![]() ,其图象相邻两对称轴间的距离为
,其图象相邻两对称轴间的距离为![]() ,并过点
,并过点![]() ,
,
(1)求![]() ;
;
(2)计算![]() 。
。
19.如图,在四棱椎![]() 中,底面为直角梯形,且
中,底面为直角梯形,且![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() 分别为
分别为![]() 的中点。
的中点。
(1)求证:![]() ;
;
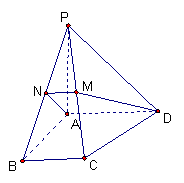 (2)求
(2)求![]() 与平面
与平面![]() 所成的角。
所成的角。
20.(理)已知函数![]() ,
,
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() ,证明:
,证明:![]() 。
。
(文)已知![]() 在
在![]() 取得极值,且
取得极值,且![]() ,
,
(1)试求常数![]() 的值;
的值;
(2)试判断![]() 是函数的极大值还是极小值,并说明理由。
是函数的极大值还是极小值,并说明理由。
 21.如图,椭圆
21.如图,椭圆![]() 与过点
与过点![]() 的直线有且只有一个公共点
的直线有且只有一个公共点![]() ,且椭圆的离心率
,且椭圆的离心率![]()
(1)求椭圆的方程;
(2)设![]() 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点,
求证:![]() 。
。
22.数列![]() 满足递推式
满足递推式![]() ,其中
,其中![]() ,
,
(1)求![]() ;
;
(2)若存在一个实数![]() ,使得
,使得![]() 为等差数列,求
为等差数列,求![]() 值;
值;
(3)(理)求数列![]() 的前
的前![]() 项之和。
项之和。
参考答案
第I卷(选择题,共60分)
|
1.D 2.B 3.C 4.C 5.D 6.A 7.B 8.A 9.B 10.(理)A 文(D)
11.D 12.C
第II卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分)
13.![]() 14.11
14.11
15.(理)![]() (文)[—1,1] 16.—
(文)[—1,1] 16.—![]()
三、解答题(本大题共6小题,前五题每小题12分,22题14分,共74分)
17.解:(1)![]()
∴存在实数k,解得![]()

(2)由已知![]()
![]()

![]()
18.解:(1)![]()

|

19.证明:(1)∵N是PB的中点
PA=PB ∴AN⊥PB
∵AD⊥平面PAB, ∴AD⊥PB
从而PB⊥平面ADMN
∵DM![]() 平面ADMN
平面ADMN
∴PB⊥DM
解:(2)取AD中点为G,连结BG,NG,则BG//CD
∴BG与平面ADMN所成的角和CD与平面ADMN所成的角相等
∵PB⊥平面ADMN
∴∠BGN是BG与平面ADMN所成的角
在Rt△BGN中,![]()
故CD与平面ADMN所成的角是![]()
20.解:(理)(1)由题意,得x+1>0,x>—1

(2)由(1)![]()

(文)(1)![]()
(2)![]() ,
,
当![]() 有极小值。
有极小值。
|
由题意得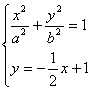 有唯一解
有唯一解

从而得![]() ,
,
故所求的椭圆方程为![]()
(2)由(1)得![]()

22.解:(1)由![]() ,知
,知
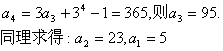
(2)![]()
![]()
(3)由(2)得
![]()
先求![]()

由上两式相减


