08届高三理科数学第一学期期末考试
理科数学
一、选择题(共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.
下列函数中,最小正周期为![]() 的是 ( )
的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.
已知等差数列![]() 的公差为2, 若
的公差为2, 若![]() 成等比数列, 则
成等比数列, 则![]() =( )
=( )
A . –4 B. –6 C. –8 D. –10
3.
已知函数![]() 是
是![]() 的反函数,若
的反函数,若![]() 的图象过点(3,4),则
的图象过点(3,4),则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
4.
若![]() 为虚数单位,则复数
为虚数单位,则复数![]() 在复平面内对应的点在 ( )
在复平面内对应的点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.
(2x3-![]() )7的展开式中常数项是( )
)7的展开式中常数项是( )
A![]() 14 B
14 B![]() -14 C
-14 C![]() 42 D
42 D![]() -42
-42
6. 设集合A={xx2<a} ,B={xx<2},若A∩B=A, 则实数a的取值范围是( )
A.a<4 B.a£4 C. 0<a£4 D. 0<a<4
7.
设抛物线![]() 与过其焦点的直线交于
与过其焦点的直线交于![]() 两点,则
两点,则![]() 的值
的值
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
8. 已知![]() =(2,3),
=(2,3),![]() =(-4,7),则
=(-4,7),则![]() 在
在![]() 方向上的投影为( )
方向上的投影为( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]()
D
D![]()
![]()
9.
P为椭圆![]() 上的点,
上的点,![]() 是两焦点,若
是两焦点,若![]() ,则
,则![]() 的面积是(
)
的面积是(
)
A.![]() B.
B.![]() C.
C.![]() D.
16
D.
16
10. 在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
11.
若关于x的方程x2-x+a=0和x2-x+b=0(a![]() )的四个根可以组成首项为
)的四个根可以组成首项为![]() 的等差数列,则a+b的值为( )
的等差数列,则a+b的值为( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
12.定义行列式运算![]() =
=![]() .将函数
.将函数![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位,所得图象对应的函数为偶函数,则
)个单位,所得图象对应的函数为偶函数,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共4小题,每小题5分,共20分.
13. 函数![]() 的定义域为 .
的定义域为 .
14. 过长方体的同一个顶点的三条棱长为3cm、4cm、5cm,且它的八个顶点都在一个球面上,这个球的表面积是 cm2.
15. 若椭圆![]() 的离心率为
的离心率为![]() ,则双曲线
,则双曲线![]() 的离心率为_______
的离心率为_______
16.
定义“符号函数”f(x)=sgnx=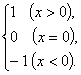
则不等式x+2>(x-2)sgnx的解集是___________.
高三理科数学答题卡
座位号
一. 选择题 : 本大题共12小题, 每小题5分, 共60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二.填空题: 本大题有4小题, 每小题5分, 共20分.
13. 14.
15. 16.
三、解答题:本大题共6小题,第17题10分,18-22题各12分,共70分.
解答应写出文字说明,证明过程或演算步骤.
17. ![]() 中,
中,![]() ,求
,求![]() 的值和
的值和![]() 的面积.
的面积.
18.
一个袋子中有4个红球和3个黑球,现从该袋中取出4个球,规定取到一个红球得3分,取到一个黑球得1分,记所取球的得分为![]() .
.
(Ⅰ)求![]()
![]() 的概率;
的概率;
(Ⅱ) 求随机变量![]() 的数学期望
的数学期望![]() .
.
19. △OAB是边长为4的正三角形,CO⊥平面OAB且CO=2,设D、E分别是OA、AB的中点。
(Ⅰ)求证:OB∥平面CDE;
(Ⅱ)求二面角O-DE-C的大小。
 |
20.
已知函数![]() 在
在![]() 处取得极值2.
处取得极值2.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)直线![]() 与
与![]() 的图象相切于点P
的图象相切于点P![]() ,求直线
,求直线![]() 的方程.
的方程.
(Ⅲ)m满足什么条件时,函数![]() 在区间
在区间![]() 上单调递增?
上单调递增?
21.
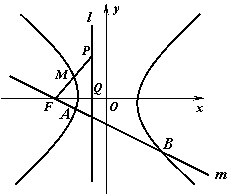
如图,点![]()
![]() 为双曲线
为双曲线![]() :
: ![]() (
(![]() ,
,![]() )的左焦点,左准线
)的左焦点,左准线![]() 交
交![]() 轴于点
轴于点![]() ,点P是
,点P是![]() 上的一点,已知
上的一点,已知![]() ,且线段PF的中点
,且线段PF的中点![]() 在双曲线
在双曲线![]() 的左支上.
的左支上.
(Ⅰ)给出b和c 的关系式,并用c表示点M的坐标;
(Ⅱ)求双曲线![]() 的标准方程;
的标准方程;
(Ⅲ)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左右两支分别交于
的左右两支分别交于![]() 、
、![]() 两点,
两点,
设![]() ,当
,当![]() 时,求直线
时,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
 |
22. 已知![]() ,
,![]() . 数列
. 数列![]() 满足
满足![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)已知![]() ≥
≥![]() ,证明:
,证明:![]() ;
;
(Ⅲ)设![]() 是数列
是数列![]() 的前
的前![]() 项和,判断
项和,判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
高三数学参考答案及评分标准
一、选择题(本大题共12个小题,每小题5分,共60分. )
1.B 2. B 3. D 4. D / C 5. A 6.B 7. B 8. C 9. B 10. B 11. C 12. B
二、填空题(本大题共4个小题,每小题5分,共20分. )
13. ![]() 14. 50π 15.
14. 50π 15. ![]() 16. (-
16. (-![]() ,+∞)
,+∞)
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。)
17.解:![]()
![]() ,
,
所以![]() ,
,
![]() 。
。
18.解:(Ⅰ)![]()
![]() 时,这四个球中有1个红球,3个黑球………………………..2分
时,这四个球中有1个红球,3个黑球………………………..2分
![]() ……………………………………………………….4分
……………………………………………………….4分
(Ⅱ)随机变量![]() 的可能取值有:6、8、10、12,
的可能取值有:6、8、10、12,
![]() , ,
, ,![]()
![]() ,
,![]() …………7分
…………7分
|
| 6 | 8 | 10 | 12 |
|
|
|
|
|
|
故随机变量![]() 概率分布列是:
概率分布列是:
…….………………………8分
![]() …………………………………11分
…………………………………11分
答: (Ⅰ)
当![]()
![]() 时的概率为
时的概率为![]() ;
;
(Ⅱ)随机变量![]() 的数学期望
的数学期望![]() 为
为![]() .……12分
.……12分
 19. 解:(1)证明:∵DE是△AOB的中位线
19. 解:(1)证明:∵DE是△AOB的中位线
∴DE∥OB
DE![]() 平面CDE
平面CDE
OB![]() 平面CDE
平面CDE
∴OB∥平面CDE
(2)解法一:
作OM⊥直线DE于M点,
∵CO⊥平面OAB,由三垂线定理CM⊥DE,作OH⊥CM于H
则OH⊥相交直线CM、ME,∴OH⊥平面CDE
已证OM,CM都垂直于DE,∴∠OMC是二面角O-DE-E的平面角 ,
cos∠OMC=![]() =
=![]() =
=![]() ,∴二面角O—DE-C的大小为arccos
,∴二面角O—DE-C的大小为arccos![]()
解法二:
如图,以O为原点,![]() 为z轴正向,
为z轴正向,![]() 为y轴正向,在平面OAB内作OF⊥y轴并以
为y轴正向,在平面OAB内作OF⊥y轴并以![]() 为x轴正向建立空间直角坐标系(如图)
为x轴正向建立空间直角坐标系(如图)
![]() 则题意得:O(0,0,0),A(2
则题意得:O(0,0,0),A(2![]() ,2,0)
,2,0)
 B(0,4,0),C(0,0,2)
B(0,4,0),C(0,0,2)
D(![]() ,1,0),E(
,1,0),E(![]() ,3,0)
,3,0)
![]()
![]() 取平面CDE的法向量
取平面CDE的法向量![]() =(2,0,
=(2,0,![]() )
)
取平面OAB的法向量![]() =(0,0,2)
cos<
=(0,0,2)
cos<![]() ,
,![]() >=
>=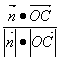 =
=![]() =
=![]()
∴二面角O—DE—C的大小为arccos![]()
20. (I)![]() ;
;
(Ⅱ)![]() ;
;
(Ⅲ)![]() .
.
21.(Ⅰ)由![]() …①,
…①,![]() ,∴
,∴![]() …②.
…②.
由中点坐标公式![]() .
.
(Ⅱ)又![]() 在双曲线上,∴
在双曲线上,∴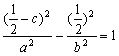 …③.
…③.
联立①②③,解得![]() ,
,![]() .
.
∴双曲线方程为![]() .
.
注:对点M用第二定义,得![]() ,可简化计算.
,可简化计算.
(Ⅲ)由(Ⅱ),![]() ,设
,设![]() ,
,![]() ,m:
,m:![]() ,
,
则由![]() ,得
,得![]() ,
,![]() .
.
由![]() ,得
,得![]() .
.
∴![]() ,
,![]() .
.![]() .
.
由![]() ,
,![]() ,
,![]() ,消去
,消去![]() ,
,![]() ,
,
得![]() .
.
∵![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() .
.
又直线m与双曲线的两支相交,即方程![]() 两根同号,
两根同号,
∴![]() . ∴
. ∴![]() ,故
,故![]() .
.
22.解:(I)∵![]() ,∴
,∴![]() .
.
∴![]() . ∴
. ∴![]() .
.
下面用数学归纳法证明:![]() .
.
①![]() 时,
时,![]() ,故结论成立.
,故结论成立.
②假设![]() 时结论成立,即
时结论成立,即![]() .
.
∴![]() ,即
,即![]() .
.
也就是说![]() 时,结论也成立.
时,结论也成立.
由①②可知,对一切![]() 均有
均有![]() .
.
(Ⅱ)要证![]() ,
,
即证![]() ,其中
,其中![]() .
.
令![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
|
|
|
|
|
|
| + | 0 | — |
|
|
| 极大值 |
|
又![]() ,
, ![]() .
.
∴当![]() ,
,![]() . ∴
. ∴![]() .
.
∴![]() . 即
. 即![]() .
.
(Ⅲ)由(Ⅱ)知:![]() .
.
∴ .
.
∴![]() .
.
又![]() ,即
,即![]() . ∴
. ∴![]() .
.