08届高中毕业班文科数学第一次模拟考试

08届高中毕业班文科数学第一次模拟考试

数学试题（文科）

1.设集合M＝｛x｜x≤m｝，N＝｛y｜y＝2^－x，x∈R｝，若M∩N≠，则实数m的取值范围是

　　　A.m≥0　　　　B.m＞0　　　 C.m≤0　　　　　　 D.m＜0

2. 在复平面内，复数对应的点位于

(A)第一象限 （B）　第二象限 （C）　第三象限　（D）　第四象限

3. 某射手的一次射击中，射中10环、9环、8环的概率分别为0.2、0.3、0.1，则此射手在一次射击中不超过8环的概率为

　　　A.0.5　　　　　　　 B.0.3　　　　　　　 C.0.6　　　　　　　 D.0.9

4、如图是年元旦晚会举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和样本方差分别为

A．，2　 B．，3

C．，2　 D．，3

5.设是一次函数，若，且成等比数列，则等于　　　　　　　　　　　　　　 

A　　B　 　　C　　　D　

6. 若，则角的终边一定落在直线（　　）上

（A） 　（B）  （C）　 （D）

7、已知向量与的夹角为，且则等于　　　　　

A　 5　　　　　　  B　 4　　　　　　　　　 C　3　　　　　　　　 D　 1

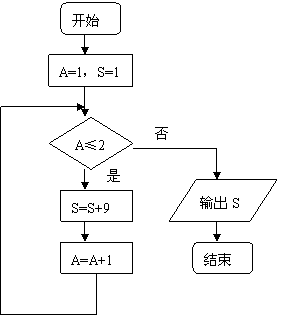8 如图，该程序运行后输出的结果为　

　　A．1　　　B．10　　　 C ．19　　　　D．28

9.设α、β表示平面，为直线，不在平面α，β内，有下列三个事实，以任意两个作为条件，另一个作为结论可构造三个命题，其中正确命题的个数是　　　　　　　　

　　　①　　　②　　 ③

　　　A.1　　　　　　B.2　　　　　　C.3　　　　　　D.0

10已知双曲线的焦点为、，点在双曲线上且轴，则到直线的距离为

　 A.　　B.　　  C.　　　　D.

11.设函数y＝f(x)在定义域内可导，y＝f(x)的图象

如图所示，则导函数y＝f′(x)的大致图象为　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　 A.　　　　　　　　　　　　 B.　　　　　　　　　　　　 C.　　　　　　　　　　　　 D.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

12、对任意整数，函数满足，若，那么等于　　　　　　　　　　　　　　　　　　　　　　　　　　　 

A　 －1　　　　　　  B　 1　　　　　  C　 19　　　　　　 D　 43

13.条件p：｜x｜＞1　条件q：x＜－2，则“p是q的 　条件”（填写“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要“）

 14、奇函数在上是增函数，在区间上的最大值为8，最小值为－1，则　　

15.在平面直角坐标系中，不等式组，表示的平面区域的面积是_______

16　已知下列命题：①；②函数的图像向左平移1个单位后得到的函数图像解析式为；③函数的图像与函数的图像关于对称; ④满足条件的三角形△ABC有两个.

 其中正确命题的序号是　　　　　　 .

17. 已知△ABC中，A、B、C所对的边分别为a、b、c，当a²＞b²+c²

且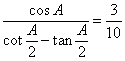时，求sin2A的值.

18 已知函数

　 （1）若f（x）在上增函数，求实数a的取值范围；

　 （2）若x=3是f（x）的极值点，求f（x）在上的最小值和最大值.

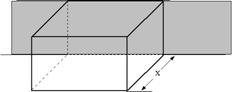
19.一个多面体的直观图及三视图如图所示（其中M、N分别是AF、BC的中点）

　　　

①求证：MN∥平面CDEF.

②求多面体A—CDEF的体积.

20 某单位建造一间地面面积为12m²的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x不得超过a米，房屋正面的造价为400元/m²，房屋侧面的造价为150元/m²，屋顶和地面的造价费用合计为5800元，如果墙高为3m，且不计房屋背面的费用.

　 （1）把房屋总价y表示成x的函数，并写出该函数的定义域.

　 （2）当侧面的长度为多少时，总造价最底？最低总造价是多少？

21. 已知数列{a_n}满足

　 （1）求数列的前三项：a₁，a₂，a₃；

　 （2）是否存在一个实数λ，使得数列为等差数列？若存在，求出λ的值；若不存在，说明理由；

（3）求数列{a_n}的前n项和S_n.

22椭圆的中心在原点O，短轴长为，左焦点为，直线与轴交于点A，且，过点A的直线与椭圆相交于P，Q两点.

（1）求椭圆的方程.

（2）若，求直线PQ的方程.

BDACA  DBDCC　DC

充分不必要　 －15　　4　　 ③

17.

解：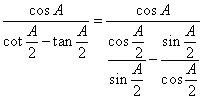

＝

………………6分

　　　a²＞b²+c²

………………10分

………………12分

18.解：（I）上是增函数，则有

　　

　　 又（当且仅当x=1时取等号），所以a≤3………6分

　 （II）由题意知=3x²－2ax+3=0的一个根为x=3，可得a=5，

　　所以=3x²－10x+3=0的根为x=3或x=（舍去），又f(1)=－1，

　　f(3)=－9,f(5)=15，

∴f(x)在x∈[1，5]上的最小值是f(3)=－9，最大值是f(5)=15……12分

19.由三视图知，该多面体是底面为直角三角形的直三棱柱ADE—BCF，且AB＝BC＝BF＝2，DE＝CF＝，∠CBF＝

①证明：取BF的中点G，连结MG、NG，由M、N分别为AF、BC中点，可得，NG∥CF，MG∥EF

　　　　　　  ……6分

②取DE中点为H，因为AD＝AE

DE

在直三棱柱AED—BCF中

平面ADE⊥平面CDEF

面ADE∩面CDEF＝DE

多面体A—CDEF是以AH为高，以矩形CDEF为底面的棱锥

在△ADE中，AH＝

S_矩形CDEF＝DE·EF＝4

……12分

20.解：（1）由题意可得，

………………5分

（2）

当且仅当时取等号……………………7分

若时，有最小值13000.………………8分

若，任取

　　



上是减函数………………10分

有最小值………………12分

（此题利用导数相应得分）

21.解：（1）由

　　同理可得　　a₂ = 13， a₁ = 5.　　　　　　　　　　　　　　　  3分

　 （2）假设存在的实数λ符合题意，则

　　　　

　　　　必是与n无关的常数，则

　　　 　　　　　　　　　　　　　　　　　 7分

　　故存在实数λ=－1，使得数列为等差数列.

　（3）由（2）知数列是公差d = 1的等差数列

　　　　9分

　　S_n = n+2×2 + 3×2² + 4×2³ +…+(n+1)·2ⁿ⁺¹

　　2S_n = 2n+2×2² + 3×2² +…+n·2ⁿ + (n+1)·2ⁿ⁺¹

　　　 相减整理得：　S_n = n（2ⁿ⁺¹ +1）　　　　　　　　　　  12分

22解：（1）设，则，，

解得＝4，c＝1，所以椭圆方程为。……………4分

（2）设PQ的方程为

因为PF⊥QF，所以，

即，

……………8分

联立得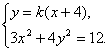

消去y，得，……………10分

由，得……………11分

所以.……………12分

代入（*）式化简，得8k²＝1，所以

则直线PQ的方程为.……………14分