绝密★启用前
08高考理科数学第二次月考模拟试题
理科数学
命题人:杨正宏 张兴虎 杨发勇 期望值:80分
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅱ卷第22题为选考题,其他题为必考题。考生做答时,将答案答在答题卡上,在本试卷上答题无效。考试结束后,将本试卷和答题卡一并交回。
注意事项:
1、答题前,考生先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的准考证号、姓名,并将条形码粘贴在指定位置上。
2、选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或炭素笔书写,字体工整、笔迹清楚。
3、请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4、保持卡面清洁,不折叠,不破损。
5、作选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的标号涂黑。
参考公式:
样本数据![]() ,
,![]() ,
,![]() ,
,![]() 的标准差 锥体体积公式
的标准差 锥体体积公式
![]()
![]()
其中![]() 为标本平均数 其中
为标本平均数 其中![]() 为底面面积,
为底面面积,![]() 为高
为高
柱体体积公式 球的表面积、体积公式
![]()
![]() ,
,![]()
其中![]() 为底面面积,
为底面面积,![]() 为高 其中
为高 其中![]() 为球的半径
为球的半径
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合A={x1![]() x
x![]() 2},B={xx
2},B={xx![]() a}.若A
a}.若A![]() B则a的范围是
B则a的范围是
(A) a<1 (B) a![]()
![]() 2
2
(2)在复平面内,复数![]() 对应的点所在的象限是
对应的点所在的象限是
(A)一 (B) 二 (C) 三 (D) 四
(3)函数![]() 的 图像的两条相邻对称轴间的距离为
的 图像的两条相邻对称轴间的距离为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(4)已知双曲线![]() 垂直,则a的值是
垂直,则a的值是
(A) ![]() (B) 2 (C) 4 (D) 16
(B) 2 (C) 4 (D) 16
(5)阅读右边程序,其运算结果是
 (A) 20 (B) 24 (C) 45 (D) 56
(A) 20 (B) 24 (C) 45 (D) 56
(6)函数![]() 的零点所在的大致区间是
的零点所在的大致区间是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(7)若![]() 是互不重合的直线,
是互不重合的直线,![]() 是不重合的平面,则下列命题中为真命题的是
是不重合的平面,则下列命题中为真命题的是
(A)若![]() ,
,![]() ,
,![]() ,则
,则![]()
(B)若![]() ,
,![]() ,则
,则![]()
(C)若![]() ,
,![]() ,则
,则![]()
![]() ∥
∥ ![]()
(D)若![]() ,
,![]()
![]() ∥
∥![]() ,则
,则![]()
(8)在![]() 的展开式中,含
的展开式中,含![]() 的项的系数是以
的项的系数是以![]() 为通项的数列
为通项的数列![]() 的第( )项
的第( )项
(A)24 (B) 12 (C) 11 (D) 10
 (9)如果一个几何体的三视图如右图所示,
(9)如果一个几何体的三视图如右图所示,
则此几何体的表面积为( )
(A)![]() (B)
(B)![]()
(C) 96 (D) 80
(10)锐角三角形ABC中,若![]() ,则
,则![]() 的范围是
的范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)函数![]() 内的交点为P,它们在点P处的两条切线与x轴所围成的三角形的面积为
内的交点为P,它们在点P处的两条切线与x轴所围成的三角形的面积为
(A) ![]() (B)
(B) ![]() (C) 2
(C) 2![]() (D) 4
(D) 4![]()
(12)以下四个命题:
①![]()
②定义![]()
③等比数列![]() .
.
④把函数![]() 的图像向右平移2个单位后得到的图像对应的解析式为
的图像向右平移2个单位后得到的图像对应的解析式为![]() .
.
其中正确命题的是
(A) ①② (B) ②④ (C) ③④ (D) ①④
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题--第21题为必考题,每个试题考生都必须做答。第22题为选考题,考生根据要求做答。
二、填空题:本大题共小题,每小题5分.
(13)若命题“![]() x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
(14)在区间[1, 5 ]上分别取一个实数,记为m ,则方程![]() 表示焦点在x轴上的椭圆的概率是____________________
表示焦点在x轴上的椭圆的概率是____________________
(15)若三角形内切圆半径为![]() ,三边长分别为
,三边长分别为![]() ,则三角形的面积
,则三角形的面积![]() ,根据类比思想,若四面体内切球半径为
,根据类比思想,若四面体内切球半径为![]() ,其四个面的面积分别为
,其四个面的面积分别为![]() ,则四面体的体积
,则四面体的体积![]() ________
________
(16)某小卖部为了了解热茶销售量y(杯)与气温x(![]() )之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
| 气温x( | 18 | 13 | 10 | -1 |
| 杯数y | 24 | 34 | 38 | 64 |
由表中数据算得线性回归方程![]() 中的
中的![]() ,预测当气温为
,预测当气温为![]() 时,热茶销售量为____杯.(回归系数
时,热茶销售量为____杯.(回归系数 )
)
三、解答题: 解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分12分)
已知平面内三点A(3,0),B(0,3),C(![]() ,O为坐标原点.
,O为坐标原点.
(1) 若![]()
(2) 若![]() 的夹角。
的夹角。
(18)(本小题满分12分)
盒子中装着有标数字1,2,3,4,5的上卡片各2张,从盒子中任取3张卡片,每张卡片被取出的可能性都相等,用![]() 表示取出的3张卡片上的最大数字,求:
表示取出的3张卡片上的最大数字,求:
(1)取出的3张卡片上的数字互不相同的概率;
(2)随机变量![]() 的概率分布和数学期望;
的概率分布和数学期望;
(19)(本小题满分12分)
 如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF
如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF![]() 平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
(1)求证:![]()
(2)若FG=GD,求证:GA//平面FMC.
(3)若DF=DA,求二面角F-MC-D的正弦值
(20)(本小题满分12分)
设椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 、
、![]() ,
,![]() 是椭圆
是椭圆![]() 上的一点,且
上的一点,且![]() ,坐标原点
,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上的一点,过点
上的一点,过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
(21)(本小题满分12分)
已知函数![]()
(I)若![]() 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数![]() 的最小值;
的最小值;
(III)设函数![]() 的图象C1与函数
的图象C1与函数![]() 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
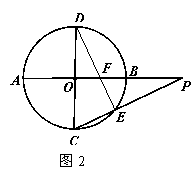 (22) 请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分。作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑。
(22) 请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分。作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑。
(22) A (本小题满分10分)选修4-1:几何证明选讲
如图2所示,![]() 与
与![]() 是⊙O的直径,
是⊙O的直径,![]()
![]()
![]() ,
,![]() 是
是![]() 延长线上一点,连
延长线上一点,连![]() 交⊙O于点
交⊙O于点![]() ,连
,连![]() 交
交![]() 于点
于点![]() ,若
,若![]() .
.
求证:![]()
(22) B (本小题满分10分)选修4-4:坐标系与参数方程
在曲线![]() :
:![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
: 的距离最小,并求出该点坐标和最小距离。
的距离最小,并求出该点坐标和最小距离。
.
(22) C (本小题满分10分)选修4-5:不等式选讲
若![]() 三点共线,求
三点共线,求![]() 的最小值。
的最小值。
08高考理科数学第二次月考模拟试题
考试数学(理)试卷答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | B | B | D | B | D | D | A | C | B | D |
二、填空题
(13)[-1,3] (14)![]() (15)
(15)![]() (16)70
(16)70
(17)解:(1)![]() ……………………1分
……………………1分
![]() ……………………3分
……………………3分
得![]() ……………………4分
……………………4分
![]() ……………………5分
……………………5分
![]() …………………………………………6分
…………………………………………6分
(2)![]()
![]() ……………………8分
……………………8分
![]() ……………………9分
……………………9分
![]()
![]() ……………10分
……………10分
则 ……………………11分
……………………11分
![]() 即为所求。……………………12分
即为所求。……………………12分
18. (1)记"一次取出的3张卡片上的数字互不相同的事件"为A,
则![]()
(2)由题意![]() 有可能的取值为:2,3,4,5
有可能的取值为:2,3,4,5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以随机变量![]() 的概率分布为:
的概率分布为:
| | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
所以![]() 的数学期望为E
的数学期望为E![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]()
19.证明:由已知可得为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC
(1)连接DB,可知B、N、D共线,且AC⊥DN
又FD⊥AD FD⊥CD,
![]() FD⊥面ABCD
FD⊥面ABCD
![]() FD⊥AC
FD⊥AC
![]() AC⊥面FDN
AC⊥面FDN ![]()
![]() GN⊥AC…………………………………………4分
GN⊥AC…………………………………………4分
(2)证明:取DC中点S,连接AS、GS、GA
![]() G是DF的中点,
G是DF的中点,![]() GS//FC,AS//CM
GS//FC,AS//CM
![]() 面GSA//面FMC
面GSA//面FMC
![]()
![]() GA//面FMC 即GP//面FMC………………8分
GA//面FMC 即GP//面FMC………………8分
(3)设DF=DA=2,则各点的坐标为
C(0,2,0) F(0,0,2) M(2,1,0)
![]() = (2,1,-2)
= (2,1,-2) ![]() =(-2,1,0)
=(-2,1,0)
设平面FMC的法向量为n1=(x,y,1),
则![]() · n1=0
· n1=0 ![]() ·n1=0
·n1=0
即:![]()
解得:![]()
n1=(![]()
又平面AMC的法向量为n2=(0,0,1)
cos< n1 ,n2>=![]() =
=![]()
二面角F-MC-D的正弦值为![]() ……………………12分
……………………12分
20(Ⅰ)由题设知![]()
由于![]() ,则有
,则有![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]()
故![]() 所在直线方程为
所在直线方程为![]() …………2分
…………2分
所以坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]()
又![]() ,所以
,所以![]()
解得:![]()
所求椭圆的方程为![]() …………5分
…………5分
(Ⅱ)由题意可知直线![]() 的斜率存在,设直线斜率为
的斜率存在,设直线斜率为![]()
直线![]() 的方程为
的方程为![]() ,则有
,则有![]() …………7分
…………7分
设![]() ,由于
,由于![]() 、
、![]() 、
、![]() 三点共线,且
三点共线,且![]()
根据题意得![]()
解得 或
或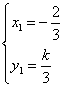 …………10分
…………10分
又![]() 在椭圆
在椭圆![]() 上,故
上,故![]() 或
或
解得![]()
综上,直线![]() 的斜率为
的斜率为![]() 或
或![]() .…………12分
.…………12分
21.解:(I)依题意:![]()
![]() 在(0,+
在(0,+![]() )上是增函数,
)上是增函数,
![]() 对x∈(0,+
对x∈(0,+![]() )恒成立, …………2分
)恒成立, …………2分

![]() …………4分
…………4分
(II)设![]()

当t=1时,ym I n=b+1; …………6分

当t=2时,ym I n=4+2b …………8分

当![]() 的最小值为
的最小值为![]() …………8分
…………8分
(III)设点P、Q的坐标是![]()
则点M、N的横坐标为![]()
C1在点M处的切线斜率为![]()
C2在点N处的切线斜率为![]()
假设C1在点M处的切线与C2在点N处的切线平行,则![]()

……………10分
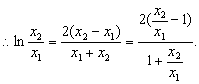
设![]() ……………… ①
……………… ①

这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行. …………12分
22.选做题
A.  证明:
证明:![]()
![]()
![]()
![]()
![]() ∽
∽![]()
![]()
![]()
![]()
![]()
B.直线C2化成普通方程是x+y-2![]() -1=0……………………………………2分
-1=0……………………………………2分
设所求的点为P(1+cos![]() ,sin
,sin![]() ),……………………………………………3分
),……………………………………………3分
则C到直线C2的距离d=![]() …………………………5分
…………………………5分
=sin(![]() +
+![]() )+2……………………………………7分
)+2……………………………………7分
当![]() 时,即
时,即![]() =
=![]() 时,d取最小值1………………………………9分
时,d取最小值1………………………………9分
此时,点P的坐标是(1-![]() ,-
,-![]() )……………………………………10分
)……………………………………10分
C.解:根据题意,![]() …………………………2分
…………………………2分
![]()
![]()
![]() ,……………………………5分
,……………………………5分
![]() 。………………8分
。………………8分
![]() 当且仅当
当且仅当![]() 时等号成立,
时等号成立,
![]() ……………………………………10分
……………………………………10分