高考理科数学第二轮复习综合测试
本试卷分为第I卷（选择题）和第II卷（非选择题）两部分.满分150分.考试时间120分钟.
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．定义差集A-B={xx∈A,且x
B},现有三个集合A、B、C分别用圆表示，则集合C-(A-B)可表示下列图中阴影部分的为 （ ）
|
2．复数
的共轭复数是 （ ）
A．
B．
C．
D．
3．已知
是两条不重合的直线，
是三个两两不重合的平面，给出下列命题：
①若
∥
，
∥且
则
∥；
②若
∥，则∥且∥；
③若
∥则
；
④若∥，且
则∥．
其中的正确的命题是 （ ）
A．①② B．③④ C．①③ D．②④
4．圆心在抛物线
上的动圆过点（0,1），且与定直线
相切，则直线的方程为（ ）
A．
B． 
C．
D． 
5．若
，且
，则 （ ）
A．
B．
C．
D．
6．设函数
，则对于任意的实数
和
，
是
的 （ ）
A．必要不充分条件 B．充分不必要条件
C．充分且必要条件 D．既不充分又不必要条件
7．若函数
（为常数），在
内为增函数，则实数的取值范围是（ ）
A．
B．
C．
D．
8．已知点
是椭圆C：
上的动点，
分别为左、右焦点，O是坐标原点，则
的取值范围为 （ ）
A．
B．
C．
D．
9．已知棱长为的正四面体ABCD有内切球O，经过该棱锥A—BCD的中截面为M，则O到平面M的距离为 （ ）
A．
B．
C．
D．
10．在平面直角坐标系中，x轴的正半轴上有4个点，y轴的正半轴上有5个点，这9个点任意两点连线，则所有连线段的交点落入第一象限的个数最多是 （ ）
A．30 B．60 C．120 D．240
11．在算式“4×□+1×△=30”的两个□、△中，分别填入两个正整数，使它们的倒数之和最小，则这两个数构成的数对（□, △）应为 （ ）
A．（4, 14） B．（6, 6） C．（3, 18） D．（5, 10）
12．某种电热器的水箱盛水200升，加热到一定温度可浴用．浴用时，已知每分钟放水34升，在放水的同时按匀加速度自动注水（即t分钟自动注水2t2升），当水箱内的水量达到最小值时，放水自动停止．现假定每人洗浴用水量为65升，则该电热器一次至多可供 （ ）
A．3人洗浴 B．4人洗浴 C．5人洗浴 D．6人洗浴
第Ⅱ卷（非选择题 共90分）
|
13．如右图是由三个相同的正方形相接，在
中，
锐角
，则
_______.
14．若
，且
，则
15．有４个不等式：
．
其中不正确的个数是___ ___.
16．若连续且不恒等于的零的函数
满足
，试写出一个符合题意的函数
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）已知函数
的图像关于原点
对称，试求函数的解析式．
18．（本小题满分12分）某次有奖竞猜活动中，主持人准备了A、B两个相互独立的问题， 并且宣布：观众答对问题A可获奖金a元，答对问题B可获奖金2a元；先答哪个题由观众自由选择；只有第1个问题答对，才能再答第2个问题，否则中止答题。若你被选为幸运观众，且假设你答对问题A、B的概率分别为
、
.你觉得应先回答哪个问题才能使你获得奖金的期望较大？说明理由.
19．（本小题满分12分）
在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PA垂直于底面，E、F分别是AB、PC的中点.
（I）求证：
平面PAD；
（II）当平面PCD与平面ABCD成多大二面角时，
直线
平面PCD？
20．（本小题满分12分）已知函数
在（1，2
是增函数，
在（0，1）为减函数.
（Ⅰ）求、
的表达式；
（Ⅱ）求证：当
时，方程
有唯一解.
|
为x轴，AC的中垂线为y轴建立直角坐标系xoy.
（Ⅰ）证明存在两个定点E、F，使得BE+BF为定长；
并求出点E、F的坐标及点B的轨迹Γ；
（Ⅱ）设P为轨迹Γ上的任一点，点M、N分别在射线
PA、PC上，动点Q满足
，
经过点A且以
为方向向量的直线与动
点Q的轨迹交于点R，试问：是否存在一个定点D，
使得
为定值？若存在，求出点D的坐标；若不存在，说明理由？
22．在f（m，n）中，m、n、f（m，n）均为非负整数，且对任何m，n有：
（Ⅰ）
；
（Ⅱ）
；
（Ⅲ）
试求：（I）f（1，0）的值；
（II）f（1，n）关于n的表达式；
（III）f（3，n）关于n的表达式.
参考答案
一、选择题
1．A．观察选择支A，我们就不难发现，它正好表示集合C-(A-B)．
2．B．因为
，所以
．
3．B．用特殊办法检验知道，①不成立排除A和C，检验知③成立．
4．D．抛物线的焦点为
，由抛物线的定义，我们知道，定直线是抛物线的准线，于是有．
5．B．
，
，
，故应该选B．
6．C．显然，函数
在
上是递增函数，而且是奇函数，于是，由
，得
，有
，即
．反过来，也成立．
7．A．因为
，所以由题意，可得
在上恒成立，即
．当
时，
恒成立，所以当时，函数不是单调递增函数，所以
．
8．D．设椭圆与
轴的交点为
，与
轴的交点为
．考虑2个极端状态：
当点P在A点时，有
，所以
；
当点P在B点时，有
，
，
，
所以
．故有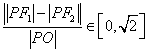
.
9．C．设内切球的半径为
，运用等体积法，有
所以
于是，中截面
到底面的距离为
，则
到平面的距离为
．
10．B．构造凸四边形，凸四边形对角线的交点在凸四边形内．最多其有
=60.
11．D．设
□，
△，则
．
取等号时，有
，即
12．B．设t分钟后水箱内的水量为升，则由题设知，
，
当
时，取最小值，此时共放浴用水
升，而
，故一次至多可供4人洗浴．
二、填空题
13．
．记右下角的顶点为D，显然有 
，于是
．
14．
．若
或
，则一定有
，从而有
．若
且
，
对取以６为底的对数，得
，
于是
故有
综合以上知道 
．
15．０．这４个不等式都是正确的．如：
．
16．
A是非零的常数．注意到
于是可想到
．
三、解答题
17．变形，得
． （3分）
因为函数的图像关于原点对称，
所以
． （5分）
也就是等式
对于任意
都成立．
于是有 
，
即 
， （8分）
对于任意都成立，从而只能有
．解得
故所求函数的解析式为
或
． （１２分）
18．设甲先答A、B所获奖金分别为
元，则有
（5分）
（8分）
|
． （10分）
由于两种答序获奖金的期望相等，故先答哪个都一样． （12分）
19．（I）取CD中点G，连结EG、FG．
∵E、F分别是AB、PC的中点，
∴EG//AD，FG//PD， （4分）
∴平面EFG//平面PAD，
∴ EF//平面PAD． （5分）
（II）当平面PCD与平面ABCD成45°角时，直线EF^平面PCD.
∵G为CD中点，则EG^CD．
∵PA^底面ABCD，∴AD是PD在平面ABCD内的射影．
∵CDÌ平面ABCD，且CD^AD，
故CD^PD． （8分）
又∵FG∥PD，
∴FG^CD，
故ÐEGF为平面PCD 与平面ABCD所成二面角的平面角，即ÐEGF=45°．（10分）
从而得ÐADP=45°， AD=AP.由，得PE=CE.又F是PC的中点，
∴EF^PC.
由CD^EG，CD^FG，得CD^平面EFG，∴CD^EF，即EF^CD，
故EF^平面PCD． （12分）
20．（Ⅰ）
依题意
又∵
，依题意
（3分）
（6分）
（II）由（I）可知，原方程为
设
令
令
（9分）
由
|
| （0，1） | 1 | （1，+∞） |
|
| － | 0 | + |
|
| 递减 | 0 | 递增 |
即
在
处有一个最小值0，即当
时，>0，
只有一个解.
即当x>0时，方程有唯一解.（12分）
21．（I）由sinA、sinB、sinC构成公差为正的等差数列，得a+c=2b，且a>b>c．
因a+b+c=12，故a+c=8，即BC+BA=8为定值．（3分）
注意到 8>AC=4，且BC>BA，
故B的轨迹是以A、C为焦点，8为长轴长，在y轴左侧且除去顶点的椭圆的一部分．并且存在定点E、F，它们分别为A、C，从而它们的坐标分别为（-2，0），（2，0）．（6分）
|
，则以PMN为
顶点可作出一个菱形PMTN，于是
，
，
且
，从而PQ为∠APC的外角∠SPA的平分线．
过A且以为方向向量的直线
AS⊥PQ．
从而
， （10分）
于是只须取AC的中点为D（O），
即有=4为定值．故存在定点D，而为定值． （12分）
22．
． （2分）
，
，
，
，
，
，
． （5分）
．
，
．
．
， （7分）
，
．，
． （9分）
．
． （14分）