高考数学三角函数解答题选编
1.（2006安徽卷）已知
（Ⅰ）求
的值；
（Ⅱ）求
的值.
2.（2006北京卷）已知函数
，
（Ⅰ）求
的定义域；
（Ⅱ）设
是第四象限的角，且
，求
的值.
3.（2006福建卷）已知函数f(x)=sin2x+
sinxcosx+2cos2x,x
R.
（I）求函数f(x)的最小正周期和单调增区间；
（Ⅱ）函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到？
4.（2006广东卷）已知函数
.
(I)求
的最小正周期；
(II)求的的最大值和最小值；
(III)若
，求
的值.
5.（2006湖南卷）已知
求θ的值.
6.（2006辽宁卷）已知函数
，
.求:
(I)
函数的最大值及取得最大值的自变量
的集合；
(II)
函数的单调增区间.
7.(2006陕西卷)已知函数f(x)=sin(2x－)+2sin2(x－) (x∈R)
(Ⅰ)求函数f(x)的最小正周期；
(II)求使函数f(x)取得最大值的x的集合.
8.(2006上海卷)求函数
＝2
＋
的值域和最小正周期．
9.(2006上海卷)已知
是第一象限的角，且
，求
的值.
10.（2006天津卷）已知
，
．求
和
的值．
11.（2007安徽理）已知
为
的最小正周期，
，且
．求
的值．
12.（2007广东理）已知
顶点的直角坐标分别为
，
，
．
（1）若
，求
的值；
（2）若
是钝角，求
的取值范围．
13.（2007湖北文）已知函数
，
．
（I）求的最大值和最小值；
（II）若不等式
在上恒成立，求实数
的取值范围．
14.（2007湖南文）已知函数
．求：
（I）函数的最小正周期；
（II）函数的单调增区间．
15.（2007全国卷1理）设锐角三角形
的内角
的对边分别为
，
．
（Ⅰ）求
的大小；
（Ⅱ）求
的取值范围．
16.（2007山东文）在中，角的对边分别为
．
（1）求
；
（2）若
，且
，求．
17.（2007陕西理）设函数
，其中向量
，
，
，且
的图象经过点
．
（Ⅰ）求实数
的值；
（Ⅱ）求函数
的最小值及此时值的集合．
18.（2007四川理）已知
<
<
<
,
(Ⅰ)求
的值.
（Ⅱ）求.
19.（2007天津文）在中，已知
，
，
．
（Ⅰ）求
的值；
（Ⅱ）求
的值．
20.（2007浙江理）已知的周长为
，且
．
（I）求边
的长；
（II）若的面积为
，求角
的度数．
06、07年高考三角函数解答题选编
1.（2006安徽卷）已知
（Ⅰ）求的值；
（Ⅱ）求的值。
解：(Ⅰ)由，得
，所以＝
。
（Ⅱ）∵
，∴
。
2.（2006北京卷）已知函数，
（Ⅰ）求的定义域；
（Ⅱ）设是第四象限的角，且，求的值.
解：（1）依题意，有cosx¹0，解得x¹kp＋
，
即的定义域为｛xxÎR，且x¹kp＋，kÎZ｝
（2）＝－2sinx＋2cosx\＝－2sina＋2cosa
由是第四象限的角，且可得sina＝－
，cosa＝
\＝－2sina＋2cosa＝
3.（2006福建卷）已知函数f(x)=sin2x+xcosx+2cos2x,xR.
（I）求函数f(x)的最小正周期和单调增区间；
（Ⅱ）函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到？
本小题主要考查三角函数的基本公式、三角恒等变换、三角函数的图象和性质等基本知识，以及推理和运算能力。满分12分。
解：（I）
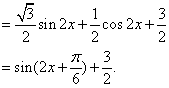
的最小正周期
由题意得
即 
的单调增区间为
（II）方法一： 先把
图象上所有点向左平移
个单位长度，得到
的图象，再把所得图象上所有的点向上平移
个单位长度，就得到
的图象。
方法二：把图象上所有的点按向量
平移，就得到的图象。
4.（2006广东卷）已知函数.
(I)求的最小正周期；
(II)求的的最大值和最小值；
(III)若，求的值.
解：
（Ⅰ）的最小正周期为
;
（Ⅱ）的最大值为
和最小值
；
（Ⅲ）因为
，即
,即 
5.（2006湖南卷）已知
求θ的值.
解析： 由已知条件得
.
即
.
解得
.
由0＜θ＜π知
，从而
.
6.（2006辽宁卷）已知函数，.求:
(I) 函数的最大值及取得最大值的自变量的集合；
(II) 函数的单调增区间.
【解析】(I) 解法一:
当
,即
时, 取得最大值
.
函数的取得最大值的自变量的集合为
.
解法二:
当,即时, 取得最大值.
函数的取得最大值的自变量的集合为.
(II)解: 
由题意得: 
即: 
因此函数的单调增区间为
.
【点评】本小题考查三角公式,三角函数的性质及已知三角函数值求角等基础知识,考查综合运用三角有关知识的能力.
7.(2006陕西卷)已知函数f(x)=sin(2x－)+2sin2(x－) (x∈R)
(Ⅰ)求函数f(x)的最小正周期 ; (2)求使函数f(x)取得最大值的x的集合.
解:(Ⅰ) f(x)=sin(2x－)+1－cos2(x－)
= 2[sin2(x－)－ cos2(x－)]+1
=2sin[2(x－)－]+1
= 2sin(2x－) +1
∴ T==π
(Ⅱ)当f(x)取最大值时， sin(2x－)=1，有 2x－ =2kπ+
即x=kπ+ (k∈Z) ∴所求x的集合为{x∈Rx= kπ+ ， (k∈Z)}．
8.(2006上海卷)求函数＝2＋的值域和最小正周期．
[解] 
∴ 函数的值域是
,最小正周期是
；
9.(2006上海卷)已知是第一象限的角，且，求的值。
解：
=
由已知可得sin
,
∴原式=
.
10. （2006天津卷）已知
，．求和的值．
本小题考查同角三角函数关系、两角和公式、倍角公式等基础知识，考查基本运算能力。
解法一：由
得
则
因为
所以
解法二：由得 
解得
或
由已知故舍去
得 
因此，
那么 
且
故
11.（2007安徽理16）已知为的最小正周期， ，且．求的值．
本小题主要考查周期函数、平面向量数量积与三角函数基本关系式，考查运算能力和推理能力．本小题满分12分．
解：因为
为
的最小正周期，故
．
因
，又
．
故
．
由于
，所以
12.（2007广东理16）已知顶点的直角坐标分别为，，．
（1）若，求的值；
（2）若是钝角，求的取值范围．
解析： （1）
，
，若c=5， 则
，∴
，∴sin∠A＝
；
2）若∠A为钝角，则
解得
，∴c的取值范围是
；
13.（2007湖北文16）已知函数，．
（I）求的最大值和最小值；
（II）若不等式在上恒成立，求实数的取值范围．
本小题主要考查三角函数和不等式的基本知识，以及运用三角公式、三角函数的图象和性质解题的能力．
解：（Ⅰ）
．
又
，
，即
，
．
（Ⅱ）
，，
且
，
，即的取值范围是
．
14.（2007湖南文16）
已知函数．求：
（I）函数的最小正周期；
（II）函数的单调增区间．
解：
．
（I）函数的最小正周期是
；
（II）当
，即
（
）时，函数
是增函数，故函数的单调递增区间是
（）．
15.（2007全国卷1理17）
设锐角三角形的内角的对边分别为，．
（Ⅰ）求的大小；
（Ⅱ）求的取值范围．
解：（Ⅰ）由，根据正弦定理得
，所以
，
由为锐角三角形得
．
（Ⅱ）
．
由为锐角三角形知，
，
．
，
所以
．
由此有
，
所以，的取值范围为
．
16.（2007山东文17）
在中，角的对边分别为．
（1）求；
（2）若，且，求．
解：（1）
又
解得
．
，
是锐角．
．
（2）
，
，
．
又
．
．
．
．
17.（2007陕西理17）设函数，其中向量，，，且的图象经过点．
（Ⅰ）求实数的值；
（Ⅱ）求函数的最小值及此时值的集合．
解：（Ⅰ）
，
由已知
，得
．
（Ⅱ）由（Ⅰ）得
，
当
时，的最小值为
，
由，得值的集合为
．
18.（2007四川理17）
已知<<<,
(Ⅰ)求的值.
（Ⅱ）求.
本题考察三角恒等变形的主要基本公式、三角函数值的符号，已知三角函数值求角以及计算能力。
解：（Ⅰ）由
，得
∴
，于是
（Ⅱ）由
，得
又∵
，∴
由
得：
所以
19.（2007天津文17）
在中，已知，，．
（Ⅰ）求的值；
（Ⅱ）求的值．
本小题考查同角三角函数的基本关系式、两角和公式、倍角公式、正弦定理等的知识，考查基本运算能力．满分12分．
（Ⅰ）解：在中，
，由正弦定理，
．
所以
．
（Ⅱ）解：因为，所以角
为钝角，从而角为锐角，于是
，
，
．
．
20.（2007浙江理18）
已知的周长为，且．
（I）求边的长；
（II）若的面积为，求角的度数．
解：（I）由题意及正弦定理，得
，
，
两式相减，得
．
（II）由的面积
，得
，
由余弦定理，得
，
所以
．