08乌鲁木齐高考文科数学第二次诊断性测验试卷
文科数学
(文科:必修+选修Ⅰ)
注意事项:
1.本卷分为问卷(共4页)和答卷(共4页),答案务必书写在答卷的指定位置处.
2.答卷前先将密封线内的项目填写清楚.
3.第Ⅰ卷(选择题,共12小题,共60分),在每小题的四个选项中,只有一项是符合题目要求的.如果选用答题卡,每小题选出答案后,用![]() 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案;如果未选用答题卡请将所选项前的字母代号填写在答卷上.不要答在问卷上.
铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案;如果未选用答题卡请将所选项前的字母代号填写在答卷上.不要答在问卷上.
4. 第Ⅱ卷(非选择题,共10小题,共90分),用钢笔或圆珠笔直接答在问卷中.
第Ⅰ卷(选择题 共60分)
一、选择题(共12小题,每小题5分,共60分)
1.![]() 的最小正周期为
的最小正周期为
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设两个不相等的非空集合![]() ,
,![]() ,那么“
,那么“![]() ”是“
”是“![]() ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.在公差为![]() 的等差数列
的等差数列![]() 中,
中,![]() 成等比数列,则
成等比数列,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 实数![]() 满足约束条件
满足约束条件 的最小值是
的最小值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
5.
若函数![]() 满足
满足![]()
![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.从正方体的八个顶点中任取四个点,在能构成的一对异面直线中,其所成的角的度数不可能是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]() 的导函数为
的导函数为![]() ,则
,则![]() 的单调增区间是
的单调增区间是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
![]()
8.![]() 的反函数是
的反函数是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.一束光线从点![]() 发出并经
发出并经![]() 轴反射,到达圆
轴反射,到达圆![]() 上一点的最短路程是
上一点的最短路程是
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
10.与直线![]() 垂直的抛物线
垂直的抛物线![]() 的切线方程是
的切线方程是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.若椭圆上一点与其中心及长轴的一个端点构成等腰直角三角形,则此椭圆的离心率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.三个半径为![]() 的球互相外切,且每个球都同时与另两个半径为
的球互相外切,且每个球都同时与另两个半径为![]() 的球外切.如果这两个半径为
的球外切.如果这两个半径为![]() 的球也互相外切,则
的球也互相外切,则![]() 与
与![]() 的关系是
的关系是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择题 共90分)
二、填空题(共4小题,每小题5分,共20分)请将答案直接填在答卷的相应各题的横线上.
13.若向量![]() 、
、![]() 满足
满足![]() ,
,![]() 且
且![]() ,则
,则![]() 与
与![]() 的夹角的度数为 .
的夹角的度数为 .
14.已知△![]() 的面积等于
的面积等于![]() 最大边
最大边![]() ,
,![]() ,则
,则![]()
![]() .
.
15.某校要求每位学生从![]() 门课程中选修
门课程中选修![]() 门,其中甲、乙两门课程至少选修一门,则不同的选课方案有
种(以数字作答).
门,其中甲、乙两门课程至少选修一门,则不同的选课方案有
种(以数字作答).
16.已知![]() 的展开式中的常数项为
的展开式中的常数项为![]() ,则非零实数
,则非零实数![]() 的值是 .
的值是 .
三、解答题(共6小题,共70分)解答应在答卷的相应各题中写出文字说明,证明过程或演算步骤.
17.(本题满分10分)
已知![]() ,其中
,其中![]() ,求
,求![]() 的值.
的值.
18.(本题满分12分)
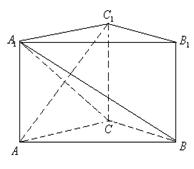 如图直三棱柱
如图直三棱柱![]() 的底面是等腰直角三角形,
的底面是等腰直角三角形,![]() ,且二面角
,且二面角![]() 的度数为
的度数为![]() °
°
(1)求![]() 的长;
的长;
(2)求证![]() 平面
平面![]() .
.
19.(本题满分12分)
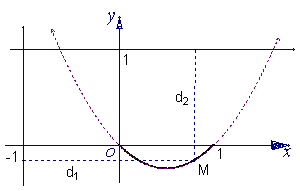
函数![]()
![]() ,
,![]() 、
、![]() 是其图象上任意不同的两点.
是其图象上任意不同的两点.
(1)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)求函数![]() 图象上一点
图象上一点![]() 到直线
到直线![]() 、 直线
、 直线![]() 距离之积的最大值.
距离之积的最大值.
20.(本题满分12分)
同时抛掷两个骰子(各个面上分别标以数![]() ),求
),求
(1) 向上的数都是![]() 的倍数的概率;
的倍数的概率;
(2)向上的数之和是![]() 的倍数的概率.
的倍数的概率.
21.(本题满分12分)
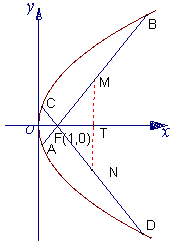
已知抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() 、
、![]() ,设
,设![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() .
.
(1)求证直线![]() 恒过定点;
恒过定点;
(2)求![]() 的最小值.
的最小值.
22.(本题满分12分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() (
(![]() 为常数),且
为常数),且![]() ,
,![]() .
.
(1)求![]() 的值,及数列
的值,及数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的最大值.
的最大值.
参考答案及评分标准
一、选择题(共12小题,每小题5分,共60分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选 项 |
|
|
|
|
|
|
|
|
|
|
|
|
1.选C.![]() ∴
∴![]() .
.
2.选B.根据题意有![]() .
.
3.选A.根据题意,有![]()
![]() ,解得
,解得![]() .
.
4.选A.
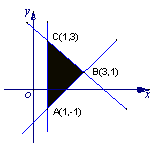 在A(1,-1)处目标函数达到最小值1.
在A(1,-1)处目标函数达到最小值1.
5.选D.![]() .
.
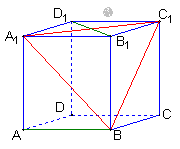 6.选A.两条棱所在直线异面时所成角的度数是
6.选A.两条棱所在直线异面时所成角的度数是![]() ;面对角线与棱异面时所成角的度数是
;面对角线与棱异面时所成角的度数是![]() 或
或![]() ;两条面对角线异面时所成角的度数是
;两条面对角线异面时所成角的度数是![]() 或
或![]() ;体对角线与棱所在直线异面时所成角的度数是
;体对角线与棱所在直线异面时所成角的度数是![]() ;体对角线与面对角线异面时所成角的度数是
;体对角线与面对角线异面时所成角的度数是![]() .
.
7.选C.当![]() ,即
,即![]() 时,
时,![]() 单调递增.
单调递增.
8.选B.![]()
![]()
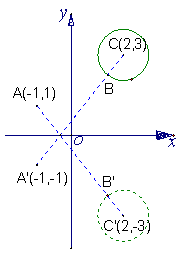 9.选A.原问题可转化为:点
9.选A.原问题可转化为:点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 到达圆
到达圆![]() 的最短路程,画图可知其值为
的最短路程,画图可知其值为
![]() .
.
10.选B.易知与直线![]() 垂直的直线方程的斜率是
垂直的直线方程的斜率是![]() ,设切点为
,设切点为![]() ,
,
则![]() 在此处的切线斜率是
在此处的切线斜率是![]() ,故
,故![]() ,∴
,∴![]()
∴所求切线方程是![]() .
.
11.选C.不妨设椭圆的方程为![]() ,由题意得椭圆上的点
,由题意得椭圆上的点![]() 坐标为
坐标为![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
12.选D.设![]() 分别是半径为
分别是半径为![]() 的三个球的球心,
的三个球的球心,
![]() 分别是半径为
分别是半径为![]() 的两个球的球心,则它们构成立体图形(如图),
的两个球的球心,则它们构成立体图形(如图),![]() 是△
是△![]() 的中心.因为△
的中心.因为△![]() 是边长为
是边长为![]() 的正三角形,
的正三角形,
所以,![]() .又
.又![]() 是以
是以![]() 为直角的直角三角形,
为直角的直角三角形,
故![]() ,即
,即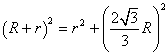 ,解得
,解得![]() .
.

二、填空题(共4小题,每小题5分,共20分)
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
13.由![]() ,得
,得![]() ,即
,即![]()
![]() ,又
,又![]() 故
故![]()
![]() ,
,
∴ ![]() ∴
∴![]() 与
与![]() 的夹角的度数为
的夹角的度数为![]() .
.
14.![]() ,即
,即![]()
![]() ,
,
∵![]() 是最大边,∴
是最大边,∴![]() 是最大角,故
是最大角,故![]() 不可能是钝角,∴
不可能是钝角,∴![]()
![]()
![]() , ∴
, ∴![]() .
.
15.从![]() 门课程中选修
门课程中选修![]() 门,有
门,有![]() 种方案;甲、乙两门课程都没选有
种方案;甲、乙两门课程都没选有![]() 种方案,故不同的选课方案有
种方案,故不同的选课方案有![]() 种.
种.
16.![]()
![]() ,令
,令![]() 得
得![]() ,所以常数项为
,所以常数项为![]() ,解得
,解得![]() .
.
三、解答题(共6小题,共70分)
17.![]()
![]() ,即
,即![]()
又![]() , ∴
, ∴![]() ,于是,
,于是,![]() 即
即![]()
∴![]() =
= =
=![]() . …10分
. …10分
18.解法一:
(1)由题意知![]() °,即
°,即![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]()
于是![]() 就是二面角
就是二面角![]() 的平面角且
的平面角且![]()
![]() °
°
在![]() 中,
中,![]() °,
°,![]() ,∴
,∴![]()
![]() …6分
…6分
(2)由(1)知![]() 是正方形,
是正方形,![]() ,又
,又![]() 是直棱柱且
是直棱柱且![]()
∴![]() 平面
平面![]() ,于是
,于是![]() ,故
,故![]() 平面
平面![]() .
…12分
.
…12分
解法二:
(1) 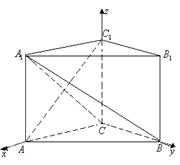 由题意知
由题意知![]() °,又
°,又![]() 是直棱柱
是直棱柱
设![]() ,如图建立直角坐标系易知
,如图建立直角坐标系易知
![]()
于是![]() ,
, ![]() ,
,![]() ,
,
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() 由
由 ,得
,得 ![]() ,取
,取![]()
所以![]() ,则
,则![]()
由于二面角![]() 等于
等于![]() °∴
°∴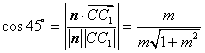 ,
,
得![]() ∴
∴![]()
![]() …6分
…6分
(2)由(1)得![]() ,
,![]() ,易知
,易知![]() ,故
,故![]()
![]() ,故
,故![]() ∴
∴![]() 平面
平面![]() .
…12分
.
…12分
19.设![]() 、
、![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,则
,则![]() ,
,![]()
于是,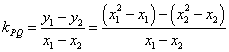 =
=![]() =
=![]()
∵![]() 且
且![]() , ∴
, ∴![]() .
.
故直线![]() 斜率的取值范围是
斜率的取值范围是![]() .
…5分
.
…5分
(2)设点![]() ,其中
,其中![]() ,则
,则![]() 到直线
到直线![]() 的距离
的距离![]()
![]() 到直线
到直线![]() 的距离
的距离![]()
则![]()
![]() =
=![]() =
=![]()
![]() ,当
,当![]() 时,
时,![]() ,
,![]() 递增
递增
当![]() 时,
时,![]() ,
,![]() 递减;
递减;
∴当![]() 时,
时,![]() 有最大值
有最大值![]() .
…12分
.
…12分
20.
(1)此题看作先后抛掷两个骰子,若用有序数组![]() 表示这个试验的结果,其中
表示这个试验的结果,其中
![]() ,
,![]() 分别表示先后掷出的点数,此时共有以下
分别表示先后掷出的点数,此时共有以下![]() 种情形:
种情形:![]() 、
、 ![]() 、
、![]() 、
、
![]() ,而试验所包含的结果总数为
,而试验所包含的结果总数为![]() ∴
∴![]() . …5分
. …5分
(2)此时共有以下![]() 种情形:
种情形:![]() 、
、 ![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,而试验所包含的结果总数为
,而试验所包含的结果总数为![]()
∴![]() .
…12分
.
…12分
21.(1)由题意可知直线![]() 、
、![]() 的斜率都存在且不等于零,
的斜率都存在且不等于零,![]() .
.
设![]() ,代入
,代入![]() ,得
,得![]()
∴![]() ,
,![]() ,故
,故 .
.
因为![]() ,所以,将点
,所以,将点![]() 坐标中的
坐标中的![]() 换为
换为![]() ,得
,得![]()
① 当![]() 时,则
时,则 ,
,
即![]() 此时直线
此时直线![]() 恒过定点
恒过定点![]() ;
;
②
当![]() 时,
时,![]() 的方程为
的方程为![]() ,也过
,也过![]() 点.
点.
故不论![]() 为何值,直线
为何值,直线![]() 恒过定点
恒过定点![]() .
…7分
.
…7分
(2)由(1)知 ,
,![]() ,
,
∴![]()

![]()
![]()

![]()
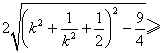

当且仅当![]() ,即
,即![]() 时,上式取等号,此时
时,上式取等号,此时![]() 的最小值是
的最小值是![]() . …12分
. …12分
22.
(1)当![]() 时,
时,![]() ,可得
,可得![]() 或
或![]()
若![]() ,由已知
,由已知![]() ,得
,得![]() ,与已知矛盾,故
,与已知矛盾,故![]() .
.
当![]() 时,则
时,则![]() ,又
,又![]() ,故
,故![]() ,所以
,所以![]() .
.
由![]() ,得
,得![]() ∴
∴![]() (
(![]() ),
),
当![]() 时,
时,![]() =
=![]()
![]() =
=![]() -
-![]()
化简得:![]() ,即
,即![]() ,所以
,所以![]() 为等差数列.
为等差数列.
∴![]() .
…6分
.
…6分
(2)∵![]()
![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]() …12分
…12分
以上各题的其它解法,限于篇幅从略,请相应评分.