08高考理科数学2月模拟考试试题
数学理科
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,总分150分,考试时间120分钟。
第Ⅰ卷(选择题,共55分)
一、选择题(本大题共11小题,每小题5分,共55分)
1.复数![]() =
=
A.-i B.I C.2![]() -i D.-2
-i D.-2![]() +i
+i
2.函数的y=![]() (x≤-1)反函数是
(x≤-1)反函数是
A.y=-![]() (x≥0) B.y=
(x≥0) B.y=![]() (x≥0)
(x≥0)
C.y=-![]() (x≥
(x≥![]() ) D.y=
) D.y=![]() (x≥
(x≥![]() )
)
3.若函数f (x)=e xcosx,则此函数图象在点(1, f (1))处的切线的倾斜角为
A.0 B.锐角 C.![]() D.钝角
D.钝角
 4.在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为
4.在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.曲线y=2sin![]() 和直线在y=
和直线在y=![]() 在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则P2P4等于
在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则P2P4等于
A.![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
6.已知α、β是平面,m、n是直线,则下命题不正确的是
A.若m∥n , m⊥α, 则n⊥α B.若,m⊥α, m⊥β, 则α∥β
C.若m⊥α, m∥n, n![]() β, 则α⊥β D.若m∥α, α
∩β=n则m∥n
β, 则α⊥β D.若m∥α, α
∩β=n则m∥n
7.设函数f
(x)是定义在R上的以5为周期的奇函数,若f (2)>1,f (2008)=![]() ,则a的取值范围是
,则a的取值范围是
A.(-∞, 0) B.(0, 3)
C.(0, +∞) D.(-∞, 0)∪(3, +∞)
8.设f
(x)= x2-6x+5,若实数x、y满足条件f (y)≤ f (x)≤0,则![]() 的最大值为
的最大值为
A.9-4![]() B.1 C.3 D.5
B.1 C.3 D.5
9.已知点A,
F分别是椭圆![]() (a>b>0)的右顶点和左焦点,点B为椭圆短轴的一个端点,若
(a>b>0)的右顶点和左焦点,点B为椭圆短轴的一个端点,若![]() =0,则椭圆的离心率e为
=0,则椭圆的离心率e为
A.![]() (
(![]() -1) B.
-1) B.![]() (
(![]() -1) C.
-1) C.![]() D.
D.![]()
10.在圆周上有10个等分,以这些点为顶点,每3个点可以构成一个三角形,如果随机选择了3个点,刚好构成直角三角形的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知集合P={x5x-a≤0}, Q={x6x-b>0},a, b∈N, 且A∩B∩N={2,3,4},则整数对(a, b)的个数为
A.20 B.30 C.42 D.56
第Ⅱ卷(非选择题, 共95分)
二、填空题(每小题4分,共16分)
12.![]() 的展开式中的常数项等于
;
的展开式中的常数项等于
;
13.已知![]() =1,
=1,![]() =
=![]() ,
,![]() ·
·![]() =0, 点C在∠AOB内,且∠AOC=30°,设
=0, 点C在∠AOB内,且∠AOC=30°,设![]() =m
=m![]() +n
+n![]() ( m, n∈R), 则m/n等于
;
( m, n∈R), 则m/n等于
;
14.编辑一个运行程序:1﹡1=x,,m﹡(n+1)=k+2,欲得到1﹡2007=2008的输出结果,则x的值为 ;
15.已知函数f (x)=![]() -log2x正实数a、b、c成公差为正数的等差数列,且满足f (a) f (b)f
(c)<0,若实数d是方程f
(x)=0的一个解,那么下列四个判断:
-log2x正实数a、b、c成公差为正数的等差数列,且满足f (a) f (b)f
(c)<0,若实数d是方程f
(x)=0的一个解,那么下列四个判断:
① d<a; ②d>b; ③d<c; ④d>c中有可能成立的为 (填序号).
三、解答题(本大题共6小题,共79分)
16.(本小题满分12分)
设函数f (x)=2cosx (cosx+![]() sinx)-1,x∈R
sinx)-1,x∈R
(1)求f (x)的最小正周期T;
(2)求f (x)的单调递增区间.
17.(本小题满分13分)
某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提高通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是,且每题正确完成与否互不影响.求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
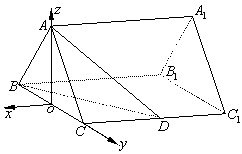
18.(本小题满分14分)
 如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
如图,正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
(1)求此正三棱柱的侧棱长;
(2)求二面角A-BD-C的大小;
(3)求点C到平面ABD的距离.
19.(本小题满分14分)
已知数列{an}中,an=2-![]() ( n≥2,n∈N+)
( n≥2,n∈N+)
(1)若a1=![]() ,数列{bn}满足bn=
,数列{bn}满足bn=![]() ( n∈N+),求证数列{bn}是等差数列;
( n∈N+),求证数列{bn}是等差数列;
(2)若a1=![]() ,求数列{an}中的最大项与最小项,并说明理由.
,求数列{an}中的最大项与最小项,并说明理由.
(3)若1<a1<2, 试证:1<an+1< an<2
20.(本小题满分12分)
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=![]() x2的焦点,离心率等于
x2的焦点,离心率等于![]() .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若![]() =λ1
=λ1![]() ,
,![]() =λ2
=λ2![]() ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.
21.(本小题满分14分)
已知函数f (x)=ln(2+3x)-![]() x2 .
x2 .
(1)求f (x)在[0, 1]上的极值;
(2)若对任意x∈[![]() ,
,![]() ],不等式a-lnx-ln[ f
’(x)+3x]>0成立,求实数a的取值范围;
],不等式a-lnx-ln[ f
’(x)+3x]>0成立,求实数a的取值范围;
(3)若关于x的方程f (x)= -2x+b在[0, 1]上恰有两个不同的实根,求实数b的取值范围.
参考答案
一、选择题:本大题共11小题,每小题5分,共55分.
1.B 2.A 3.D 4.C 5.A 6.D 7.B 8.D 9.A 10.C
11.B
二、填空题:本大题共4小题,每小题4分,共16分.
12.-32; 13.3; 14.-2004; 15.①②③
三、解答题:本大题共6小题,共79分.
16.![]() ………… 6分
………… 6分
(1)![]() .
………… 9分
.
………… 9分
(2)由2kp – ![]() £ 2x +
£ 2x + ![]() £ 2kp +
£ 2kp + ![]() , 得:kp –
, 得:kp – ![]() £ x £ kp +
£ x £ kp + ![]() (k ÎZ),
(k ÎZ),
f ( x ) 单调递增区间是[kp – ![]() ,kp +
,kp +![]() ](k ÎZ). ……………… 12分
](k ÎZ). ……………… 12分
17.(1)设考生甲、乙正确完成实验操作的题数分别为![]() 、
、![]() ,
,
则![]() 取值分别为1,2,3;
取值分别为1,2,3;![]() 取值分别为0,1,2,3。…………………………2分
取值分别为0,1,2,3。…………………………2分
![]() ,
,![]() ,
,![]() 。
。
∴考生甲正确完成题数的概率分布列为
|
| 1 | 2 | 3 |
|
|
|
|
|
……………………………4分
![]() 。……………………………………………………5分
。……………………………………………………5分
∵![]()
![]() ,
,
同理:![]() ,
,![]() ,
,![]() 。
。
∴考生乙正确完成题数的概率分布列为:
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
………………………8分
![]() 。…………………………………9分
。…………………………………9分
(2)∵![]() ,
,
![]() 。
。
(或![]() )。∴
)。∴![]() 。
。
∵![]() ,
,![]() ,
,
∴![]() 。
。
从做对题数的数学期望考察,两人水平相当;从做对题数的方差考察,甲较稳定;从至少完成2题的概率考察,甲获得通过的可能性大。因此可以判断甲的实验操作能力较强。…………………………………………………………………………………………13分
说明:只根据数学期望与方差得出结论,也给4分。
18.(1)设正三棱柱![]() —
—![]() 的侧棱长为
的侧棱长为![]() .取
.取![]() 中点
中点![]() ,连
,连![]() .
.

![]() 是正三角形,
是正三角形,![]() .
.
又底面![]() 侧面
侧面![]() ,且交线为
,且交线为![]() .
.
![]() 侧面
侧面![]() .
.
连![]() ,则直线
,则直线![]() 与侧面
与侧面![]() 所成的角为
所成的角为![]() .
.
在![]() 中,
中, ,解得
,解得![]() .
.
![]() 此正三棱柱的侧棱长为
此正三棱柱的侧棱长为![]() .
……………………5分
.
……………………5分
注:也可用向量法求侧棱长.
(2)解法1:过![]() 作
作![]() 于
于![]() ,连
,连![]() ,
,
![]() 侧面
侧面![]()
![]()
![]() .
.![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,
又 ,
,![]()
![]() .
.
又![]()
![]() 在
在![]() 中,
中,![]() .
.
故二面角![]() 的大小为
的大小为![]() .
………………………10分
.
………………………10分
解法2:(向量法,见后)
(3)解法1:由(2)可知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
![]() 过
过![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() .
.
在![]() 中,
中,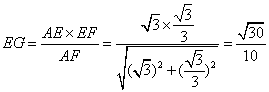 .
.
![]()
![]() 为
为![]() 中点,
中点,![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() . …………14分
. …………14分
解法2:(思路)取![]() 中点
中点![]() ,连
,连![]() 和
和![]() ,
,
由![]()
![]() ,易得平面
,易得平面![]() 平面
平面![]() ,且交线为
,且交线为![]() .
.
过点![]() 作
作![]() 于
于![]() ,则
,则![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离.
的距离.
 解法3:(思路)等体积变换:由
解法3:(思路)等体积变换:由![]() 可求.
可求.
解法4:(向量法,见后)
题(Ⅱ)、(Ⅲ)的向量解法:
(2)解法2:如图,建立空间直角坐标系![]() .
.
则![]() .
.
设![]()
![]() 为平面
为平面![]() 的法向量.
的法向量.
由 得
得![]()
 .取
.取![]()
又平面![]() 的一个法向量
的一个法向量![]()
![]()
 .
.
结合图形可知,二面角![]() 的大小为
的大小为![]() . …………10分
. …………10分
(3)解法4:由(Ⅱ)解法2,![]()
![]()
![]() 点
点![]() 到平面
到平面![]() 的距离
的距离
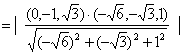 =
=![]() .
.
14分
19.(1) ,而
,而![]() ,
,
∴![]() .
.![]()
∴{![]() }是首项为
}是首项为![]() ,公差为1的等差数列.
………………… 5分
,公差为1的等差数列.
………………… 5分
(2)依题意有![]() ,而
,而![]() ,∴
,∴![]() .
.
对于函数![]() ,在x>3.5时,y>0,且在(3.5,
,在x>3.5时,y>0,且在(3.5,![]() )上为减函数.
)上为减函数.
故当n=4时,![]() 取最大值
取最大值![]() =3.
=3.
而函数![]() 在x<3.5时,y<0,且在(
在x<3.5时,y<0,且在(![]() ,3.5)上也为减函数.
,3.5)上也为减函数.
故当n=3时,![]() 取最小值
取最小值![]() =-1.
…………………… 9分
=-1.
…………………… 9分
(3)先用数学归纳法证明![]() ,再证明
,再证明![]() .
.
①当![]() 时,
时,![]() 成立;
成立;
②假设当![]() 时命题成立,即
时命题成立,即![]() ,
,
当![]() 时,
时,![]()
![]()
![]()
![]()
故当![]() 时也成立,
时也成立,
综合①②有,命题对任意![]() 时成立,即
时成立,即![]() .
.
(也可设![]() (1≤
(1≤![]() ≤2),则
≤2),则![]() ,
,
故![]()
![]()
![]() ). ………………… 12分
). ………………… 12分
下证:![]()
![]()
![]()
![]() .
.
所以,![]() 成立 。
………………… 14分
成立 。
………………… 14分
20.(1)设椭圆C的方程为![]() ,则由题意知b = 1.
,则由题意知b = 1.
![]()
∴椭圆C的方程为 ![]() …………………………………………………5分
…………………………………………………5分
(2)方法一:设A、B、M点的坐标分别为![]()
易知F点的坐标为(2,0).
![]() ,
,![]()
将A点坐标代入到椭圆方程中,得![]()
去分母整理得![]() ………………………………………10分
………………………………………10分
![]()
![]()
![]() …………………………………………………………12分
…………………………………………………………12分
方法二:设A、B、M点的坐标分别为![]()
又易知F点的坐标为(2,0).
显然直线l存在的斜率,设直线l的斜率为k,则直线l的方程是![]()
将直线l的方程代入到椭圆C的方程中,消去y并整理得
![]() ……………………………………7分
……………………………………7分
![]() ……………………………………8分
……………………………………8分
又![]()
![]() …………12分
…………12分
21.(1)![]() ,
,
令![]() (舍去)
(舍去)
![]() 单调递增;
单调递增;
当![]() 单调递减.
单调递减.
∴函数![]() 在
在![]() 上有极大值
上有极大值![]()
(2)由![]() 得
得
![]() , …………①
, …………①
设![]() ,
,![]() ,
,
依题意知![]() 上恒成立,
上恒成立,
![]() ,
,
![]() ,
,
![]() 上单增,要使不等式①成立,
上单增,要使不等式①成立,
当且仅当![]() …………… 10分
…………… 10分
(3)由![]()
令![]() ,
,
当![]() 上递增;
上递增;
当![]() 上递减
上递减
而![]() ,
,
![]() 恰有两个不同实根等价于
恰有两个不同实根等价于

所以,![]() . ………………
14分
. ………………
14分