08高考数学质量检测试题
数学试题
试卷说明:本试卷分选择题和非选择题两部分,满分150分.考试用时120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。
1. (仅文科做)一粒骰子,抛掷一次,得到奇数的概率是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
(仅理科做)若复数![]() 为虚数单位.)是纯虚数,则实数
为虚数单位.)是纯虚数,则实数![]() 的值为( )
的值为( )
A.-6 B.![]() C.-2 D.6
C.-2 D.6
 2. 设
2. 设![]() ,
,![]() (0,1),则满足条件0≤
(0,1),则满足条件0≤![]() ≤1,0≤
≤1,0≤![]() ≤1的动点P的变化范围(图中阴影部分含边界)是 ( )
≤1的动点P的变化范围(图中阴影部分含边界)是 ( )
A B C D
3.已知椭圆的焦点是F1、F2,P是椭圆上的一个动点,过点F2向∠F1PF2的外角平分线作垂线,
垂足为M,则点M的轨迹是 ( )
A.圆 B.椭圆 C.直线 D.双曲线的一支
4.定义在R上的偶函数![]() 上是减函数,又
上是减函数,又![]() 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )
 A.
A. ![]() B.
B.![]()
C. ![]() D.
D.![]()
 5.如右图所示,△ADP为正三角形,四边形ABCD为正方形,
5.如右图所示,△ADP为正三角形,四边形ABCD为正方形,
平面PAD⊥平面ABCD.点M为平面ABCD内的一个动点,且满
足MP=MC.则点M在正方形ABCD内的轨迹为 ( )
A B C D
6.方程![]() 解的个数为( )
解的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
7. (仅文科做)有5个人拿着不同的水桶在一个水龙头前排队打水,前面的人接满后离开,后面的人才能继续接水. 甲接满水需1分钟,乙接满水需1.8分钟,丙接满水需1.5分钟,丁接满水需1.1分钟,戊接满水需1.2分钟.则所有人接水等待的时间总和的最小值为( )分钟.
A. 6.6 B. 14.6 C. 17.8 D. 19.8
(仅理科做)设随机变量![]() 服从正态分布N(0,1),
服从正态分布N(0,1),![]() 则
则![]() ( ) A.
( ) A.![]() P B.1-P
C.1-2P D.
P B.1-P
C.1-2P D.![]() -P
-P
8.若对![]() 时不等式
时不等式![]() 恒成立,则实数m的取值范围是 ( )
恒成立,则实数m的取值范围是 ( )
 A.(-2,3) B.(-3,3)
C.(-2,2) D.(-3,4)
A.(-2,3) B.(-3,3)
C.(-2,2) D.(-3,4)
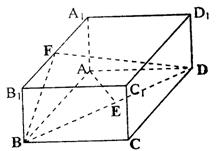
9.如图,正五边形ABCDE中,若把顶点A、B、C、D、E染上红、黄、绿
三种颜色中的一种,使得相邻顶点所染颜色不相同,则不同的染色方法
共有( )
A.30种 B.27种 C.24种 D.21种
10.设双曲线![]() 的半焦距为c,离心率为
的半焦距为c,离心率为![]() .若直线
.若直线![]() 与双曲线
与双曲线
的一个交点的横坐标恰为c,则k等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
记![]() 表示该表中第s行的第t个数,则表中的奇
表示该表中第s行的第t个数,则表中的奇
数2007对应于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
![]()

 12.小明为同学表演魔术,他用四张扑克牌摆成如图a
12.小明为同学表演魔术,他用四张扑克牌摆成如图a
形状,然后蒙上眼睛,请其他同学将其中一张牌颠倒
过来,当他睁开眼时,看见如图b形状,小明自称他
能解读牌中散发的特异能量,并准确地指出了同学动
 过的牌,你
过的牌,你 能试试哪张牌被动过吗?( )
能试试哪张牌被动过吗?( )


A.梅花5 B.黑桃6 C.红桃7 D.方块8
数学试题
注:请将选择题答案填入下表中,否则选择题计0分!
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分.
13.![]() 的展开式中常数项是
.
的展开式中常数项是
.
14. (仅文科做)设![]() .映射
.映射![]() 使
使
得B中的元素都有原象.则这样的映射![]() 有
个.
有
个.
(仅理科做)曲线![]() 在(1,0)点处的切方程为
.
在(1,0)点处的切方程为
.
15.已知实数 的最大值为
的最大值为
16.有下列四个命题: ①![]() 的必要不充分条件; ②若直线
的必要不充分条件; ②若直线![]()
![]() ; ③函数
; ③函数![]() 平移后得到的函数为
平移后得到的函数为![]() ; ④函数
; ④函数![]() 的最小正周期为
的最小正周期为![]() 。
。
其中真命题的序号为 (写出所有真命题的序号)。
三.解答题:本大题共6小题,满分74分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)在某次游艺活动中开展摸奖游戏,游戏规定:在装有黑球和红球的
箱子中,每次摸出一个球,若摸到红球,则中奖且摸奖结束;若摸到黑球则放回重摸,但每
人最多只能摸奖10次,已知每次摸到红球的概率为![]() .
.
(1)在摸奖游戏中,求某人摸奖不超过3次且中奖的概率;
(2)在摸奖游戏中,求某人10次摸奖机会全部用完的概率.
18. (本小题满分12分)已知函数![]() 为常数)的图象过点
为常数)的图象过点![]() 。 (1)求函数
。 (1)求函数![]() 的值域; (2)若函数y=f(x)的图像按向量
的值域; (2)若函数y=f(x)的图像按向量![]() 作长度最短的平移后,其图象关于y轴对称,求向量
作长度最短的平移后,其图象关于y轴对称,求向量![]() 的坐标。
的坐标。
19. (本小题满分12分)蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以![]() 表示第
表示第![]() 个图的蜂巢总数.
个图的蜂巢总数.

(1) 试给出![]() 的值,并求
的值,并求![]() 的表达式(不要求证明);
的表达式(不要求证明);
(2) 证明:![]() .
.
 20.(本小题满分12分)如图,已知长方体ABCD—A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角
20.(本小题满分12分)如图,已知长方体ABCD—A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角
为30°,AE⊥BD于E,F为A1B1的中点.
(1)求异面直线AE与BF所成角的余弦值;
(2)求平面BDF与平面A1B所成二面角(锐角)的正切值;
(3)(此问文科不做仅理科做)求点A到平面BDF的距离.
21. (本小题满分12分)(仅文科做)已知![]() 为椭圆
为椭圆![]()
![]() 的右焦点,直线
的右焦点,直线![]() 过点
过点![]() 且与双曲线
且与双曲线![]() 的两条渐近线
的两条渐近线![]() 分别交于点
分别交于点![]() ,与椭圆交于点
,与椭圆交于点![]() .
.
(1)若![]() ,双曲线的焦距为4。求椭圆方程。
,双曲线的焦距为4。求椭圆方程。
(2)若![]() (
(![]() 为坐标原点),
为坐标原点),![]() ,求椭圆的离心率
,求椭圆的离心率![]() 。
。
(仅理科做)已知椭圆C过点![]() 是椭圆的左焦点,P、Q是椭圆C上的两个动点,且PF、MF、QF成等差数列。 (1)求椭圆C的标准方程;
是椭圆的左焦点,P、Q是椭圆C上的两个动点,且PF、MF、QF成等差数列。 (1)求椭圆C的标准方程;
(2)求证:线段PQ的垂直平分线经过一个定点A;
(3)设点A关于原点O的对称点是B,求PB的最小值及相应点P的坐标。
22. (本小题满分14分)已知函数![]()
(1)![]() 上存在单调递增区间,求
上存在单调递增区间,求![]() 的取值范围。
的取值范围。
(2)若存在实数![]() ,是否存在实数
,是否存在实数![]() 处的切线斜率为0,若存在,求出一组实数a, b, c,若不存在,说明理由。
处的切线斜率为0,若存在,求出一组实数a, b, c,若不存在,说明理由。
数学试题参考答案及评分标准
一、选择题:本大题共12小题,每小题5分,共60分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | A | C | A | C | C | A | A | C | A | D |
二、填空题:本大题共4小题,每小题4分.
13. 20 14. (文科) 36 (理科) y=x-1 . 15. 14 16. ③
三、解答题:本大题共6小题,满分74分。解答应写出文字说明,证明过程或演算步骤。
17.解:⑴每次摸到的红球的概率为![]() ,则摸到黑球的概率为
,则摸到黑球的概率为![]() ,前3次中奖的概率
,前3次中奖的概率
![]() ……………………………………………………(6分)
……………………………………………………(6分)
⑵本次摸奖游戏中,未中奖的概率为![]() ,
,
那么恰在第10次中奖的概率为![]() ,10次摸奖机会全部用完的概率为
,10次摸奖机会全部用完的概率为
![]() ………………………………………(12分)
………………………………………(12分)
18.解:(1)因为函数![]() ………………………(2分)
………………………(2分)
![]() ,
,
![]() …………………………………………………………(6分)
…………………………………………………………(6分)
(2)设函数![]() 平移后的坐标为
平移后的坐标为![]()
则![]()
![]() ,其图像关于y轴对称,
,其图像关于y轴对称,
![]() ………………………(10分)
………………………(10分)
![]() ………………………(12分)
………………………(12分)
19. 解: ⑴![]() …………………………………………………(4分)
…………………………………………………(4分)
由于![]()
![]()
因此,当![]() 时,有
时,有![]()
所以![]()
![]() .
.
又![]() ,所以
,所以![]() . ……………………(7分)
. ……………………(7分)
(注:直接给出结果也给分)
⑵当![]() 时,
时,![]() . …………………(10分)
. …………………(10分)
所以![]()
![]() . ……………………………………………………(12分)
. ……………………………………………………(12分)
20.解:(1)连结B1D1,过F作B1D1的垂线,垂足为K. ∵BB1与两底面ABCD,A1B1C1D1都垂直.
![]()
![]() FK⊥BB1
又AE⊥BB1
FK⊥BB1
又AE⊥BB1
∴ FK⊥B1D1
![]() FK⊥平面BDD1B1,又AE⊥BD
FK⊥平面BDD1B1,又AE⊥BD ![]() AE⊥平面BDD1B1
,因此KF∥AE.
AE⊥平面BDD1B1
,因此KF∥AE.
B1D1∩BB1=B1 BB1∩BD=B
∴∠BFK为异面直线BF与AE所成的角, ………………………………(文科2分理科1分)
连结BK,由FK⊥面BDD1B1得FK⊥BK,从而△BKF为Rt△.
 在Rt△B1KF和Rt△B1D1A1中,由
在Rt△B1KF和Rt△B1D1A1中,由![]() 得:
得:

又BF=![]() .
. ![]()
∴异面直线BF与AE所成角的余弦值为![]() . …………………………(文科6分理科4分)
. …………………………(文科6分理科4分)
(2)由于DA⊥平面AA1B ,连结AF,易知BF⊥AF,由三垂线定理知BF⊥DF.
∴∠AGD即为平面BDF与平面AA1B所成二面角的平面角. ……………(文科8分理科6分)
![]() 在Rt△BAD中,AD=
在Rt△BAD中,AD=![]() 又AF=
又AF=![]() ,∴tan∠AFD=
,∴tan∠AFD=
故平面BDF与平面AA1B1B所成二面角(锐角)的正切值为![]() .……(文科12分理科8分)
.……(文科12分理科8分)
(3)由(2)知平面AFD是平面BDF与平面AA1B1B所成二面角的平面角所在的平面.
∴面AFD⊥面BDF.
在Rt△ADF中,由A作AH⊥DF于H,则AH即为点A到平面BDF的距离.
由AH·DF=AD·AF,得
所以点A到平面BDF的距离为![]() …………………………………………(理科12分)
…………………………………………(理科12分)
另解:(1)以A为坐标原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,则
A(0,0,0),A1(0,0,1),B(2,0,0),F(1,0,1), ![]() ,
,![]() ,
,
![]() ,
,![]()

∴异面直线BF与AE所成角的余弦值为![]() .……………………………(文科6分理科4分)
.……………………………(文科6分理科4分)
(2)取平面AA1B1B的法向量为![]() ,设平面BDF的法向量为
,设平面BDF的法向量为![]() ,
,
![]() ,
,![]() ,
,
由 ,即
,即 ,∴
,∴
取平面BDF的法向量为![]()
 ,即
,即![]()
故平面BDF与平面AA1B1B所成二面角(锐角)的正切值为![]() ………(文科12分理科8分)
………(文科12分理科8分)
(3) 设点A到平面BDF的距离为![]() ,取平面BDF的法向量为
,取平面BDF的法向量为![]() ,
,![]() ,
,
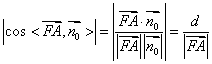 即
即
所以点A到平面BDF的距离为![]() ………………………………………(理科12分)
………………………………………(理科12分)
21. (文科)解:⑴![]() ,
,![]() 是直线
是直线![]() 与双曲线两条渐近线的交点,
与双曲线两条渐近线的交点,
![]() , 即
, 即![]() ……………………………………2分
……………………………………2分
![]() 双曲线的焦距为4,
双曲线的焦距为4,![]() …………………………………………4分
…………………………………………4分
解得,![]()
![]() 椭圆方程为
椭圆方程为![]() ………………………6分
………………………6分
⑵解:设椭圆的焦距为![]() ,则点
,则点![]() 的坐标为
的坐标为![]()
![]() ,
, ![]()
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,
![]() 直线
直线![]() 的方程为
的方程为![]() ……………………………………………………………8分
……………………………………………………………8分
由 解得
解得 即点
即点![]()
设![]() 由
由![]() , 得
, 得![]()
即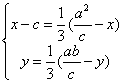

![]()
![]() 点
点![]() 在椭圆上,
在椭圆上,![]() …………………………………………10分。
…………………………………………10分。
![]()
![]() ,
,![]()
∴![]() ∴
∴![]()
![]() ∴椭圆的离心率是
∴椭圆的离心率是![]() 。 ……………………………12分
。 ……………………………12分
21. (理科)解:(1)设椭圆C的方程为![]() ,
,
由已知,得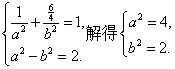
所以椭圆的标准方程为![]() ……………………………………………3分
……………………………………………3分
(2)证明:设![]() 知
知
![]()
同理![]()
![]()
![]() ………………………………………………………………………4分
………………………………………………………………………4分
①当 ,
,
从而有![]()
设线段PQ的中点为![]() ,
,
得线段PQ的中垂线方程为![]()
![]() ………………………………6分
………………………………6分
②当![]()
线段PQ的中垂线是x轴,也过点![]()
![]() ……………………………………………8分
……………………………………………8分
(3)由![]()
![]() , ……10分
, ……10分
![]() ……………………………………12分
……………………………………12分
22.解:(1)当![]() ………………………………………2分
………………………………………2分
![]() 上存在单调递增区间,即
上存在单调递增区间,即![]() 上存在子区间使
上存在子区间使![]()
(i)当![]() 是开口向上的抛物线,
是开口向上的抛物线,
显然![]() 上存在区间使
上存在区间使![]() 适合 …………………4分
适合 …………………4分
(ii)当![]() 是开口向下的抛物线,
是开口向下的抛物线,
要使![]() ,
,
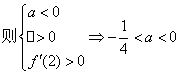 …………………………………………………7分
…………………………………………………7分
![]() ………………………………………………8分
………………………………………………8分
(2)不存在实数a, b, c满足题设条件,
事实上,由![]()

故不存在实数a, b, c满足题设条件。 ………………………………………14分
注:以上答案及评分标准仅供参考,如有其它解法请酌情给分!