08高考数学(理科)教学质量调研监测
数学试题(理科)
命题:余永安 审题:孙彦
(考试用时120分钟,满分阶150分。)
第Ⅰ卷(选择题,共55分)
一、选择题(本大题共11小题,每小题5分,共55分。在每小题列出的四个选项中,只有一项是最符合题目要求的。)
1.若全集U=![]() 且CUA=
且CUA=![]()
![]() ,则集合A的真子集共有
,则集合A的真子集共有
A.3个 B.5个 C.7个 D.8个
2.函数f(x)=2-x(x>0)的反函数f-1(x)=
A.-log2(x)(x>0) B.log2(-x)(x<0)
C.-log2(x)(0<x<1) D.log2(-x)(-1<x<0)
 3.200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为
3.200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为
A.65辆 B.75辆
C.88辆 D.95辆
4.如常数a<-1,则数列 的极限等于
的极限等于
A.0 B.1 C.-1 D.2
5.已知两点M(-2,0),N(2,0),点P满足![]() ·
·![]() =0.则P的轨迹方程为
=0.则P的轨迹方程为
A.![]() + y2=1 B.x2 + y2=4 C.y2 _ x2=8 D.x2 + y2=8
+ y2=1 B.x2 + y2=4 C.y2 _ x2=8 D.x2 + y2=8
6.函数y=cotx的导数是
A.![]() =
=![]() B.
B.![]() = -
= - ![]() C.
C.![]() = -
= - ![]() D.
D.![]() =
=![]()
7.如果数列![]() 满足a1,
满足a1,![]() ,
,![]() , …,
, …,![]() ,…是首项为1,公比为2的等比数列,则a100等于
,…是首项为1,公比为2的等比数列,则a100等于
A.100 B.299 C.25050 D.24950
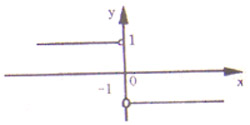 8.函数y=f(x)图像如右图所示,则不等式(x2-2x-8)f(x)>0的解为
8.函数y=f(x)图像如右图所示,则不等式(x2-2x-8)f(x)>0的解为
A.(0,4)![]()
B.(0,4)![]()
C.![]()
D.(-2,4)
9.将函数f(x)=log2(x+1)-1的图像按向量(1,1)平移后得到g(x)的表达式为
A.g(x)=log2(x+2) B.g(x)=log2x
C.g(x)=log2x-2 D.g(x)=log2x+2
10.连掷两次骰子分别得到点数m、n,则向量(m,n)与向量(-1,1)的夹角![]() >900的概率是
>900的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知函数y=f(x)和y=g(x)在![]() 的图像如图所示,给出下列四个命题:
的图像如图所示,给出下列四个命题:
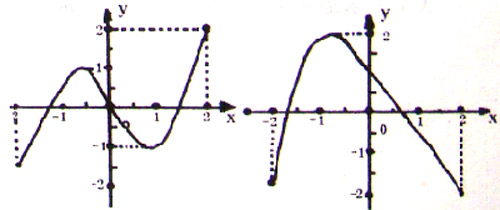
(1)方程f![]() =0有且仅有6个根;
=0有且仅有6个根;
(2)方程f![]() =0有且仅有3个根;
=0有且仅有3个根;
(3)方程f![]() =0有且仅有5个根;
=0有且仅有5个根;
(4)方程g![]() =0有且仅有4个根;
=0有且仅有4个根;
其中正确的命题个数是
A.4个 B.3个 C.2个 D.1个
第Ⅱ卷(非选择题,共95分)
二、填空题(本大题共4小题,每小题4分,共16分。把答案填在答题卡的相应位置)
12.在复平面内,复数z=![]() 对应的点位于第
象限;
对应的点位于第
象限;
13.函数y=![]() 的定义域是
的定义域是
14.已知实数x,y满足不等式组 ,那么目标函数Z=x+3y的最大值是
,那么目标函数Z=x+3y的最大值是
15.已知函数f(x)= 在x=1处连续,则实数a的值为
在x=1处连续,则实数a的值为
三、解答题(本大题共6小题,共79分。解答应写出文字说明、证明过程和演算步骤)
16.(本小题满分12分)
已知f(x)=![]() ,若数列
,若数列![]() 的首项a1=-3,
的首项a1=-3,![]() ,它的前n项和为
,它的前n项和为![]() .
.
(1)求通项公式an:
(2)求当n 为何值时![]() 取最小值。
取最小值。
17.(本小题满分13分)
已知函数![]()
(1)求函数f(x)的单调减区间;
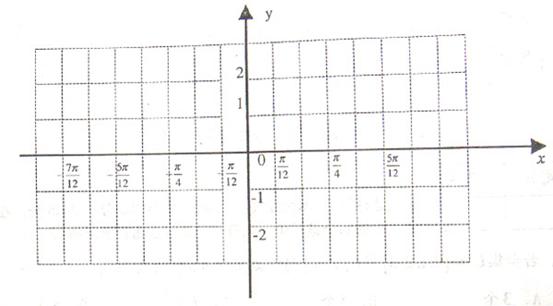
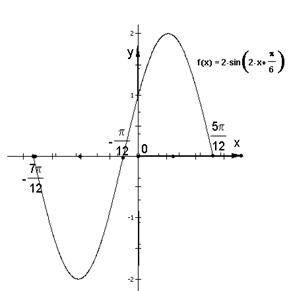
(2)画出函数g(x)=f(x),![]() 的图像,由图像研究并写出g(x)的对称轴和对称中心。
的图像,由图像研究并写出g(x)的对称轴和对称中心。
18.(本小题满分14分)
已知函数f(x)=![]() 的最大值不大于
的最大值不大于![]() ,又当
,又当![]() 时,
时,![]() ,求a的值。
,求a的值。
19.(本小题满分13分)
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,记![]()
(1)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量![]() 的分布列和数学期望。
的分布列和数学期望。
20.(本小题满分13分)
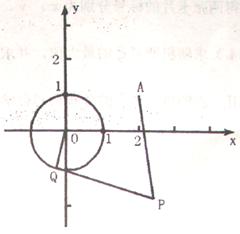
已知,如图⊙O:x2+y2=1和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足PQ=PA.
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。
21.(本小题满分14分)
定义域R的偶函数f(x),当x>0时,![]() ,方程f(x)=0在R上恰有5个不同的实数解。
,方程f(x)=0在R上恰有5个不同的实数解。
(1)求x<0时,函数f(x)的解析式;
(2)求实数a的取值范围。
安庆市2007-2008学年度教学质量调研监测
高三数学试题(理科)参考答案
一、选择题:(本大题共11小题,每小题5分,共55分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 | C | C | B | C | B | C | D | B | B | A | B |
二、填空题:(本大共4小题,每小题4分,共16分)
12.I 13.![]() 14.4 15.1
14.4 15.1
三、解答题:(本大题共6小题,共79分)
16、(本小题满分12分)
(1)由 ![]() 得:
得:![]() ,∴
,∴![]() ………3分
………3分
![]() =
=![]() ,
,![]()
∴![]() 为以
为以![]() 为首项,公差为
为首项,公差为![]() 的等差数列。
的等差数列。
![]() ………………6分
………………6分
(2)由 ,得
,得![]() ………………9分
………………9分
又![]() ,∴当
,∴当![]() 时,
时,![]() 取最小值。………………12分
取最小值。………………12分
17、(本小题满分13分)
(1)![]() ………………3分
………………3分
由![]() 得
得![]() ,
,
所以,函数f(x)减区间为![]() ………………6分
………………6分
(2)列表如下:
| T=2x+ | -π | - | 0 |
| π |
| x |
|
|
|
|
|
| Y=2sin( | 0 | -2 | 0 | 2 | 0 |
 …………9分
…………9分
(2)![]() 无对称轴,对称中心为(
无对称轴,对称中心为(![]() ) …………13分
) …………13分
18、(本小题满分14分)
![]() ,
,
![]() …………3分
…………3分
对称轴![]() ,当
,当![]() 时,
时,![]() 是
是![]() 的递减区间,而
的递减区间,而![]() ,
,
即![]() 与
与![]() 矛盾,即不存在;…………8分
矛盾,即不存在;…………8分
当![]() 时,对称轴
时,对称轴![]() ,而
,而![]() ,且
,且 …………11分
…………11分
即![]() ,而
,而![]() ,即
,即![]()
∴![]() …………14分
…………14分
19、(本小题满分13分)
(1)![]() 、
、![]() 可能的取值为
可能的取值为![]() 、
、![]() 、
、![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,且当
,且当![]() 或
或![]() 时,
时,![]() . ……………3分
. ……………3分
因此,随机变量![]() 的最大值为
的最大值为![]() .
.
![]() 有放回抽两张卡片的所有情况有
有放回抽两张卡片的所有情况有![]() 种,∴
种,∴![]() . …………5分
. …………5分
(2)![]() 的所有取值为
的所有取值为![]() .
.![]() 时,只有
时,只有![]() 这一种情况,
这一种情况,
![]() 时,有
时,有![]() 或
或![]() 或
或![]() 或
或![]() 四种情况,
四种情况,
![]() 时,有
时,有![]() 或
或![]() 两种情况.
两种情况.
∴![]() ,
,![]() ,
,![]() .
…………11分
.
…………11分
则随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
因此,数学期望![]() . ………………13分
. ………………13分
20、(本小题满分13分)
(1)连OP,![]() 为切点,PQ⊥OQ,由勾股定理有
为切点,PQ⊥OQ,由勾股定理有 ![]()
又由已知![]()
即:![]()
化简得实数a、b间满足的等量关系为:![]() ……………………5分
……………………5分
(2)由![]() ,得b=-2a+3。
,得b=-2a+3。
![]()
![]()
![]()
故当![]() ,即线段PQ长的最小值为
,即线段PQ长的最小值为![]() …………10分
…………10分
(3)设⊙P的半径为R,⊙P与⊙O有公共点,
∵⊙O的半径为1,∴![]()
而![]()
![]()
故当![]()
得半径取最小值⊙P的方程为![]() …………13分
…………13分
21、(本小题满分14分)
(1)设x<0,则-x>0∵![]() 为偶函数,∴
为偶函数,∴![]() ………3分
………3分
(2)方法一:∵![]() 为偶函数,∴
为偶函数,∴![]() =0的根关于x=0对称.
=0的根关于x=0对称.
由![]() =0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根.且两个正根和二个负根互为相反数
=0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根.且两个正根和二个负根互为相反数
∴原命题可转化为:![]() 图像与x轴恰有两个不同的交点 ………6分
图像与x轴恰有两个不同的交点 ………6分
下面研究当x>0时的情况:
∵![]() ∴
∴![]() …………9分
…………9分
即![]() 为单调增函数,
为单调增函数,
故![]() 不可能有两实根
不可能有两实根
∴a>0 令![]()
当![]() 递减,
递减,
∴![]() 处取到极大值
处取到极大值![]() ………………12分
………………12分
又当![]()
要使![]() 轴有两个交点当且仅当
轴有两个交点当且仅当![]() >0
>0
解得![]() ,故实数a的取值范围(0,
,故实数a的取值范围(0,![]() )
………………14分
)
………………14分
方法二:∵![]() 为偶函数,∴
为偶函数,∴![]() =0的根关于0对称.
=0的根关于0对称.
由![]() =0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根.
且两个正根和二个负根互为相反数
=0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根.
且两个正根和二个负根互为相反数
∴原命题可转化为:![]() 图像与x轴恰有两个不同的交点 …………6分
图像与x轴恰有两个不同的交点 …………6分
下面研究x>0时的情况
![]() 与直线
与直线![]() 交点的个数.
交点的个数.
∴当![]() 时,
时,![]() 递增与直线y=ax下降,
递增与直线y=ax下降,
故交点的个数为1,不合题意,∴a>0 ……………………………9分
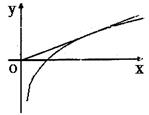 由几何意义知
由几何意义知![]() 与直线y=ax交点的个数为2时,直线y=ax的变化应是从x轴到与
与直线y=ax交点的个数为2时,直线y=ax的变化应是从x轴到与![]() 相切之间的情形.
…………………………………12分
相切之间的情形.
…………………………………12分
设切点![]()
∴切线方为
![]()
由切线与y=ax重合知![]()
故实数a的取值范围为(0,![]() )
………………………14分
)
………………………14分