专题考案(2)数列板块 第2课 数列的性质
(时间：90分钟 满分：100分)
题型示例
三个互不相等的实数成等差数列，如果适当排列这三个数，又可成为等比数列，这三个数的和为6，求这三个数.
分析 三个数适当排列，不同的排列方法有6种，但这里不必分成6种，因为若以三个数中哪一个数为等比中项，则只有三种情况，因此对于分类讨论问题，恰当的分类是解好问题的关键.
解 由已知，可设这三个数为a-d,a,a+d,则a-d+a+a+d=6,∴a=2,这三个数可表示为2-d,2,2+d,
(1)若2-d为等比中项，则有(2-d)2=2(2+d),解之得d=6或d=0(舍去).此时三个数为：-4,2,8.
(2)若2+d是等比中项，则有(2+d)2=2(2-d),解之得d=-6或d=0(舍去)，此时三个数为：8，2，-4.
(3)若2为等比中项，则22=(2+d)·(2-d),∴d=0(舍去).
综上可求得此三数为-4,2,8.
点评 此题给我们的启示是：数学解题既要精炼又要全面.
一、选择题 (8×3′＝24′)
1．下列各命题中，真命题是 ( )
A．若｛an｝成等差数列，则｛an｝也成等差数列
B．若｛an｝成等差数列，则｛an｝也成等差数列
C．若存在自然数n,使得2an+1=an+an+2，则｛an｝一定是等差数列
D．若｛an｝是等差数列，对任何自然数n都有2an+1=an+an+2
2．从{1,2,3,4,5,6,7,8,9,10}中任选3个不同的数使它们成等差数列，则这样的等差数列最多有 ( )
A.20个 B.40个 C.60个 D.80个
3．若正数a、b、c依次成公比大于1的等比数列，则当x>1时，logax、logbx、logcx( )
A.依次成等差数列 B.依次成等比数列
C.各项的倒数依次成等差数列 D.各项的倒数依次成等比数列
4．已知数列{an}，如果a1,a2-a1，a3-a2，…，an-an-1，…是首项为1，公比为
的等比数列，则an等于(n∈N)
（ ）
A.
B.
C.
D.
5．等差数列{an}的公差为
,S100=145,则a1+a3+a5+…+a99的值为
( )
A.60 B.85 C.
D.75
6．已知数列前n项和Sn=2n-1(n∈N*)，则此数列奇数项的前n项和为 ( )
A.
B.
C.
D.
7．正项等比数列｛an｝的首项a1=2-5，其前11项的几何平均数为25,若前11项中抽取一项后的几何平均数仍是25,则抽去一项的项数为 ( )
A.6 B.7 C.9 D.11
8．已知x、y为正实数，且x，a1,a2,y成等差数列，x,b1,b2,y成等比数列，则
的取值范围是 ( )
A.R B.(0,
C.［4,+
D.(-∞,0］∪［4,+∞)
二、填空题(4×3′＝12′)
9．等差数列｛an｝最初五项之和与其次五项之和的比为3∶4(n∈N*),则首项a1与公差d的比为 .
10．已知等比数列｛an｝的前n项和为Sn(n∈N)，若a3=3S2+2,a4=3S3+2,则公比q的值是 .
11．12-22+32-42+52-62+…+992-1002= .
12．若一个等差数列前3项的和为34,最后3项的和为146，且所有项的和为390,则这个数
列有 项.
三、解答题 (3×10′＋12′＋10′＝52′)
13．已知数列{an}的首项a1=a(a是常数且a≠-1),an=2an-1+1(n∈N*,n≥2).
(1){an}是否是等差数列？若是，求出{an}的通项公式；若不是，说明理由;
(2)设bn=an+c(n∈N*,c是常数)，若{bn}是等比数列，求实数c的值，并求出{bn}的通项公式.
14．设实数a≠0,且函数f(x)=a(x2+1)-(2x+
)有最小值-1.
(1)求a的值;
(2)设数列｛an｝的前n项和Sn=f(n),令bn=
,n=1，2,3…，证明数列｛bn｝是等差数列.
15．若数列｛an｝的前n项和Sn=-
(n∈N*)，求数列｛an｝的前n项和Tn.
16．在某两个正数之间插入一个数a,则三数成等差数列，若插入二个数b,c,则四数成等
比数列.
(1)求证:2a≥b+c;
(2)求证:(a+1)2≥(b+1)(c+1).
17．已知数列{an}的通项公式an=
(n∈N*)
(1)是否存在等于的项?为什么?
(2)此数列是否有相等的连续两项?若有，它们分别是哪两项;若没有，说明理由;
(3)此数列是否有值最小的项?为什么?
四、思考与讨论(12′)
18．在xOy平面上有点P1(a1,b1)，P2(a2,b2)，…，Pn(an,bn)，…，对每个自然数n，点Pn位于函数y=2000(
)x(0<a<10)的图象上，和点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形．
(1)求点Pn的纵坐标bn的表达式；
(2)若对每个自然数n，以bn、bn+1、bn+2为边长能构成一个三角形，求a的取值范围；
(3)设cn=lgbn(n∈N)．若a取(2)中确定的范围的最小整数，问数列{cn}前多少项的和最大?试说明理由．
参考答案
1．D A错，例如数列-3,-1,1，这样B也错，C应是对任意自然数n;D正是等差中项的性质.
2．B 由等差数列的概念知an-1+an+1=2an,所选的三个数只要首末两数之和为偶数，则该三数即可构成等差数列.因此，把所给的10个数分为 1,3,5,7,9;2,4,6,8,10两组,分别任取两数，另一数自然确定，共有2A
=5×4×2=40个.故选B.
3．C b2=ac
4．A an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=
=
．
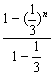5．A S100=(a1+a3+…+a99)+(a2+a4+…+a100)=145,又(a2+a4+…+a100)-(a1+a3+a5+…+a99)=50d
则
=a1+a3+a5+…+a99=60.
6．C an=2n-1，奇数项构成公比为4的等比数列.∴
.
7．A (a
·q1+2+…+10)
=25
q55=2110q=4.
抽取一项后，(a
·qx)
=25qx=2100x=50.
抽出的项的q的指数为5，故是第6项.
8．C 
9．13∶1 
a1∶d=13∶1.
|
②-①:a4-a3＝3（33－32）＝3a3，∴a4=4a3.
11．-5050 两项结合，利用平方差公式.
12．13 
，∵a1+an=a2+an-1=a3+an-2，
∴34+146=3(a1+an),a1+an=60．∴390=
·60，∴n=13.
13．解 （1）∵a1=a(a≠-1),a2=2a+1,a3=2a2+1=2(2a+1)+1=4a+3,
a1+a3=5a+3,2a2=4a+2.
∵a≠-1,∴5a+3≠4a+2,即a1+a3≠2a2,故{an}不是等差数列.
(2)由{bn}是等比数列，得b1b3=b
,即(a+c)(4a+3+c)=(2a+1+c)2,
化简得a-c-ac+1=0,即(a+1)(1-c)=0.
∵a≠-1,∴c=1,∴b1=a+1,q=
=2.
∴bn=b1qn-1=(a+1)·2n-1.
14．(1)解 ∵f(x)=a(x-)2+a-
有最小值-1.
∴a>0,且f()=a-=-1.∴a=1或a=-2(舍)，∴a=1.
(2)证明 由(1)知f(x)=x2-2x,∴Sn=n2-2n.
∴n=1时，a1=S1=-1；n≥2时，an=Sn-Sn-1=(n2-2n)-［(n-1)2-2(n-1)］=2n-3.
且a1=-1满足上式.∴an=2n-3,即｛an｝是首项为-1,公差为2的等差数列.
∴bn=
(a2+a4+…+a2n)=·
=·
=2n-1.
∴bn+1-bn＝［2(n+1)-1］-(2n-1)=2.∴｛bn｝是等差数列.
15．解 n≥2时，an=Sn-Sn-1=10-3n..
n=1时，a1=S1＝7满足上式，∴对n∈N*，an=10-3n.
令10-3n>0,则n<
,∴a1>0,a2>0，a3>0,a4<0，…
∴T（n）＝
.
|
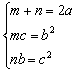
由①知a>0,由②，③知b,c>0,
∴
=m+n=2a2abc=b3+c3=(b+c)(b2+c2-bc)≥(b+c)(2bc-bc)=(b+c)bc,∴2a≥b+c.
(2)由①得a=
≥
=
a2≥bc
a2+2a≥bc+b+c(a+1)2≥bc+b+c+1=(b+1)(c+1).
17．解 (1)若数列中有等于的项，则有an=
n2-
n+
=,3n2-17n+20=0
解得n=4或n=
又n∈N则n=4,故数列的第4项等于.
(2)an=n2-n+,an+1=(n+1)2-(n+1)+.
若数列中有连续两项相等，则n2-n+=(n+1)2-(n+1)+解得n=
.
由于n∈N,故不存在相等的连续两项.
(3)an=(n-
)2+
,故当n=3时an取最小值.
点评 本题反映了数列的通项公式是关于项与它的序号的关系的式子，因此可运用方程思想，通过通项公式求出数列的各项或某一项所对应的项数.
另外，运用函数观点理解数列，其通项公式亦可视为定义域为正整数集的函数解析式，于是可运用有关函数知识解决一些数列问题.
18．解 (1)由题意，可知an=(n+n+1)=n+.
∴bn=2000()an=2000()
．
(2)∵函数y=2000()x在(-∞,+∞)上为减函数，∴对每个正整数n，有bn>bn+1>bn+2．
∴以bn、bn+1、bn+2为边能构成三角形的充要条件是bn+1+bn+2>bn，即+()2>1.
解得a<-5(1+
)或a>5(-1).
∵0<a<10,∴5(-1)<a<10,即为所求a的取值范围．
(3)易知a=7，则bn=2000(
).
于是cn=lgbn=3+lg2+(n+)lg0.7，且为递减数列．
由,解得n≤20.8 ∴n=20.
因此，{cn}的前20项和最大．