高考数学函数的最值测试

专题考案(1)函数板块 第4课  函数的最值

(时间：90分钟　满分：100分)

题型示例

求函数f(x)=(4-3a)x²-2x+a在区间［0,1］上的最大值.

解　先讨论二次项系数4-3a,分三种情况：

(1)当4-3a=0即a=时，原函数为f(x)=-2x+是减函数，在［0，1］上的最大值为f(0)==a；

(2)当4-3a>0,即a<时，抛物线开口向上，对称轴为x=>0;

①当对称轴位于区间［0,1］的中点，即=,a=时，最大值为f(0)=f(1)=2-2a;

②当对称轴位于区间［0,1］中点的左侧，即0<<,a<时，函数在［0,1］上的最大值为f(1)=2-2a;

③当对称轴位于区间［0,1］中点的右侧时，即>,<a<时，最大值为f(0)=a;

(3)当4-3a<0即a>时，抛物线开口向下，对称轴为x=<0,总在y轴左侧，所以函数在［0,1］上单调递减，最大值为f(0)=a.

综上所述，当a≤时，最大值为2-2a;当a>时，最大值为a.

点评　解决本题须根据需要逐层分类讨论，并将讨论的结果进行合并.

一、选择题(8×4′＝32′)

1．设实数x、y满足x+2y=1,x≤0，则x²+y²的最小值为　　　　　　　　　　　　 (　　)

A.　　　　 B.　　　　 C.　　　　 D.

2．已知x>0,y>0，且2x+5y=20，则lgx+lgy的最大值是　　　　　　　　　　　　 (　　)

A.0　　　　  B.1　　　　  C.2　　　　  D.5

3．设α、β是方程x²-2mx+3m-4=0的两实根，则(α-1)²+(β-1)²　　　　　　　　 ( 　 )

A.有最小值，无最大值　　　　B.有最大值，无最小值

C.既有最大值,又有最小值　　　D.既无最大值，又无最小值

4．函数f(x)=的最小值是　　　　　　　　　　　　　　  (　　)

A.　　　　B.3　　　　C.+　　　　D.3

5．若f(x),g(x)都是奇函数，且F(x)=f(x)+g(x)+2在(0,+∞)有最大值8，则在(-∞,0)上，F(x)有(　　)

A.最小值-8　　 B.最大值-8　　 C.最小值-6　　 D.最小值-4

6．如果0<a<1,0<x≤y<1,且(log_ax)·(log_ay)=1，那么xy　　　　　　　　　　　　 (　　)

A.没有最大值也没有最小值　　 B.没有最大值而有最小值

C.有最大值而没有最小值　　　 D.有最大值也有最小值

7．函数y=-x²-2ax(0≤x≤1)的最大值是a²，那么实数a的取值范围是　　　　　　 (　　)

A.0≤a≤1　　B.0≤a≤2　　C.-2≤a≤0　　D.-1≤a≤0

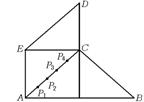
8．某县位于山区，农民居住区域大致呈右图所示的五边形，近似

由一个正方形和两个等腰直角三角形组成，若AB=60km,AE=CD=30km,

为了解决当地人们看电视难的问题，准备建一个电视转播台，理想方案

是转播台距五边形的顶点的距离的平方和最小，图中P₁、P₂、P₃、P₄是

AC的五等分点，则转播台应建在　　　　　　　　　　　　　  (　　)

A.P₁处　　　　B.P₂处　　　　C.P₃处　　　　D.P₄处

二、填空题 (4×4′＝16′)

9．若x²+y²-2y=0，则x²+4y的最大值是　　　　  .

10．x≥4,则函数y=x+的最小值为　　　　  .

11．某工厂生产某种产品的固定成本为200万元，并且每生产一单位产品，成本增加1万元，又知总收入R是单位产量Q的函数：R(Q)=4Q-Q²，则总利润L(Q)的最大值是　　万元，这时产品的生产数量为　　　　  (总利润＝总收入－总成本).

12．如果函数y=(x²-8x+17)的定义域为［2,5］,则该函数的最小值为　　　　.

三、解答题(4×10′＝40′)

13．证明：制作一个容积一定的圆柱形容器(有底有盖)以等边圆柱为用料最省.(不计加工损耗及接缝用料)

14．f(x)是定义在R上的奇函数，且满足如下两个条件:

①对于任意的x,y∈R,有f(x+y)=f(x)+f(y);

②当x>0时,f(x)<0,且f(1)=-2.

求函数f(x)在［-3,3］上的最大值和最小值.

15．已知定义域为［0,1］的函数f(x)同时满足：对于任意x∈［0,1］,总有f(x)≥0，f(1)=1;若x₁≥0,x₂≥0,x₁+x₂≤1,则有f(x₁+x₂)≥f(x₁)+f(x₂).

(1)求f(0)的值；

(2)求函数f()的最大值；

(3)证明：①当x∈(,1)时，有f(x)<2x成立；②当x∈［0,］时，有f(x)≤f(2x)成立.

16．如图所示，公园有一块边长为2a的等边△ABC的边角地，

现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，

E在AC上.

(1)设AD=x(x≥a),ED=y,求用x表示y的函数关系式.

(2)如果DE是灌溉水管，为节约成本，希望它最短，DE的位置应

该在哪里?如果DE是参观线路，则希望它最长，DE的位置又应该

在哪里?请予以证明.

四、思考与讨论(12′)

17．设f(x)是定义在R上以2为周期的函数，且是偶函数，在区间［2,3］上，f(x)=4-2(x-3)2．

(1)求x∈［1,2］时f(x)的表达式；

(2)若矩形ABCD的两个顶点A、B在x轴上，C、D在y=f(x)(0≤x≤2)的图象上，求矩形ABCD的面积S的最大值．

参考答案

1．D　x+2y=1(x≤0)表示射线，∴x²+y²的最小值为0²+()²=.

2．B　lgx+lgy=lg(xy)，又xy=(2x)·(5y)≤·=10，

∴lg(xy)≤1，即［lg(xy)］_max=1.

3．A　根据根与系数的关系建立关系式即得.

4．A　设M(x,0)是x轴上一点,A(0，2)，B(2,-1)，则=MA+MB,当M、A、B三点共线时，f(x)_min=.

5．D　F(x)-2=f(x)+g(x)是奇函数且在(0，+∞)上F(x)-2的最大值是8-2=6.于是F(x)-2在(-∞,0)上的最小值是-6,∴在(-∞,0)上，F(x)的最小值是-4.

6．C　∵0<a<1,0<x≤y<1,∴log_ax>0,∴log_ay>0，

log_ax+log_ay≥2=2，即log_a(xy)≥2,

∵0<a<1,∴0<xy≤a²,∴(xy)_max=a²，xy没有最小值.

7．D　y=-(x+a)²+a²，故0≤-a≤1,即-1≤a≤0.

8．D　设转播台建在AC上且与C相距xkm的P处，令AE=a，则AC=a,

依题意△ECD、△ABC均为等腰直角三角形，

∴PC²=x²,PA²=(a-x)²,PB²=(a)²+x²,PD²=a²+x²-2axcos135°,PE²=a²+x²-2axcos45°,

∴P到各顶点的距离的平方和

d²=PC²+PA²+PB²+PD²+PE²=5x²-2ax+6a²=5(x-)²+a².

∴当x=,即x=,P与P₄重合时，P到各顶点的距离的平方和d²最小，选D.

9．8　x²=2y-y²≥00≤y≤2,x²+4y=6y-y²=-(y-3)²+9，

∵0≤y≤2,∴当y=2时，(x²+4y)_max=8.

10．5　当x=4时,y_min=5.

11．250;300　L(Q)=4Q-Q²-(200+Q)=-(Q-300)²+250.

12．-2　y=(x²-8x+17)= ［(x-4)²+1］.令y=u,u=(x-4)²+1(5≥u≥1),

又y=u在［1,5］上为减函数，要求函数y=u的最小值.可转化为求u=(x-4)²+1的最大值，所以当u=5时，y_min=-2.

13．证明　设圆柱的高为h，底面半径为r,容积为V，则πr²h=V,即r²h=.

S_全=2πr²+2πrh=2π(r²++)≥2π·=6π·，

当且仅当r²=,r=，即此圆柱为等边圆柱时，用料最省.

14．解　设0≤x₁≤x₂≤3,则由条件①得f(x₂)=f［(x₂-x₁)+x₁］=f(x₂-x₁)+f(x₁)

即f(x₂-x₁)=f(x₂)-f(x₁)，∵x₂>x₁,∴x₂-x₁>0由条件②得:f(x₂-x₁)<0，

∴f(x₂)-f(x₁)<0即f(x₁)>f(x₂)，∴f(x)在［0,3］上是减函数.

又f(x)为奇函数,∴f(x)在［-3,0］上也是减函数.

从而f(x)在［-3,3］上是减函数,

∴f(x)_max=f(-3)=-f(3)=-f(1+2)=-f(1)-f(1+1)=-3f(1)=6f(x)_min=f(3)=-f(-3)=-6.

点评　对于抽象函数，往往是通过研究函数的单调性求最值.

15．(1)解　令x₁=x₂=0,由条件得f(0+0)≥f(0)+f(0),∴f(0)≤0.又知f(0)≥0,∴f(0)=0.

(2)解　任取0≤x₁<x₂≤1.∴x₂-x₁∈(0,,

∴f(x₂)-f(x₁)=f［(x₂-x₁)+x₁］-f(x₁)≥f(x₂-x₁)+f(x₁)-f(x₁)≥0,∴f(x₂)≥f(x₁).

于是当0≤x≤1时，有f(x)≤f(1)=1,即函数f(x)的最大值为1.

(3)证明　①∵<x≤1,∴2≥2x>1.又f(x)≤1,∴当x∈(,1)时，f(x)<2x.

②当x∈［0,］时，0≤2x≤1,∴f(2x)≥f(x)+f(x)=2f(x),∴f(x)≤f(2x).

16．解　(1)△ABC的边长为2a,D在AB上，则a≤x≤2a,

∵S△ADE=S_△ABC，∴x·AEsin60°=··(2a)².

∴AE=，在△ADE中，由余弦定理y²=x²+-2x·cos60°，

∴y²=x²+-2a²，∴y=(a≤x≤2a).

(2) y=(a≤x≤2a).

令x²=t，则a²≤t≤4a²,且y=.

设f(t)=t+ ，当t∈［a²,2a²］时，可证f(t)为减函数.

当t∈［2a²,4a²］时，可证f(t)为增函数.

又f(2a²)=4a²,f(4a²)=f(a²)=5a²，∴t=2a²时f(t)有最小值，

即x=a时，y_min=a.此时DE∥BC;

t=a²或4a²时，f(x)有最大值，即x=a或x=2a时，y_max=a，此时DE为AB或AC边上的中线.

17．解　(1)当1≤x≤2时，-3≤x-4≤-2，2≤4-x≤3.

∴f(x)=f(x-4)=f(4-x)=4-2(4-x-3)²=4-2(x-1)²．

(2)当0≤x≤1时，2≤x+2≤3，∴f(x)=f(x+2)=4-2(x-1)²．

∴0≤x≤2时，f(x)=4-2(x-1)²．

设A(1-t,0),B(1+t,0)(0≤t≤1).

∴BC=AD=f(1+t)=4-2t²．

S=AB·BC=2t(4-2t²)=4t(2-t²).

∴S²=16t²(2-t²)²≤8·=8×()³．

∴S≤,等号成立时t=.∴S_max=.