高考文科数学第一次统一测试试题
本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,答题时间120分钟。
第Ⅰ卷(选择题,共50分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确的选项填在答题卡的表格里(每小题5分,共50分).
1.下列各组两个集合![]() 和
和![]() ,表示同一集合的是( )
,表示同一集合的是( )
A.![]() =
=![]() ,
,![]() =
=![]() B.
B.![]() =
=![]() ,
,![]() =
=![]()
C.![]() =
=![]() ,
,![]() =
=![]() D.
D.![]() =
=![]() ,
,![]() =
=![]()
2.设![]() ,则满足
,则满足![]() 的集合
的集合![]() 的个数为( )
的个数为( )
A.8 B.7 C.4 D.1
3.与函数![]() 是同一函数的是 ( )
是同一函数的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.
4.下列函数在区间![]() 上为增函数的是( )
上为增函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设![]() ,
,![]() ,
,![]() 则
则![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
6.方程log2(x+4)=3x实根的个数是( )
A.0 B.1 C.2 D.3
7.当![]() 时,函数
时,函数![]() 和
和![]() 的图象只可能是( )
的图象只可能是( )

8.若函数![]() 的值域是
的值域是![]() ,则其定义域是( )
,则其定义域是( )
A. ![]() B.
B.![]()
C. ![]() D.
D.![]()
9.函数![]() 在闭区间
在闭区间![]() 上有最大值3,最小值2,则
上有最大值3,最小值2,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.一水池有2个相同进水口,1 个出水口,每个进、出水口进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.
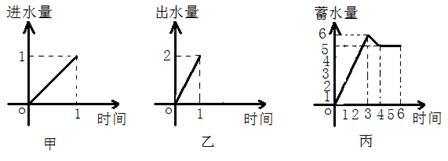 |
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水,则一定正确的论断是( )
A.① B.①② C.①③ D.①②③
第Ⅱ卷(非选择题,共100分)
二、填空题:请把答案填在答题卡中的横线上(每小题5分,共20分).
11.计算:![]() ,
,![]() ;
;
12.已知集合![]() 等于
;
等于
;
 13.已知定义在区间
13.已知定义在区间![]() 上的函数
上的函数![]() ,图象如右图所示,
,图象如右图所示,
对满足![]() 的任意
的任意![]() 、
、![]() ,给出下列结论:
,给出下列结论:
①![]() ;
;
②![]() ;
;
③![]() .
.
其中正确的结论的序号是______ __(把所有正确结论的序号都填上);
14.已知函数![]() 是定义域为R的奇函数,且方程
是定义域为R的奇函数,且方程![]() 在
在![]() 内的解集A只含一个元素,则方程
内的解集A只含一个元素,则方程![]() 在R内的解集B的子集个数是
.
在R内的解集B的子集个数是
.
三、解答题:解答应写出文字说明、证明过程或演算步骤(共80分).
15.已知R为全集,![]() 求
求![]() .
.
16.已知定义域在R上的函数![]() ,对任意的
,对任意的![]() 均有:
均有:![]() ,且
,且![]() .
.
(1)求![]() 的值;(2)判断
的值;(2)判断![]() 的奇偶性.
的奇偶性.
17.已知函数![]() .
.
(1)求![]() 的定义域;(2)证明:函数
的定义域;(2)证明:函数![]() 在定义域内单调递增.
在定义域内单调递增.
18.已知函数![]() 为奇函数.
为奇函数.
(1)求![]() 的值; (2)求函数
的值; (2)求函数![]() 的值域; (3)比较
的值域; (3)比较![]() 与
与![]() 的大小。
的大小。
19.设函数![]() .
.
(1)作出![]() 的大致图象;
的大致图象;
(2)证明: 当![]() ,且
,且![]() 时,
时,![]() .
.
20.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元。
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
(2)设一次订购量为![]() 个,零件的实际出厂单价为P元,写出函数
个,零件的实际出厂单价为P元,写出函数![]() 的表达式;
的表达式;
(3)已知销售商以80元的单价出售该零件,若一次订购![]() 个零件,则每个零件所需的销售成本为
个零件,则每个零件所需的销售成本为![]() 元,求销售商售出每个零件所获利润的最大值。(销售商售出一个零件的利润=出售单价-实际出厂单价-销售成本)
元,求销售商售出每个零件所获利润的最大值。(销售商售出一个零件的利润=出售单价-实际出厂单价-销售成本)
参考答案
一、 选择题:(每小题5分,共50分)。
| 题目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | D | D | B | C | B | B | D | A |
二、 填空题:(每小题5分,共20分)。
11、0(3分),
2(2分) 12、![]() 13、 ② ③ 14、8
13、 ② ③ 14、8
三、 解答题:(共80分)
15. 解:由![]() ,得
,得![]() ,
,
解之得![]() .……………………………………………………………………4分
.……………………………………………………………………4分
![]() . ………………………………………………………6分
. ………………………………………………………6分
由![]() ,得
,得![]() ,
,
即![]() ,解之得
,解之得![]() ……………………………………………………10分
……………………………………………………10分
故![]() =
=![]() .…………………………………………………………12分
.…………………………………………………………12分
16.解:(1)令![]() ,则有
,则有![]() ,
,
因为![]() ,
,
所以![]() .…………………………………………………………………4分
.…………………………………………………………………4分
(2)令![]() ,则有
,则有![]() ,由
,由![]() ,
,
所以![]() ,
,
即有:![]() ,
,
所以![]() 是偶函数.……………………………………………………………12分
是偶函数.……………………………………………………………12分
17.解:(1)由![]() ,解得
,解得![]() ∴
∴![]() 的定义域为
的定义域为![]() ……………………4分
……………………4分
(2)证明:设![]() ,
,
∴![]()
则![]() ,因此:
,因此:![]() ,
,
即:![]() ,则
,则![]() 在(-
在(-![]() ,0)上为增函数。…………………14分
,0)上为增函数。…………………14分
18.解:(1)定义域为![]() ,
,
由![]() 为奇函数知,对于
为奇函数知,对于![]() 都有:
都有:![]()
即:![]()
![]()
![]()
![]() ∴
∴ ![]()
![]()
![]()
∴![]() ,因此:
,因此: ![]() …………………………………………………………5分
…………………………………………………………5分
(2)由![]() 得:
得:![]()
∴![]()
![]()
∴![]() 或
或![]()
即:值域为![]() ……………………………………………………10分
……………………………………………………10分
(3)∵![]()
∴![]() 在
在![]() 上为减函数, 又
上为减函数, 又 ![]()
因此:![]() ………………………………………………………………14分
………………………………………………………………14分
 19.解:(1)由
19.解:(1)由![]() 可得:,
可得:,

当![]() 时,
时,![]() 可以看成
可以看成![]() 向上平移一个单位得到的;
向上平移一个单位得到的;
当![]() 时,
时,![]() 可以看成
可以看成![]() 向下平移一个单位得到的,如上图所示.……7分
向下平移一个单位得到的,如上图所示.……7分
(2)由![]() ,
,![]() ,
,
因为![]() 故
故![]() ,即:
,即:![]() ,
,
又∴![]() ,
,
所以![]() ,即
,即![]() ,
,![]() 由于
由于![]() ,所以
,所以![]() .………………14分
.………………14分
20. 解:(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为![]() 个,
个,
则 ![]()
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元。………3分
(2)设一次订购![]() 个零件,则
个零件,则
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以 ……………………8分
……………………8分
(3)设销售商一次订购![]() 个零件时,每个零件获得的利润为
个零件时,每个零件获得的利润为![]() 元,则
元,则
 (
(![]() )
)
即: (
(![]() )
)
当![]() 时
时 ![]()
当![]() 时
时 ![]()
当![]() 时
时 ![]()
因此,当一次订购500个时销售商的利润最大,最大利润为23元。………………14分