圆锥曲线(三) ----(圆锥曲线的综合问题)
【考点透视】
解析几何是联系初等数学与高等数学的纽带，它本身侧重于形象思维、推理运算和数形结合，综合了代数、三角、几何、向量等知识
反映在解题上，就是根据曲线的几何特征准确地转换为代数形式，根据方程画出图形，研究几何性质学习时应熟练掌握函数与方程的思想、数形结合的思想、参数的思想、分类与转化的思想等，以达到优化解题的目的
具体来说，有以下三方面：
（1）确定曲线方程，实质是求某几何量的值；含参数系数的曲线方程或变化运动中的圆锥曲线的主要问题是定值、最值、最值范围问题，这些问题的求解都离不开函数、方程、不等式的解题思想方法有时题设设计的非常隐蔽，这就要求认真审题，挖掘题目的隐含条件作为解题突破口
（2）解析几何也可以与数学其他知识相联系，这种综合一般比较直观，在解题时保持思维的灵活性和多面性，能够顺利进行转化，即从一知识转化为另一知识
（3）解析几何与其他学科或实际问题的综合，主要体现在用解析几何知识去解有关知识，具体地说就是通过建立坐标系，建立所研究曲线的方程，并通过方程求解来回答实际问题在这一类问题中“实际量”与“数学量”的转化是易出错的地方，这是因为在坐标系中的量是“数量”，不仅有大小还有符号
【适应性训练】
1.设
，“
”是“曲线
为椭圆”的
（ ）
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
2.到两定点
距离之和为
的点的轨迹是
（ ）
A.椭圆 B.AB所在直线 C.线段AB D.无轨迹
3.若点
在椭圆
上，则
的最小值为
（ ）
A.1 B.－1
C.－
D.以上都不对
4.以正方形
的相对顶点
为焦点的椭圆，恰好过正方形四边的中点，则该椭圆的离心率为
（ ）
A.
B.
C.
D.
5.已知
是椭圆
+
＝1的两个焦点，
是椭圆上的点，当
时，
的面积最大，则有
（ ）
A.m=12，n=3 B.m=24，n=6 C.m=6，n=
D.m=12，n=6
6.设
，
是双曲线
上位于第一象限的点，对于命题①
；②以线段
为直径的圆与圆
相切；③存在常数
，使得到直线
的距离等于
.其中所有正确命题的序号是________.
【典型例题选讲】
例1.如图，O为坐标原点，直线l在x轴和y轴上的截距分别是a和b（a>0，b≠0），且交抛物线y2=2px（p>0）于M（x1，y1），N（x2，y2）两点
（1）写出直线l的截距式方程；
（2）证明：
+
=
；（3）当a=2p时，求∠MON的大小
例2.已知椭圆C的方程为
+
=1（a>b>0），双曲线－=1的两条渐近线为l1、l2 ，过椭圆C的右焦点F作直线l，使l⊥l1，又l与l2交于P点，设l与椭圆C的两个交点由上至下依次为A、B .（如图）
（1）当l1与l2夹角为60°，双曲线的焦距为4时，求椭圆C的方程；
（2）当
时，求
的最大值
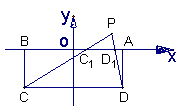
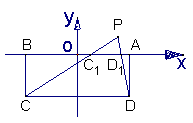
例3.如图, 矩形ABCD中, 
, 以AB边所在的直线为x轴, AB的中点为原点建立直角坐标系, P是x轴上方一点, 使PC、PD与线段AB分别交于
、
两点, 且
成等比数列, 求动点P的轨迹方程
例4.抛物线y2=4px（p>0）的准线交x轴于M点，过点M作直线l交抛物线于A、B两点.
（1）若线段AB的垂直平分线交x轴于N（x0，0），求证：x0>3p；
（2）若直线l的斜率依次为p，p2，p3，…，线段AB的垂直平分线与x轴的交点依次为N1，N2，N3，…，当0<p<1时，求
+
+…+
的值.
BCCDA 6、①②③
例1：（1）解：直线l的截距式方程为
+
=1
（2）证明：由+=1及y2=2px消去x可得by2+2pay－2pab=0
点M、N的纵坐标为y1、y2，
故y1+y2=
，y1y2=－2pa
所以+=
=
=
（3）解：设直线OM、ON的斜率分别为k1、k2，
则k1=
，k2=
当a=2p时，由（2）知，y1y2=－2pa=－4p2，
由y12=2px1，y22=2px2，相乘得（y1y2）2=4p2x1x2，
x1x2=
=
=4p2，
因此k1k2=
=
=－1
所以OM⊥ON，即∠MON=90°
例2：解：（1）∵双曲线的渐近线为y=±
x，两渐近线夹角为60°，
又<1，∴∠POx=30°，即=tan30°=
∴a=b
又a2+b2=4，
∴a2=3，b2=1
故椭圆C的方程为
+y2=1
（2）由已知l：y=
（x－c），与y=x解得P（
，
），
由
=λ
得A（
，
）
将A点坐标代入椭圆方程得
（c2+λa2）2+λ2a4=（1+λ）2a2c2
∴（e2+λ）2+λ2=e2（1+λ）2
∴λ2=
=－［（2－e2）+
］+3≤3－2
∴λ的最大值为－1
例3：解:
显然有
,
设
,
三点共线, 
,
, 又
三点共线,
, 
, 
,
, 
,
化简得动点P的轨迹方程为
例4：（1）证明：设直线l方程为y=k（x+p），代入y2=4px.
得k2x2+（2k2p－4p）x+k2p2=0.
Δ=4（k2p－2p）2－4k2·k2p2>0，
得0<k2<1.
令A（x1，y1）、B（x2，y2），则x1+x2=－
，y1+y2=k（x1+x2+2p）=
，
AB中点坐标为（
，
）.
AB垂直平分线为y－=－
（x－）.
令y=0，得x0=
=p+
.
由上可知0<k2<1，∴x0>p+2p=3p.
∴x0>3p.
（2）解：∵l的斜率依次为p，p2，p3，…时，AB中垂线与x轴交点依次为N1，N2，N3，…（0<p<1）.
∴点Nn的坐标为（p+
，0）.
NnNn+1=（p+）－（p+
）=
，
=
，
所求的值为
［p3+p4+…+p21］=
.