专题十五 圆锥曲线综合问题
1.
已知向量![]() ,
,![]() ,
,![]() (其中
(其中![]() ,
,![]() 是实数),又设向量
是实数),又设向量![]() ,
,![]() ,且
,且![]() ,点
,点![]() 的轨迹为曲线C.
的轨迹为曲线C.
⑴ 求曲线![]() 的方程;
的方程;
⑵ 设曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,过点
,过点![]() 作一条直线
作一条直线![]() 与曲线
与曲线![]() 交于另一点
交于另一点![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
2.
如图所示,已知点![]() ,
,![]() 、
、![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,并且满足
轴上运动,并且满足![]() ,
,![]() .
.
⑴ 求动点![]() 的轨迹方程;
的轨迹方程;
⑵ 设过点![]() 的直线与
的直线与![]() 的轨迹交于
的轨迹交于![]() 、
、![]() 两点,设
两点,设![]() ,求直线
,求直线![]() 、
、![]() 的斜率之和.
的斜率之和.
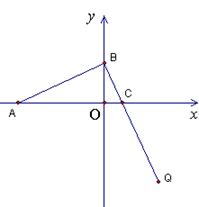
3.
已知![]() 、
、![]() ,点
,点![]() 、点
、点![]() 满足
满足![]() ,
,![]() ,
,
⑴ 求点![]() 的轨迹方程;
的轨迹方程;
⑵ 过点![]() 作直线
作直线![]() 交以
交以![]() 、
、![]() 为焦点的椭圆于
为焦点的椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点到
的中点到![]() 轴的距离为
轴的距离为![]() ,且直线
,且直线![]() 与点
与点![]() 的轨迹相切,求该椭圆的方程.
的轨迹相切,求该椭圆的方程.
4.
椭圆![]()
![]() 的焦点在
的焦点在![]() 轴上,其右顶点关于直线
轴上,其右顶点关于直线![]() 的对称点在椭圆的左准线上.
的对称点在椭圆的左准线上.
⑴ 求椭圆的方程;
⑵ 过椭圆左焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,交椭圆左准线于点
两点,交椭圆左准线于点![]() .设
.设![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 的面积.
的面积.
5.
已知![]() 为坐标原点,点
为坐标原点,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,点
,点![]() 、
、![]() 、
、![]() 运动时满足
运动时满足![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
⑵ 设![]() 、
、![]() 是
是![]() 上两点,若
上两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
6.
双曲线![]()
![]() 的离心率为
的离心率为![]() ,
,![]() 、
、![]() 分别是双曲线的左顶点、右焦点,过点
分别是双曲线的左顶点、右焦点,过点![]() 的直线
的直线![]() 交双曲线的右支于
交双曲线的右支于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,
点,![]() 、
、![]() 分别交右准线于
分别交右准线于![]() 、
、![]() 两点.
两点.
⑴ 若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
⑵ 证明:![]() 、
、![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
1.
⑴由已知,![]()
![]()
![]()
即所求曲线的方程是:![]()
⑵由(I)求得点M(0,1),显然直线l与x轴不垂直,
故可设直线l的方程为y=kx+1.
由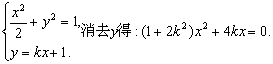
解得x1=0, x2=![]() 分别为M,N的横坐标).
分别为M,N的横坐标).
由![]()
所以直线l的方程x-y+1=0或x+y-1=0.
2.
⑴ ![]() ……2分
……2分
![]()
由已知![]() ……………………4分
……………………4分
![]() …………5分
…………5分
⑵ 设过点A的直线为![]() 、F(x2,y2)
、F(x2,y2)
联立方程组![]() ……7分
……7分
y1y2=12p2………………8分
![]() …………10分
…………10分
![]() , 所以
, 所以
 …………………………13分
…………………………13分
由y1y2=12p2,得![]() =0…………14分
=0…………14分
3.
⑴ 设![]() 、
、![]() 点的坐标分别为
点的坐标分别为![]() ,
,![]() ,则:
,则:
![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
 ,解得
,解得
![]()
![]() ,即
,即![]()
![]()
![]() ,即为点
,即为点![]() 的轨迹方程
的轨迹方程
⑵ 易知直线![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() 的方程为
的方程为![]() ①.
①.
又设椭圆方程为![]()
![]() ②.
②.
因为直线![]() 与圆
与圆![]() 相切,故
相切,故![]() ,解得
,解得![]()
将①代入②整理得,![]() ,
,
而![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
由题意有![]()
![]() ,求得
,求得![]() ,经检验,此时
,经检验,此时![]()
故所求的椭圆方程为![]()
4.
⑴ 椭圆的右顶点为![]() (2,0),
(2,0),
设![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
则 ,解得
,解得![]() ,
,
![]()
![]() ,
,![]()
![]()
![]() ,所求椭圆方程为
,所求椭圆方程为![]()
⑵ 设A![]()
由
所以![]() ………① ,
………① ,![]() ………②
………②
因为![]() ,即
,即![]() ,
,
所以![]() ……③
……③
由①③得![]()
代入②得,![]() ,整理得
,整理得![]()
所以![]() 所以
所以![]()
由于对称性,只需求![]() 时,△OAB的面积.
时,△OAB的面积.
此时,![]() 所以
所以![]()
5.
⑴ ![]()
![]()
![]()
![]() 为AF的中点.
为AF的中点.
![]()
![]()
![]()
![]()
![]()
![]() 是
是![]() 的垂直平分线
的垂直平分线 ![]()
![]()
![]()
![]()
![]() A、E、P三点共线
A、E、P三点共线
![]() P为AF的垂直平分线与AE的交点
P为AF的垂直平分线与AE的交点
![]()
![]()
∴ 点P的轨迹为椭圆,且![]() ,
,![]()
![]()
![]() ,
,![]()
∴ 所求的椭圆方程为![]()
⑵ 设两交点的坐标为![]() 、
、![]() 则
则
![]() ,
,![]()
由已知![]() 可得:
可得:
![]() ,
,![]()
由上式可组成方程组为
把⑶、⑷代入⑴得![]() ⑸
⑸
⑸ — ⑵×4得![]() ,把
,把![]() 代入⑵得
代入⑵得![]()
直线MN与x轴显然不垂直,
∴ 所求直线MN的斜率![]()
∴ 所求的直线MN的方程为![]()
6.
⑴ 解:设![]() ,
,![]() ,因为双曲线的离心率为
,因为双曲线的离心率为![]() ,
,
所以![]() ,
,![]() ,双曲线方程为
,双曲线方程为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为直线![]() ,所以
,所以![]() ,
,
点Q是双曲线上一点,所以![]() ,
,
整理得,![]() ,解得
,解得![]()
⑵ 证明:设![]() ,
,![]()
由已知![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
由 ,得
,得![]()
所以![]() ,
,![]() ,
,
![]()
![]()
所以,![]()