正弦、余弦的诱导公式;任意角的三角函数习题课
一. 教学内容
正弦、余弦的诱导公式;任意角的三角函数习题课
二. 教学重、难点
重点:运用诱导公式,把求任意角的三角函数值问题转化为求0°~90°间角的三角函数值的问题,任意角的三角函数。
难点:对诱导公式中符号的确定
【典型例题】
[例1] 设![]() ,求
,求 的值。
的值。
解:
方法一:
∵ ![]()
∴ 原式
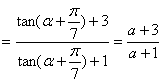
方法二:
原式


[例2] 设 求
求![]() 的值。
的值。
解:![]()
∵ ![]() ∴
∴ ![]() ∴
∴ ![]()
[例3] 已知![]() ,求
,求![]() 的值。
的值。
解:∵ ![]() ∴
∴ ![]()
又![]()
∴ 原式![]()
![]()
![]()
[例4] 已知![]() ,
,![]() 为第三象限角,求
为第三象限角,求![]() 的值。
的值。
解:![]() 又 ∵
又 ∵ ![]() 是第三象限角,
是第三象限角,![]()
∴ ![]()
![]() ∴
∴ ![]()
∵ ![]()
∴ 原式![]()
[例5] 已知![]() ,
,![]() 是关于x的方程
是关于x的方程![]() 的两实根,且
的两实根,且![]() ,求
,求![]() 的值。
的值。
解:∵ ![]() ,
,![]() 是方程
是方程![]() 的两实根
的两实根
∴ ![]() ∴
∴ ![]()
∵ ![]() ∴
∴ ![]() ,
,![]() ,
,![]() ,
,![]()
∴ ![]() ∴
∴ ![]() ∴ 方程化为
∴ 方程化为![]()
∴ ![]() 即
即![]() ∴
∴ ![]()
∴ ![]() ,
,![]()
∴ ![]()
[例6] 已知![]() ,求
,求![]() 的值。
的值。
解:由已知等式变形可得![]()
即![]() ∴
∴ ![]()
∴ ![]() ∴
∴ ![]()
[例7] 已知:![]() ,求
,求![]() 和
和![]() 的值。
的值。
解:由![]() 平方,可得
平方,可得![]()
∴ ![]()
![]()
![]()
[例8] 已知![]() ,求证:
,求证:![]()
证:由已知![]()
![]()
![]()
∴ ![]()
【模拟试题】
一. 选择
1. ![]() 的值等于( )
的值等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 若![]() 则
则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 已知扇形的面积是![]() ,半径是1,则扇形的中心角是( )
,半径是1,则扇形的中心角是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 若![]() ,
,![]() 则
则![]() 等于( )
等于( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
二. 填空题
1. 计算![]()
2. 化简![]() (
(![]() )=
)=
3. 已知![]() ,
,![]() 且
且![]() 是象限角,则实数
是象限角,则实数![]() ,
,![]() 是第 象限角。
是第 象限角。
4. 若![]() 为第一象限角,则在
为第一象限角,则在![]() ,
,![]() ,
,![]() ,
,![]() 中必定取正值的是 。
中必定取正值的是 。
三. 解答题
1. 已知![]() 求
求![]() 的值。
的值。
2. 求函数![]() 的最大值和最小值。
的最大值和最小值。
3. 已知![]() ,
,![]() 求
求![]() 的值。
的值。
【试题答案】
一.
1. A 2. A 3. C 4. C
二.
1.
![]() 2.
2.  3.
3. ![]() ,I 4.
,I 4. ![]()
三.
1.
解:∵ ![]()
∴ ![]()
∴ 原式![]()
2.
解:![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
3.
解:∵ ![]() ∴
∴ ![]()
∴ ![]()