专题考案(1)函数板块 测试
第Ⅰ卷 (选择题 共60分)
一、选择题(12×5′＝60′)
1.下列四个函数中，在区间(0,1)上为增函数的是 ( )
A.y=
B.y=sinx C.y=
D.y=
2.已知f (x)＝
的定义域为(0，1)，则f (x)有 ( )
A.最小值2+2
B.最大值2-2
C.最小值2-2
D.最大值2+2
3.要使函数y=
在［1,2］上存在反函数，则a的取值范围是 ( )
A.a≤1 B.a≥2 C.a≤1或a≥2 D.1≤a≤2
4.二次函数f (x)满足f (x+2)=f (2-x),且f (a)≤f (0)≤f (1),则实数a的取值范围是 ( )
A.a≥0 B.a≤0 C.0≤a≤4 D.a≤0或a≥4
5.已知g(x)=1-2x,f［g (x)］=
(x≠0),则
等于 ( )
A.15 B.1 C.3 D.30
6.对于任意a∈［-1,1］,函数f (x)=
的值总大于0,则x的取值范围是 ( )
A.{x1<x<3} B.{xx<1或x>3} C.{x1<x<2} D.{xx<1或x>2}
7.设f (x)的定义域为R，且f (-x)=-f (x)，f (x+d)<f (x)(d>0)，当不等式f (a)+f (
)<0成立时，a的取值范围是 ( )
A.(-∞，-1)∪(0，+∞) B.(-1，0)
C.(-∞，0)∪(1，+∞) D.(-∞，1)∪(1，+∞)
8.已知x,y∈R，且
，则x与y一定满足 ( )
A.x+y≥0 B.x+y≤0 C.x-y≥0 D.x-y≤0
9.已知函数f (x)≠-1，且对定义域内任意x总有关系［f (x+π)+1］［f (x)+1］=2，那么下列结论中一定正确的是 ( )
A.f (x)不一定有周期性 B.f (x)是周期为π的函数
C.f (x)是周期为2π的函数
D.f (x)是周期为
的函数
10.在区间［
，2］上，函数f (x)=
与g(x)=2x+
在同一点取得相同的最小值，那么f (x)在［，2］上的最大值是 ( )
A.
B.4
C.8
D.
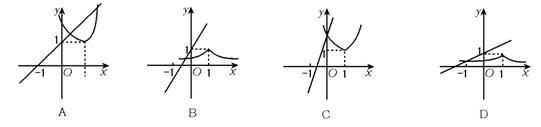
11.已知函数f(x)=
(a>0且a≠1)，在同一直角坐标系中，y=
与y=
的图象可能是( )
|
12.已知函数f (x)=
，g(x)=
，构造函数F(x)定义如下：当F(x)≥g(x)时，F(x)＝f(x)；当f (x)<g(x)时，F(x)＝-g(x),那么F(x) ( )
A.有最大值1，无最小值 B.有最小值0，无最大值
C.有最小值-1，无最大值 D.无最小值，也无最大值
第Ⅱ卷 (非选择题 共90分)
二、填空题(4×4′=16′)
13.若f (x)=x-2a+x-1函数值恒为正,则a的取值范围是 .
14.f (x)与g(x)分别是一个奇函数和一个偶函数，若f (x)-g(x)=,则f (-1)、g(0)、g(-2)从小到大的顺序是
.
15.记号［x］表示不超过4的最大整数，则y＝［x］的图象与直线y＝x-1的图象的交点个数是 .
16.设函数f(x)的反函数为h(x)，函数g(x)的反函数为h(x+1)，已知f (2)=5,f (5)=-2，f (-2)=8，那么g(2)、g(5)、g(8)、g(-2)中，一定能求出具体数值的是 .
三、解答题(5×12′+14′＝74′)
17.已知函数f (x)=lg(kx),g(x)=lg(x+1).
(1)求f (x)-g(x)的定义域；
(2)若方程f (x)=g (x)有且仅有一个实根，求实数k的取值范围.
18.对于映射f (x)＝
，有适合f (x)＝x的x时，这个x叫做f (x)的不动点.
(1)求使f (x)有绝对值相等且符号相反的两个不动点时a、b所满足的条件.
(2)在(1)的条件下，当a=3时，f (x)的两个不动点对应于函数y=f (x)图象上的两个点，记为A、B，C为函数y=f
(x)图象上另一点，且
>2，求点C到直线AB距离的最小值及取得最小值时对应的C点的坐标.
19.已知函数f (x)=
(a>0，x>0).
(1)求证：f (x)在(0，+∞)上是递增函数.
(2)若f (x)在［m,n］上的值域是［m,n］(m≠n)，求a的取值范围并求相应的m、n的值.
(3)若f (x)≤2x在(0，+∞)上恒成立，求a的取值范围.
20.西部某地区因交通问题严重制约经济发展，某种土特产品只能在本地销售，每年投资x万元，所获利润为p=-
(万元).在实施西部大开发战略中，该地区在制订经济发展十年规划时，拟开发此种土特产品.开发前后，财政预算每年均可投入专项资金60万元，要开发此产品，需先用5年时间修通公路，所需资金从60万元的预算资金中每年拿出30万元.公路修通后该土特产品在异地销售，每投资x万元，可获利润：q=-
(万元). 问从10年的总利润
来看，该项目有无开发价值?
21.已知二次函数
(a、b∈R,a>0),设方程f (x)=x的两个实数根为
和
.
(1)如果<2<<4,设函数f (x)的对称轴为x=
,求证：>-1;
(2)如果<2,-=2,求b的取值范围.
22.设二次函数 (a>0且b≠0).
(1)已知f (0)=f (1)＝f (-1)=1，求f(x)的解析式和f(x)的最小值.
(2)已知f (x)的对称轴方程是x=1，当f (x)的图象在x轴上截得的弦长不小于2时，试求a、b、c满足的条件.
(3)已知b≤a，f (0)≤1，f (1)≤1，f (-1)≤1.证明：当x≤1时，f (x)≤.
函数测试参考答案
1.B
2.Ｂ f (x)=
，由x∈(0，1)知，
，
则
，
故f (x)≤2-2，当且仅当
，
即
，此时x∈(0，1)取“＝”.
3.C 要使
在［1，2］上存在反函数，则函数在区间［1，2］上为单调函数，即区间［1，2］为函数单调区间的子区间，函数的单调区间为(-∞，a
，
a,+∞)，故a≤1或a≥2.
4.D 由f (x+2)=f (2-x)知x=2为对称轴,∴f (a)=f (4-a)又开口向下∴a≤0或a≥4,故选D.
5.A 由g(x)=得x=
,∴
.
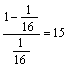6.B 设g(a)=(x-2)a+
(x≠2),则g(a)为关于a的一次函数，因此g(a)在a∈［-1,1］恒大于零的充要条件为
x<1或x>3.
7.A 由f (-x)=-f (x)知函数y=f (x)为奇函数；由f (x+d)<f (x)(d>0)知y=f (x)为减函数.
故f (a)+f
()<0
f (a)<f (-)a>-
，故a<-1或a>0.
8.A 不等式即
,函数
为关于t的增函数.∴x≥-y,即x+y≥0.
9.C f (x+π)＝
.由此可得f［(x+π)+π］＝
，
代入f (x+π)＝
，化简得f (x+2π)＝f(x).
10.B g(x)=x+x+≥
，当且仅当x=，即x=1∈［,2］时取“＝”号.
依题意，f(x)=
.x∈［，2］时，
.
11.D 由题得y=
(a>0且a≠1),由a≠1可排除选项A；令x=0,则y=1,可排除选项C;对于选项B、D，
的图象无多大区别，关键在于
的图象，分析后可看出B选项a>1,D选项0<a<1,故需由
来判定a的范围，比较明显，令t=x-1,则
(t>0)为减函数，即可知0<a<1,故选D.
|
最小值-1，无最大值.
13.a＞ 利用数形结合思想可知2a>1,∴a>.
14.g(-2)<g(0)<f (-1) 已知f (x)-g(x)=
①
把上式中的x换成-x,得-f (x)-g(x)=
.
②
由①②解得:f (x)=
,g(x)=-,
从而 g(-2)<g(0)<f (-1).
15.0 (数形结合)在坐标系作出函数y=［x］的图象(如图所示)，显然，直线y=x-1与之无交点.
|
，
，
于是
，
，
故g(2)=4，g(5)=-3，g(-2)=7.
17.解 (1)∵
,
∴k>0时，定义域为(0,+∞);k<0时，定义域为(-1,0).
(2)f (x)=g(x)
lg(kx)=lg(x+1)
=x+1.在定义域范围内有且只有一个解，
令
,
=x+1.
当k>0时，x>0,则,=x+1的图象如图①,由方程
,令Δ=0得k=4或k=0（舍）.∴k=4时，方程在定义域范围内有一解.
又k<0时，-1<x<0.此时，,=x+1的图象如图②,结合图象，k<0成立.
综上可知:k<0或k=4时，方程f (x)=g(x)有且只有一解.
|
.18.解 (1)由f (x)=
※
设方程※的两根为，.依题意
,且<0，从而b-2=0，-a<0.
∴a、b满足的条件为:b=2,a>0.
|
，
∴当a=3时，f (x)=
=2-
，
其图象的对称中心为(-2，2)，如图所示，
由>2知点C在双曲线的上支上.
依题意，A、B所在直线方程为:y=x.
要使点C到直线y=x的距离d最小，
点C(x,y)满足
解出C(-3，3)，
此时
.
方法2 设C(x,y)，由y>2，即
，
设C到直线y=x的距离为d，
则d＝
,
令t=x+2,t<0，
则d=
，
当且仅当-t=-
(t<0)，即t=-1时取“＝”号，此时
，
，即C(-3，3).
19.(1)证明 设0<<<+∞，f ()-f ()＝
，
∵0<<，∴-<0，·>0，∴f ()-f ()<0即f ()<f ()，
∴f (x)=在(0，+∞)上为增函数.
(2)解 ∵f (x)在(0，+∞)上为增函数，∴若f (x)在［m,n］上的值域为［m,n］，
则
，则m、n为方程f (x)=x的两相异实根.
由
，则Δ＝1-4>0-
，
又a>0，∴0<a<.
(3)f (x)≤2x,即≤2x,即
≤2x+
，
∵2x+≥2
＝2，(x=
时取“＝”)，
∴要使≤2x+恒成立，则只需≤2，∴a≥
.
20.解 (1)若按原来投资环境，由p=-知，当x=40时，
，即每年只需从60万元专款中拿出40万元投资，可获最大利润10万元，这样十年的总利润最大值为w=10×10＝100(万元).
(2)若对该产品开发:前5年可用于对产品的投资只有30万元，而p＝f (x)=-在［0,30］上递增，
∴
.
前5年的总利润:
(万元).
设后5年，x万元用于本地销售投资，(60-x)万元用于异地销售投资，则总利润:
=［-］×5+(-
)×5=5［-
+900］，
当x=30时，
＝4 500，
∴10年总利润最大值为
+＝
+4 500，
而+4 500>100，故该项目具有极大的开发价值.
21.分析 条件<2<<4实际上给出了f (x)=x的两个实根所在的区间，因此可以考虑利用上述图象特征去等价转化.
(1)证明 设g(x)=f (x)-x=
,则g(x)=0的两根为和.
由a>0及<2<<4,可得
，即
,
即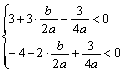
,两式相加得
,所以
.
(2)解 由
=
,可得2a+1=
.
又
,所以,同号.
∴<2,-=2等价于
或
即
或
解之得b<或b>
.
点评 本题主要考查二次函数f (x)的图象的连续性，且由于二次方程至多有两个实数根，所以存在实数m、n使得m<n且f (m)f (n)<0在区间(m,n)上，必存在f (x)=0的惟一的实数根.
22.(1)解 由f (0)=f (1)=f (-1)知c=1,a+b+c=1,a-b+c=1，∴
，
即4(a+c)b=0.∵b≠0，∴a+c=0，即a=-c.
又∵a>0，∴a=1,c=-1，此时b=±1,
∴f (x)=
±x-1.
于是f (x)=
≥-，∴
.
(2)解 依题意
，即b=-2a，∵a>0且b≠0,
∴b<0.令f (x)=0两根为、，则函数y=f (x)的图象与x轴的两个交点为(，0)、(,0)，且+=2,＝
，满足题设的充要条件是:
，
∴a>0，c≤0，b<0且b=-2a为所求.
(3)证明 ∵2b=(a+b+c)-(a-b+c)≤a+b+c+a-b+c≤2，
∴b≤1,又b≤a，∴
又c=f (0)≤1，
，
而f (x)表示开口向上的抛物线，且x≤1，则f (x)最大值应在x=1或x=-1或x=-
时取到.
因为f (-1)≤1，f (1)≤1，
，故f (x)≤得证.