第二章函数热身训练题
一. 教学内容:
第二章函数热身训练题
【模拟试题】(答题时间:90分钟)
§2.1 映射与函数
1. 设![]() 是集合A到B的映射,下列命题中真命题是( )
是集合A到B的映射,下列命题中真命题是( )
A. A中不同元素必有不同的象 B. B中每一个元素在A中必有原象
C. A中每一个元素在B中必有象 D. B中每一个元素在A中的原象唯一
2. 给定映射![]() ,在映射
,在映射![]() 下,
下,![]() 的原象为( )
的原象为( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
3. 已知函数①![]() ②
②![]()
![]() ③
③![]()
④ ,那么是从定义域到值域的一一映射的有( )
,那么是从定义域到值域的一一映射的有( )
A. ①②③ B. ①③④ C. ②③④ D. ①②④
4. 集合![]() ,
,![]() ,那么可建立从A到B的映射的个数是_______,从B到A的映射的个数是______。
,那么可建立从A到B的映射的个数是_______,从B到A的映射的个数是______。
5. 已知![]() ,则
,则![]() __________ 。
__________ 。
6. 下列四组函数,表示同一函数的是( )
A. ![]() ,
,![]()
![]() )
)
B. ![]() ,
,![]()
C. ![]()
![]() ,
,![]()
![]()
D. ![]() ,
,![]()
7. 设集合A和B都是正整数集合![]() ,映射
,映射![]() 把集合A中的元素
把集合A中的元素![]() 映射到集合B中的元素
映射到集合B中的元素![]() ,则在映射
,则在映射![]() 下,象20的原象是( )
下,象20的原象是( )
A. 2 B. 3 C. 4 D. 5
8. 已知曲线C是![]()
![]() 的图象,则( )
的图象,则( )
A. 直线![]() 与C可能有两个交点 B. 直线
与C可能有两个交点 B. 直线![]() 与C至多有一个交点
与C至多有一个交点
C. 直线![]() 与C有且只有一个交点
D. 直线
与C有且只有一个交点
D. 直线![]() 与C不可能有两个交点
与C不可能有两个交点
9. 集合![]() 正整数
正整数![]() ,集合
,集合![]() ,
,![]() 是集合A到集合B的映射,则
是集合A到集合B的映射,则![]() 的原象是________。
的原象是________。
10. 设 ,则
,则![]() _________。
_________。
11. 设A到B的映射![]() ,B到C的映射
,B到C的映射![]() ,则A到C的映射
,则A到C的映射![]() _______。
_______。
12. 1992年世界人口达到![]() 亿,若人口的年平均增长率为
亿,若人口的年平均增长率为![]() ,到2000年底,世界人口数为
,到2000年底,世界人口数为![]() 亿,那么
亿,那么![]() 与
与![]() 的函数关系为_________。
的函数关系为_________。
13. ![]() 中,
中,![]() ,
,![]() ,P、Q分别是AB、AC上的动点,且满足
,P、Q分别是AB、AC上的动点,且满足![]() ,若设
,若设![]() ,
,![]() 。(1)写出
。(1)写出![]() 的取值范围;(2)求
的取值范围;(2)求![]() 的解析式;(3)作出
的解析式;(3)作出![]() 的图象
的图象
§2.2 函数解析式
1. ![]() ,则
,则![]() _______,若
_______,若![]()
![]() 且
且![]() ,则
,则![]() ______。若
______。若![]() ,则
,则![]() _________。
_________。
2. 已知![]() ,则
,则![]() __________。
__________。
3. 若![]() ,
,![]() ,
,![]() ,则
,则![]() __________。
__________。
4. 已知![]() ,
,![]() ,若
,若![]() ,则
,则![]() ________。
________。
5. 已知![]() ,则
,则![]() __________。
__________。
6. 已知![]() ,则
,则![]() ___________。
___________。
7. 若![]() ,
,![]()
![]() ,则
,则![]() 的值是( )
的值是( )
A. 1 B. 3 C. 15 D. 30
8. ![]() 满足
满足![]() ,且
,且![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 设函数![]() 满足
满足![]() ,其中
,其中![]() ,
,![]() ,求
,求![]() 。
。
10. 已知对一切![]() ,都有
,都有![]() ,且方程
,且方程![]() 有5个不同的实根,求这五个根的和。
有5个不同的实根,求这五个根的和。
11. 定义在![]() 上的增函数
上的增函数![]() 满足
满足![]() ,
,![]() ,(1)求
,(1)求![]() 、
、![]() 的值;(2)若
的值;(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
12. 已知函数![]() 满足
满足![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 及
及![]() 的值。
的值。
13. 已知![]() ,
,![]() ,函数
,函数![]() 表示
表示![]() 在
在![]() 上的最大值,求
上的最大值,求![]() 的表达式。
的表达式。
§2.3 函数的定义域
1. 函数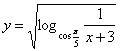 的定义域是( )
的定义域是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 若函数![]() 的定义域是
的定义域是![]() ,则函数
,则函数![]() 的定义域( )
的定义域( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
3. 函数![]() 的定义域是_________,函数
的定义域是_________,函数![]() 的定义域是______。
的定义域是______。
4. 函数![]() 的定义域是________。
的定义域是________。
5. 若函数![]() 的定义域是
的定义域是![]() ,则函数
,则函数![]() 的定义域为_____。
的定义域为_____。
6. 函数![]() 的反函数
的反函数![]() 的定义域是_________。
的定义域是_________。
7. 函数 的定义域为_________ 。
的定义域为_________ 。
8. 函数![]() 的定义域为_________,
的定义域为_________,![]() 的定义域为__________。
的定义域为__________。
9. 已知![]() 的定义域为
的定义域为![]() ,则
,则![]() 的定义域为_________。
的定义域为_________。
10. 若函数![]() 的定义域为R,则实数
的定义域为R,则实数![]() 的取值范围为_________。
的取值范围为_________。
11. 求下列函数的定义域
(1)![]()
(2)![]()
(3)![]()
12. 若函数![]() 的定义域为R,求实数
的定义域为R,求实数![]() 的取值范围。
的取值范围。
§2.4 函数值域
1. 函数![]() (
(![]() ,
,![]() )的值域是
。
)的值域是
。
2. 函数![]() 的值域是
,
的值域是
,![]() 的值域是 。
的值域是 。
3. 函数![]() 的值域是
,
的值域是
,![]() 的值域是 。
的值域是 。
4. 函数![]() 的值域是 ,
的值域是 ,![]() 的值域是
。
的值域是
。
5. 函数![]() 的值域是
。
的值域是
。
6. 若函数![]() 的定义域和值域都是
的定义域和值域都是![]() ,则
,则![]() 的值为 。
的值为 。
7. 函数![]() 的值域是( )
的值域是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 值域是(0,![]() )的函数是( )
)的函数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 函数![]() 的值域是 ,函数
的值域是 ,函数![]() 的值域是 。
的值域是 。
10. 函数![]() 的值域是 ,
的值域是 ,![]() 的值域是 ,函数
的值域是 ,函数![]() 的值域是 。
的值域是 。
11. 求下列函数的值域
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)![]()
12. 求函数![]() 的值域。
的值域。
13. 求函数![]() 的值域。
的值域。
14. 已知![]() ,求
,求![]() 的值域。
的值域。
15. 求函数![]() 的值域。
的值域。
16. 设![]() 的值域为
的值域为![]() ,求
,求![]() 、
、![]() 的值。
的值。
17. 已知![]() 的值域为
的值域为![]() ,求
,求![]() 的值域。
的值域。
【试题答案】
§2.1 映射与函数
1. C 2.
B 3. C 4. 9;8 5. ![]() 6. D 7. C 8. B 9. 8
6. D 7. C 8. B 9. 8
10.![]() 11.
11. ![]() 12.
12. ![]()
13.(1)![]() (2)
(2)![]() (3)
(3)
§2.2 函数的解析式
1. ![]() ;
;![]() ;
;![]() 2.
0 3. 29 4. 1 5.
2.
0 3. 29 4. 1 5. ![]()
6. ![]() 7. C 8. B
7. C 8. B
9. 令![]() ,则
,则![]() ①
①
令![]() ,则
,则![]() ②
②
由①②得![]() 令
令![]() 可得
可得![]()
10. ![]()
![]() 以
以![]() 为对称轴,故五根之和为
为对称轴,故五根之和为![]()
11.(1)![]()
![]()
(2)∵ ![]() ∴
∴ ![]()
∵
![]() 定义在
定义在![]() 上的增函数 ∴
上的增函数 ∴ ![]() 且
且![]() ∴
∴ ![]()
12. ![]()
![]() 令
令![]() 则
则![]()
∴
![]() ∵
∵ ![]() ∴
∴![]()
令![]() 则
则![]() ∴
∴ ![]()
令![]() 则
则![]() ∴
∴ ![]()
13.  对称轴
对称轴![]()
(1)![]()
![]() 即
即![]() 时
时
(2)![]() 时,
时,![]()
(3)![]() 即
即![]() 时
时
①
![]()
![]() 即
即![]() 时
时
②
![]()
![]()
即![]() 时
时
综上
§2.3 函数的定义域
1. B 2.
A 3. ![]() 或
或![]() ;(
;(![]() ) 4.
) 4. ![]()
5. ![]() 6.
6. ![]() 7.
7. ![]() 8.
8. ![]() ;
;![]()
9. ![]() 10.
10. ![]()
11.
(1)![]()
![]() ∵
∵ ![]()
∴
![]() ∴
∴ ![]()
![]()
∴
![]()
(2)![]() ①
① ![]() 时,∵
时,∵ ![]() ∴
∴ ![]()
∴
![]()
②
![]() 时,∵
时,∵ ![]() ∴
∴ ![]()
∴
![]() 综上
综上![]()
(3)![]() ∵
∵ ![]() ∴
∴ ![]()
又
∵ ![]() ∴
∴ ![]() 其中
其中![]()
∴
![]()
12. ![]() 在
在![]() 上恒大于0 ∴
上恒大于0 ∴ ![]()
∴
![]() ∴
∴ ![]()
![]() 也适合故
也适合故![]()
§2.4 函数值域
1. ![]() 2.
2. ![]() ;
;![]() 3.
3. ![]() ;
;![]()
4. ![]() ;
;![]()
5. ![]()
6. 3 7.
B 8. B 9. ![]() ;(0,1) 10.
;(0,1) 10. ![]() ;
;![]() ;
;![]()
11.
(1)![]()

(2)![]()
![]() ∴
∴ ![]()
(3)![]()
![]()
![]()
(4)![]()
(5)令![]()
![]()

![]()
12. ∵ ![]() ∴
∴ ![]()
![]() ∴
∴ ![]()
13. ∵ ![]() ∴
∴ ![]()
![]()
![]()
∴ ![]()
14. ![]() ∴
∴ ![]()
![]()
![]() ∴
∴ ![]()
15. ![]()
![]()
![]()
∵ ![]() ∴
∴ ![]() ∴
∴ ![]()
16. ![]()
![]()
![]()
∴
![]() 又 ∵
又 ∵ ![]() ∴
∴ ![]()
![]() ∴
∴ ![]() ,
,![]()
17. 令![]() 由已知
由已知![]() ,
,![]() 故
故![]()