专题考案(1)函数板块 第2课 函数的性质
(时间：90分钟 满分：100分)
题型示例
已知函数f(x)是在R上的偶函数，且满足f(x+1)+f(x)=1,当x∈［1,2］时，f(x)=2-x，则f(-2004.5)的值为( )
A.0.5 B.1 C.1.5 D.-1.5
分析 ∵函数f(x)是R上的偶函数，∴f(-x)=f(x).由f(x+1)+f(x)=1,得f(-x+1)+f(-x)=1，故f(x+1)=f(1-x),所以函数f(x)关于x=1对称.又由函数f(x)是在R上的偶函数，故函数f(x)又关于y轴对称，由此作图，如图所示可得f(-2004.5)=0.5,故选A.
 |
答案 A
点评 本题主要考查函数的周期性、奇偶性.利用数形结合的方法可迅速解决问题.
一、选择题(8×3′＝24′)
1．函数y=x2+bx+c［x∈［0,+∞
］是单调函数的充要条件是
( )
A.b≥0 B.b≤0 C.b>0 D.b<0
2．函数f(x)=4x2-mx+5在区间［-2,+∞上是增函数，M=f(1)，则下列不等式或等式成立是( )
A.M≥25 B.M=25 C.M≤25 D.M>25
3．定义在R上的函数f(x)、g(x)都有反函数,且f(x+1)和g-1(x-2)的图象关于直线y=x对称，若g(15)=2000,则f(16)的值为 ( )
A.1999 B.2000 C.2001 D.2002
4．函数f(x)=x-
在(1，+∞)上是增函数，则实数a的取值范围是
( )
A.a≥0 B.a≥1 C.a≥-2 D.a≥-1
5．已知定义在R上的函数f(x)满足f(x-1)=f(x+1),f(1-x)=f(1+x),且在［-1,0］上单调递增.设a=f(3),b=f(),c=f(2),则a、b、c的大小关系是 ( )
A.a>b>c B.a>c>b C.b>c>a D.c>b>a
6．函数y=f(x)有反函数y=f－1(x)，把y=f(x)的图象在直角坐标平面内绕原点顺时针方向转动90°后得到的图象对应的函数是 ( )
A.y=f－1(-x) B.y=f－1(x) C.y=-f－1(-x) D.y=-f－1(x)
7．定义在R上的函数f(x)满足f(x)=f(x+2),当x∈［3,5］时，f(x)=2-x-4,则 ( )
A.
B.f(sin1)>f(cos1)
C.
D.f(cos2)>f(sin2)
8．已知函数f(x)是定义在R上的奇函数，当x<0时，f(x)=(
)x，那么f－1(-9)的值是( )
A.-2 B.2 C.-3 D.3
二、填空题(5×3′＝15′)
9．已知f(x)是定义在R上的偶函数，且它在［0，+∞］上单调递增，那么使不等式f(-2)≤f(a)的实数a的取值范围是 .
10．函数f(x)=logcos50°x2-2x-3的增区间为 .
11．关于函数f(x)=lg
(x≠0),有下列命题：
①函数y=f(x)的图象关于y轴对称;
②当x>0时，f(x)是增函数，当x<0时，f(x)是减函数;
③函数f(x)的最小值为lg2;
④当-1<x<0或x>1时，f(x)是增函数;
⑤f(x)无最大值，也无最小值.
其中正确的命题是 .
12．函数f(x)=
(α为常数)的图象过点(4,
),那么f-1(8)的值是
.
13．函数f(x)=loga(x+
)(x≥1)(0<a<1)的反函数是f－1(x)=
.
三、解答题(5×10′＝50′)
14．已知关于n的不等式
对一切大于1的自然数n都成立,试求实数a的取值范围.
15．f(x)是定义在(0,+∞)上的增函数，且f(
)=f(x)-f(y).
(1)求f(1)的值.
(2)若f(6)=1,解不等式f(x+3)-f(
)<2.
16．已知函数f(x)=(
)2(x≥1)，f－1(x)是f(x)的反函数，记g(x)=
+2，求：
(1)f－1(x)的定义域与单调区间.
(2)g(x)的最小值.
17．设偶函数f(x)在区间［a,b］上是增函数(a>0)，试判定函数F(x)=()f(x)-x在区间［-b,-a］上的单调性，并加以证明.
18．给定函数f(x)=logalogax(a>0且a≠1).
(1)求函数的定义域.
(2)当f(x)>1时，求x的取值范围.
(3)当x>1时，判断函数f(x)的单调性，并证明你的结论.
四、思考与讨论(11′)
19．设a>0,f(x)=
是R的偶函数.
(1)求a的值;
(2)证明f(x)在(0,+∞)上为增函数.
参考答案
1．A
函数y=x2+bx+c的单调增区间是［-
,+∞.
∵所求函数的定义域为x∈［0,+∞,
∴此函数单调的充要条件是-≤0
b≥0.
2．A
依题意，
≤-2
m≤-16，则M=f(1)=9-m≥25.
3．D 设y=g-1(x-2)，由反函数的概念得x=g(y)+2,即y=g-1(x-2)的反函数为y=g(x)+2,从而f(x+1)=g(x)+2.当x=15时，f(16)=g(15)+2=2002.故选D.
4．D 由单调性的定义即得.
5．D 由f(x-1)=f(x+1)可推出f(x+2)=f(x),即f(x)以2为一个周期.a=f(3)=f(1)=f(-1),
b=f(
)=f(-2) c=f(2)=f(0),又∵f(x)在［-1,0］上单调递增,∴c>b>a.
6．Ｄ 设(x,y)是y=f(x)图象上任意一点，当把y=f(x)的图象绕原点顺时针方向转动90°后其对应点为(X,Y)，则X＋9i=(x+yi)·(-i)=y-xi，故y=X,x=-Y,于是X=f(-Y)-Y=f-1(X)即y=-f－1（x）.
7．D ∵f(x)=f(x+2),∴F=2是其一个周期.设x∈［-1,1］,则x+4∈［3,5］,
f(x)=f(x+4)=2-x+4-4=2-x其图象如图所示.
A:0<sin
<1,∴
B:0<cos1<sin1<1,∴f(sin1)<f(cos1)
C:cos
，
D:cos2=sin
,∴f(cos2)=f
sin2=sin(π-2),∵1>sin(π-2)>sin
>0
∴
>f［sin(π-2)］,即:f(cos2)>f(sin2)故正确答案是D.
8．Ｂ
当x>0时，f(x)=-()-x，设f-1（-9）=a，则f(a)=-9-()－a=-9a=2.
9．a≤-2或a≥2
f(-2)≤f(a)f(-2)≤f(a)a≥2.
10．(-∞,-1)，［1,3］ 作函数u(x)=x2-2x-3的图象判断.
11．①③④ f(x)是偶函数，且f(x)=lg(x+
)≥lg2，可由f(x)的奇偶性确定单调区间，即先判断出f(x)在(0，+∞)上的单调性.
12．
将(4,)代入f(x)=,得=
,∴α=
,
∴f(x)=
=8得x=.
13．(ax+a-x)(x≤0) 注意注明反函数的定义域.
14．解 设f(n)=
(n∈N且n≥2),
∵f(n+1)-f(n)=
>0,
∴f(n)是关于n的单调增函数，且当n≥2时,f(n)≥f(2)=
,
故要使f(n)>
loga(a-1)+
对一切n≥2,n∈N恒成立,
则需且仅需
loga(a-1)+,即loga(a-1)<-1,
又a-1>0,∴0<a-1<
,解得1<a<
.故所求a的取值范围为{a1<a<}.
点评 利用函数的单调性求参数的取值范围.
15．解 (1)令x=y,得f(1)=0.
(2)由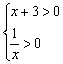
，得x>0.由f(6)=1及f(x+3)-f()<2，得f［x(x+3)］<2f(6)，
即f［x(x+3)］-f(6)<f(6)，即f 
<f(6).
∵f(x)在(0，+∞)上递增，∴
<6且x>0，
解得
0<x<
.
16．解 (1)∵x≥1,∴0≤<10≤()2<1.
∴0≤y<1,且=
x=
.
∴f－1（x）=
(0≤x<1).原函数递增，f-1(x)也递增．
(2)g(x)=
当且仅当1+
即x=3-2∈［0,1］时取“＝”.
∴g(x)的最小值为2.
17．解 ∵f(x)是偶函数且在区间［a,b］上单调递增(a>0)，∴f(x)在区间［-b,-a］上单调递减，f(x)-x在［-b,-a］上也单调递减，故F(x)=()f(x)-x在［-b,-a］上单调递增.
证明(略)(提示:作商
与1比较大小).
18．解 (1)由logax≠0，知函数的定义域为(0，1)∪(1,＋∞).
(2)由logalogax>1，则当0<a<1时，0<logax<a，解得x∈(aa,1)∪(1,a-a)；
当a>1时，logax>a，解得x∈(0,a-a)∪(aa,+∞).
(3)任取1<x1<x2,则f(x2)-f(x1)=loga
=logalogx1x2.
又logx1x2>logx1x1=1logx1x2>1，∴当0<a<1时，f(x2)-f(x1)<0，
故f(x)在(1，＋∞)单调递减；
当a>1时,f(x2)-f(x1)>0，故f(x)在(1，+∞)单调递增.
19．(1)解 因为f(x)=是R上的偶函数,所以f(-x)=f(x).
取x=1,则f(-1)=f(1),即
,所以1+e2a2=e2+a2,
所以(1-e2)(1-a2)=0,所以1-a2=0,又a>0故a=1.
(2)证明 因为a=1,所以f(x)=ex+
,任取x1,x2∈(0,+∞),且x1<x2,则
=
.
由x1,x2∈(0,+∞)知ex1+x2-1>0,由x1<x2知ex1-ex2<0,
所以f(x1)<f(x2),所以f(x)在(0,+∞)上为增函数.