专题十 三角函数的图像与性质
1.
函数![]() 的最小值和最小正周期分别是(
)
的最小值和最小正周期分别是(
)
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
2.
函数![]() 的最小正周期为( )
的最小正周期为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.
下列函数中周期为2的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.
为了得到函数![]() 的图象,可以将函数
的图象,可以将函数![]() 的图象(
)
的图象(
)
A.向右平移![]() 个长度单位 B.向左平移
个长度单位 B.向左平移![]() 个长度单位
个长度单位
C.向右平移![]() 个长度单位
D.向左平移
个长度单位
D.向左平移![]() 个长度单位
个长度单位
5.
已知函数![]() ,则其最小正周期和图象的一条对称轴方程分别为( )
,则其最小正周期和图象的一条对称轴方程分别为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
6.
已知函数![]() 在
在![]() 上单调递增且在这个区间上的最大值为
上单调递增且在这个区间上的最大值为![]() ,则实数
,则实数![]() 的一个值可以是( )
的一个值可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.
要得到![]() 的图象,且使平移的距离最短,则需将
的图象,且使平移的距离最短,则需将![]() 的图象向______平移______单位,即可得到.
的图象向______平移______单位,即可得到.
8.
函数![]() 取得最大值时,自变量
取得最大值时,自变量![]() 的集合是_____________________________________.
的集合是_____________________________________.
9.
已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
⑴ 当且仅当![]()
![]() 时,
时,![]() 取得最小值
取得最小值
⑵ ![]() 是周期函数
⑶
是周期函数
⑶ ![]() 的值域是
的值域是![]()
⑷ 当且仅当![]()
![]() 时,
时,![]()
其中正确的结论序号是____________(把你认为正确的结论的序号都填上).
10.
设函数![]()
![]() ,
,![]() ,给出以下四个结论:
,给出以下四个结论:
⑴ 它的周期为![]() ;
⑵ 它的图象关于直线
;
⑵ 它的图象关于直线![]() 对称;
对称;
⑶ 它的图象关于点![]() 对称; ⑷ 在区间
对称; ⑷ 在区间![]() 上是增函数.
上是增函数.
以其中两个论断作为条件,另外两个论断作为结论,写出你认为正确的一个命题:_________________________.
11.
已知函数![]()
![]() .
.
⑴ 求函数![]() 的最小正周期和最大值;
的最小正周期和最大值;
⑵ 函数![]() 的图象可由
的图象可由![]()
![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
12.
设函数![]() ,其中
,其中![]() .
.
⑴ 若![]() 的周期为
的周期为![]() ,求当
,求当![]() 时
时![]() 的值域;
的值域;
⑵ 若函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ,求
,求![]() 的值.
的值.
13.
已知函数![]() ,
,![]() .
.
⑴ 求实数![]() ;
;
⑵ 求函数![]() 的最小正周期及单调增区间;
的最小正周期及单调增区间;
⑶ 若函数![]() 的图象按向量
的图象按向量![]() 平移后,得到函数
平移后,得到函数![]() 的图像,求
的图像,求![]() 的解析式.
的解析式.
14.
已知向量![]() ,
,![]() ,定义函数
,定义函数![]() .
.
⑴ 求函数![]() 的最小正周期;
的最小正周期;
⑵ 求函数![]() 的单调减区间;
的单调减区间;
⑶ 画出函数![]() ,
,![]() 的图象,由图象研究并写出
的图象,由图象研究并写出![]() 的对称轴和对称中心.
的对称轴和对称中心.
1.A 2.B 3.C 4.A 5.D 6.C
7.左、![]() 8.
8.![]() ,
,![]() 9.⑵⑷
9.⑵⑷
10.⑴⑵![]() ⑶⑷ 或 ⑴⑶
⑶⑷ 或 ⑴⑶![]() ⑵⑷
⑵⑷
11.解:(1)![]()
![]() )
)
∴T=![]()
(2)先将![]() )的图象向左移
)的图象向左移![]() 个单位,得到
个单位,得到![]() 的图象;再将
的图象;再将![]() 的图象的横坐标变为原来的一半,纵坐标不变,得到
的图象的横坐标变为原来的一半,纵坐标不变,得到![]() 的图象.
的图象.
或先将![]() )的图象的横坐标变为原来一半,纵坐标不变,得到函数
)的图象的横坐标变为原来一半,纵坐标不变,得到函数
![]() 的图象;再将
的图象;再将![]() 的图象向左移
的图象向左移![]() 个单位,得到
个单位,得到![]() 的图象.
的图象.
12.解:![]()
![]()
(I)因为![]() ,
,
![]() ,
,
所以,![]() 的值域为
的值域为![]() .
.
(II)因为![]() 的一条对称轴为
的一条对称轴为![]()
![]()
![]() .
.
13.(1)∵f(![]() )=0 ∴2cos2
)=0 ∴2cos2![]() +asin
+asin![]() cos
cos![]() =0 ∴a=-2
=0 ∴a=-2![]()
(2) f(x)=2cos2x-2![]() sinxcosx=cos2x+1-
sinxcosx=cos2x+1-![]() sin2x =2cos(2x+
sin2x =2cos(2x+![]() )+1
)+1
∴T=π
f(x)的单调增区间为[kπ+![]() ,kπ+
,kπ+![]() π](k∈Z)
π](k∈Z)
(3)g(x)=2cos2x
14.15.解:![]()
![]() ………………………………5分
………………………………5分
(1)![]() ……………………………………6分
……………………………………6分
(2)![]()
![]()
![]() ……………………9分
……………………9分
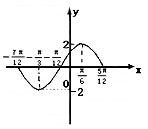
|
从图象上可以直观看出,此函数有一个对称中心(![]() ),无对称轴…………14分
),无对称轴…………14分