08年高中毕业班理科数学教学质量检测
数学试题（理科）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 1500分。考试时间120分钟。
第Ⅰ卷（选择题 共60分）
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、考试号、考试科目涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡
皮擦干净后，再选涂其它答案，不能答在试题卷上。
3．考试结束，监考人将本试卷和答题卡一并收回。
参考公式：
回归直线方程中的回归系数 台体的体积公式
其中S和S′是上、下底面积，h是高
球有表面积和体积公式
其中R表示球的半径
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．在下列直线中，是圆
的切线的是 （ ）
A．x=0 B．y=0 C．x=y D．x=－y
2．
的展开式中
的系数为 （ ）
A．240 B．120 C．60 D．15
3．函数
的零点所在的区间为 （ ）
A．（－1，0） B．（0，1） C．（1，2） D．（1，e）
4．已知
的最大值是 （ ）
A．10 B．12 C．13 D．14
5．曲线
围成的封闭图形的面积是 （ ）
A．
B．2－ C．
D．
6．已知正方体的体积是8，则这个正方体的外接球的体积是 （ ）
|
B．
C．
D．
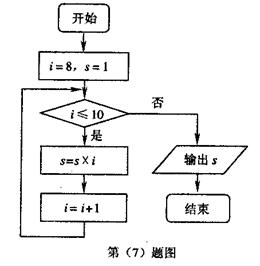
7．右面框图表示的程序所输出的结果是（ ）
A．8 B．9
C．72 D．720
8．如果命题“
”是假命题，则
正确的是 （ ）
A．p、q均为真命题
B．p、q中至少有一个为真命题
C．p、q均为假命题
D．p、q中至多有一个为真命题
9．已知直线m、n平面
，下列命题中正确的是 （ ）
A．若直线m、n与平面
所成的角相等，则m//n
B．若m//,
则m//n
C．若m
，
，m//n，则//
D．若m⊥，n⊥，⊥，则m⊥n
|
|
|
B．
C．
D．
11．要得到函数
的图象，只须将函数
的图象 （ ）
A．向左平移
个单位，再把所有点的横坐标伸长到原来的2倍，纵坐标不变
B．向右平移个单位，再把所有点的横坐标伸长到原来的2倍，纵坐标不变
C．向左平移个单位，再把所有点的横坐标缩短到原来的
倍，纵坐标不变
D．向右平移个单位，再把所有点的横坐标缩短到原来的倍，纵坐标不变
12．抛物线
准线为l，l与x轴相交于点E，过F且倾斜角等于60°的直线与抛物线在x轴上方的部分相交于点A，AB⊥l，垂足为B，则四边形ABEF的面积等于 （ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题，共90分）
|
二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中的横线上。
13．复数
.
14．双曲线
的左右焦点分别为F1、F2，已知线段F1F2被点（b,0）分成5：1两段，则此双曲线的离心率为
.
15．已知x、y为正实数，且
的最小值是
.
16．一个圆台上，下底面的面积分别是
，其母线长为4，则这个圆台的体积等于 .
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17．18．（本小题满分12分）已知在△ABC中，a，b，c分别是角A、B、C所对的边，S是该三角形的面积，若向量
（1）求角B的大小；
（2）若B为锐角，a=6，S=，求b的值。
18．（本小题满分12分）某经营者在一个袋子里放3种不同颜色的小球。每种颜色的球都是3个，然后让玩的人从中一次性摸出5个球并规定如果摸出来的小球的颜色是“221”（即有2种颜色的球各为2个，另一种颜色的球为1个），则玩者要交钱5元；如果摸出来的颜色是“311”，则奖给玩者2元；如果摸出来的颜色是“320”则奖给玩者10元。
（1）求玩者要交钱的概率；
（2）求经营者在一次游戏中获利的期望（保留到0.01元）。
19．（本小题满分12分）某种产品每件成本为6元，每件售价为x元（x>6），年销量为u万件，若已知
与
成正比，且售价为10元时，年销量为28万件。
（1）求年销售利润y关于x的函数关系式；
（2）求售价为多少时，年利润最大，并求出最大年利润。
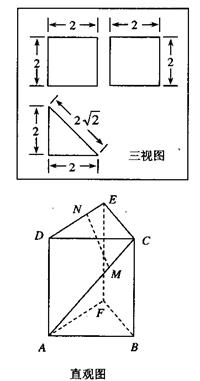
20．（本小题满分12分）多面体ABCDEF的直观图及三视图分别如图所示，已知点M在AC上，点N在DE上，且AM：MC=DN：NE=a
（1）求证：MN//平面BCEF；
|
21．（本小题满分12分）在数列
，已知
（1）记
，求证：数列
是等差数列；
（2）求数列
的通项公式；
（3）对于任意给定的正整数k，是否存在
，使得
若存在，求出m的值；若不存在，请说明理由。
|
的离心率为e，点F为其下焦点，点A为其上顶点，过F的直线
与椭圆C相交于P、Q两点，且满足：
（1）试用a表示
；
（2）求e的最大值；
（3）若
取值范围；
参考答案
一、选择题（本大题共12小题，每小题5分，共60分）
BCBCD BDBDB CC
|
13．
14．
15．9 16．
三、解答题
17．解：（1）由
∴
∴
∴
∴B
（2）由a=6,S=，得
∴c=4。
由
∴
………………12分
18．（本小题满分12分）
解：（1）只有出现的情况是“221”，玩者才需要交钱。
∴玩者要交钱的概率为
……5分
（Ⅱ）设
表示经营者在一次游戏中获利的钱数，则
=5时（即“221”时）
=－2时（即“311”时）
=－10时（即“320”时）
…………9分
|
| －2 | －10 | 5 |
| P |
|
|
|
∴的分布列是（见右侧表）
∴
（元）
∴经营者在一次游戏中获利的期望为1.36元。
…………12分
19．（本小题满分12分）
解：（1）设
∵售价为10元时，年销量为28万件；
∴
∴
∴
…………6分
（2）
令
显然，当
时，
时，
∴函数
上是关于x的增函数；
在
上是关于x的减函数。……………………10分
∴当x=9时，y取最大值，且
∴售价为9元时，年利润最大，最大年利润为135万元。………………12分
20．（本小题满分12分）
解：（1）由三视图可知，该多面体是底面为直角三角形的直三棱柱ABF—DCE。
且AB=BC=AF=2，CE=BF=
，∠BAF=90°
在CD上取一点G，DG：GC=DN：NE，连MG、NG。则
∵AM：MC=DN：NE=a，
∴NG//CE，MG//BC。
∴平面MNG//平面BCEF。
∴MN//平面CDEF。…………………………6分
（2）∵a=1
∴M、N分别是AC、CE的中点。
以AB、AF、AD分别为x轴、y轴、z轴，建立空间直角坐标系，则有关各点的坐标分别是D（0，0，2），F（0，2，0），M（1，1），N（0，1，2）
∴
…………8分
设平面DMN的法向量
∴
∴
∴
设平面MNF的法向量为
∴
∴
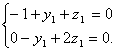
……………………10分
设二面角D—MNF的平面角为
，
则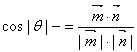
∴二面角D—MN—F的余弦值的绝对值为
………………12分
21．（本小题满分12分）
解（1）∵
∴
∴
∴
∴
又
∴
（2）∵数列是公差为2的等差数列，且
∴
∵
∴
……………………7分
（3）假设对于任意给定的正整数k，存在，使得
则
……………………9分
∵对于任意给定的正整数k，
必为非负偶数，
∴
∴存在
……………………12分
22．（本小题满分14分）
解：（1）联立方程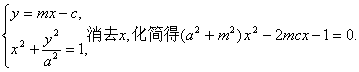
设
……………………3分
∵
∴
∴
………………7分
（2）由（1）知
∴
∴
∴
∴
∴离心率e的最大值为
……………………11分
（3）∵
∴
∴
解得
∴
即
∴m的取值范围是
………………14分