高考数学二轮复习圆锥曲线测试题
一、.填空题（共14小题，每题5分，计70分）
1．抛物线
上一点
的纵坐标为4，则点与抛物线焦点的距离为__________
2．若焦点在x轴上的椭圆
的离心率为
，则m= __________
3．若方程x2+ky2=2表示焦点在y轴上的椭圆, 那么实数k的取值范围是__________
4．设P是双曲线
上一点，双曲线的一条渐近线方程为
,F1、F2分别是双曲线的左、右焦点，若
，则
__________
5．对于抛物线y2=2x上任意一点Q, 点P(a, 0)都满足PQ≥a, 则a的取值范围是
6．若椭圆
的左、右焦点分别为F1、F2，线段F1F2被抛物线y2=2bx的焦点分成5：3两段，则此椭圆的离心率为__________
7．已知双曲线
的一条准线与抛物线
的准线重合，则该双曲线的离心率为__________
8．设A(x1,y1),B(x2,y2)是抛物线y2=2px(p>0)上的两点,并且满足OA⊥OB. 则y1y2等于__
9．已知双曲线
的焦点为F1、F2，点M在双曲线上且
则点
M到x轴的距离为__________
10．设椭圆的两个焦点分别为F1、、F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF为等腰直角三角形，则椭圆的离心率是__________
11．若双曲线的渐近线方程为
，它的一个焦点是
，则双曲线的方程是
12．设中心在原点的椭圆与双曲线2 x2-2y2=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .
13． 过双曲线
(a＞0，b＞0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点，以MN为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于_________．
14．以下同个关于圆锥曲线的命题中
①设A、B为两个定点，k为非零常数，
，则动点P的轨迹为双曲线；
②过定圆C上一定点A作圆的动弦AB，O为坐标原点，若
则动点P的轨迹为椭圆；
③方程
的两根可分别作为椭圆和双曲线的离心率；
④双曲线
有相同的焦点.
其中真命题的序号为 （写出所有真命题的序号）
南京市2008届高三数学二轮复习圆锥曲线测试题
班级 姓名 分数
一、填空题（共14小题，每小题5分，满分70分．）
1、 2、 3
4、 5、 6
7、 8、 9
10、 11、 12
13、 14、
二、解答题（6大题共90分，要求有必要的文字说明和步骤）
15（本小题满分14分）求两条渐近线为
且截直线 
所得弦长为
的双曲线方程。
16．（本小题满分14分）已知在平面直角坐标系
中的一个椭圆，它的中心在原点，左焦点为
,右顶点为
,设点
.
⑴求该椭圆的标准方程；
⑵若
是椭圆上的动点，求线段
中点
的轨迹方程
17（本小题满分15分）
如图所示四棱锥
中，
，
，
，
，为
的中点
（1）求证：
（2）在
内找一点
，使
18．（本小题满分15分）
椭圆
的离心率
，、是椭圆上关于
、
轴不对称的两点，线段
的垂直平分线与轴交于
(1)设的中点为
求
的值
（2）若
为椭圆的右焦点，且
，
求椭圆的方程
o
19（本小题满分14分）
已知椭圆
，
（1）求斜率为2的平行线的中点轨迹方程；
（2）过A（2，1）的直线l与椭圆相交，求l被截得的弦的中点轨迹方程；
（3）过点P（,）且被P点平分的弦所在直线的方程.
20（本小题满分14分）
在平面直角坐标系中，经过点
且斜率为
的直线
与椭圆
有两个不同的交点和
．
（I）求的取值范围；
（II）设椭圆与轴正半轴、轴正半轴的交点分别为
，是否存在常数，使得向量
与
共线？如果存在，求值；如果不存在，请说明理由．
参考答案
1. 
2. m=
3.
4. 7 5.
6. 
7 
8. y1y2 = – 4p2 9. 
10. 
11. 
12. 
13. 2
14. ③④
15略
16.(1)由已知得椭圆的半长轴a=2,半焦距c=
,则半短轴b=1.
又椭圆的焦点在x轴上,
∴椭圆的标准方程为
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0),
| 由 |
| 得 |
|
| y= | y0=2y－ |
x=
x0=2x－1
由,点P在椭圆上,得
,
∴线段PA中点M的轨迹方程是
.
17略 18略
19解(1)设这些平行弦的方程为y=2x+m,弦的中点为M(x,y).
联立直线方程和椭圆方程:y=2x+m,消去y得,
,
因此
=-
,
.
M的坐标是:x=
,y=2x+m,
,消去m得:y=
.
(2)设弦的端点为P(
),Q(
),其中点是M(x,y).
因此:
=
,
化简得:
(去除包含在椭圆内部的部分).
(3)由(2)可得弦所在直线的斜率为k==
,因此所求直线方程是:
y-=-
(x-),化简得:2x+4y-3=0.
20．解：（Ⅰ）由已知条件，直线的方程为
，
代入椭圆方程得
．
整理得
①
直线与椭圆有两个不同的交点和等价于
，
解得
或
．即的取值范围为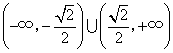
．
（Ⅱ）设
，则
，
由方程①，
． ②
又
． ③
而
．
所以与共线等价于
，
将②③代入上式，解得
．
由（Ⅰ）知或，故没有符合题意的常数．