08届高考理科数学月考试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。考试时间120分钟，满分150分。
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．
等于
A．
B．
C．
D．
2．已知映射
,其中
,对应法则
若对实数
,在集合A中不存在原象,则
的取值范围是
A．
B．
C．
D．
3．已知{
}是等差数列,
,
,则过点（
，
）
| |
A．4
B．
C．— 4
D．
4．已知非零单位向量
、
满足
,则与
的夹角是
A．
B．
C．
D．
5．若关于
的不等式x-2+x+2>
的解是全体实数，则实数的取值范围是
A．
B．
C．
D．
6．函数
是偶函数，且在区间
上单调递减，则
与
的大小关系为
A．
B．
C．
D．不能确定
7．将直线
沿轴向左平移1个单位，所得直线与圆
相切，则实数
的值为
A．－3或7 B．－2或8 C．0或10 D．1或11
8．设
分别是
中
所对边的边长,则直线
与
的位置关系是
A．平行 B．垂直 C．重合 D．相交但不垂直
9．若互不相等的实数a，b，c成等差数列，c，a，b成等比数列，且a+3b+c=10，则a的值为
A．4 B．2,-4 C．－2 D．－4
10．函数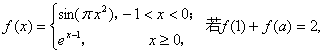
则的所有可能值为
A．1 B．
C．1， D．1，
11．已知命题P：
;命题q:函数
的值域为R ,则P是q的
A．充要条件 B．必要不充分条件
C．充分不必要条件 D．既不充分也不必要条件
12．奇函数
满足：
，且在区间
与
上分别递减和递增，则不等式
的解集为
A．
B．
C．
D．
第Ⅱ卷（非选择题，共20分）
二、填空题：本大题共4小题，每小题5分，共20分
13．若
14．不等式
的解集是
15．若实数x、y满足
，则
的最小值是
16．如图，在直角坐标系中,一质点从原点出发,沿图示箭头方向每秒钟移动一个单位,问第2008秒时质点所在的位置坐标是
三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分10分）
已知函数
的定义域集合是A,函数
的定义域集合是B
（1）求集合A、B
（2）若A
B=B,求实数的取值范围．
18．（本小题满分12分）
已知
（其中
），函数
，若直线
是函数f（x）图象的一条对称轴，
（1）试求
的值；
（2）先列表再作出函数
在区间
上的图象．
19．（本小题满分12分）
为贯彻落实党的十七大精神,加快新农村建设步伐,红星镇政府投资c万元生产甲乙两种商品,据测算,投资甲商品x万元,可获得利润P=x万元,投资乙商品x万元可获得利润Q=40
万元，如果镇政府聘请你当投资顾问，试问对甲乙两种商品的资金投入分别是多少万元？才能获得最大利润,获得最大利润是多少万元？
20．（本小题满分12分）
设圆满足:（1）截直线y=x所得弦长为2;（2）被直线y=－x分成的一段劣弧所在的扇形面积是圆面积的倍．在满足条件（1）、（2）的所有圆中,求圆心到直线x+3y=0的距离最小的圆的的方程．
21．（本小题满分12分）
已知函数
，
（1）求函数的最小值；
（2）若
，求证：
．
22．（本小题满分12分）
已知数列
中
，其前n项和为 满足
．
（1）试求数列
的通项公式．
（2）令
是数列
的前n项和，证明：
．
（3）证明:对任意的
，均存在
，使得（2）中的
成立．
参考答案
一．BBCAA CABDC CD
二．（13）．3; （14）．（-1,0]; （15）,6 16．（-31，7）
17．（1）A＝
……………（3分）
B＝
……………………（6分）
（2）由A
B＝B得A
B，因此
…………………………（8分）
所以
,所以实数ａ的取值范围是
…………………………（10分）
18．
………………（4分）
（1）
直线为对称轴，
，
，
……（6分）
（2）
|
|
|
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | -1 | 1 | 3 | 1 | 0 |
………………（9分）
函数f（x）在
的图象如图所示。
……（12分）
19．设对甲厂投入x万元（0≤x≤c）,则对乙厂投入为c—x万元．所得利润为
y=x+40
（0≤x≤c） ……………………（3分）
令=t（0≤t≤
）,则x=c－t2
∴y=f（t）=－t2+40t+c=－（t—20）2+c+400……………………（6分）
当≥20,即c≥400时,则t=20, 即x=c—400时, ymax =c+400… （8分）
当0<<20, 即0<c<400时,则t=,即x=0时,ymax=40
．…（10分）
答：若政府投资c不少于400万元时,应对甲投入c—400万元, 乙对投入400万元,可获得最大利润c+400万元．政府投资c小于400万元时,应对甲不投入,的把全部资金c都投入乙商品可获得最大利润40万元．…（12分）
20．设所求圆的圆心为P（a,b）,半径为r,
则P到直线y=x、直线y=－x的距离分别为
、
．………（2分）
由题设知圆P截直线y=－x所得劣弧所对圆心角为90°,
圆P截直线y=－x所得弦长为
r,故r2=
（）2，
即r2=（a+b）2，……………………（4分）
又圆P截直线y=x所得弦长为2，所以有r2=1+
,
从而有
．……………………（6分）
又点P到直线x+3y=0的距离为d=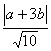
,
所以10d2=a+3b2=a2+6ab+9b2=8b2+2≥2……………………（8分）
当且仅当b=0时上式等号成立,
此时5d2=1,从而d取得最小值,由此有a=±,r=．…………（10分）
于是所求圆的方程为（x－）2+y2=2或（x－）2+y2=2…………（12分）
21．（1）
=
，………………2分
当
时，
，所以当时，
，
则函数在
上单调递增，
所以函数的最小值
；…………………………5分
（2）由（1）知，当
时，
，
∵
，
∴
，
①……7分
∵
，
∴
②………………………10分
由①②得 …………………………12分
22．（1）由得
，
，即
又
，
故数列的通项公式为
．……………………（4分）
（2）
……………………（8分）
（3）证明：由（2）可知
若
,则得
,化简得
，
当
，即
………………（10分）
当
，即
，取
即可,
综上可知,对任意的
均存在
使得时（2）中的成立（12分）