08届高考理科数学模拟测试试题（2008.3.3）
一. 选择题（每小题5分，共60分）
1．复数
在映射
下的象是
，则
的原象是（ ）
A． 
B. 
C. 
D. 2
2．已知随机变量
，若
，则
（ ）
Ａ.0 B.1 C.2 D.4
3.已知
、
是不同的两个平面，直线
，直线
，命题
：
与
没有公共点；命题
：
，则是的（ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件
4．三棱锥
中，
、
、
两两互相垂直，且
，
，则空间一点
到点
、
、
、
等距离
的值是 ( )
A．
B．
C．
D． 
5. 已知为直角坐标系原点，、
的坐标均满足不等式组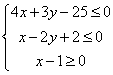
，则
的最小值等于(
)
A． B．
C．
D．0
6.已知
，
若
为满足
的一随机整数，则
是直角三角形的概率是 ( )
A．
B．
C．
D．
7. 数列
满足：
，
且
对于任何的正整数
成立，则
的值为（ ）
A．5032 B．5044 C．5048 D．5050
8.若函数
的导数是
，则函数
的的单调递减区间是 ( )
A．
B．
C．
D．
9. 有两排座位，前排11个座位，后排12个座位，现安排2个人就坐，规定前排中间的3个座位不能坐，并且这2个人不左右相邻，那么不同的坐法种数是( )
A．234 B．346 C．350 D．363
10. 若
，则常数、的值为( )
A．
B．
C．
D． 
11. 曲线
与直线
有两个公共点，则实数的取值范围是（ ）
A．
B．
C．
D．
12．函数
的最大值与最小值依次为
、
，则（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
二、填空题：(每小题4分，共16分)
13.已知是双曲线
右支上的一点，双曲线的一条渐近线方程为
，设
、
分别为左、右焦点，若
，则
.
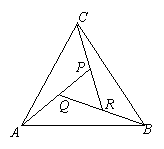
14.如图，在中，设
，
，
的中点为，
的中点为
，
的中点为，则用
、
表示
的式子为
.
15.已知一个半径为
的球中有一个各棱长都相等的正三棱柱，则这个正三棱柱的体积是 .
16. 曲线
上的点到原点的距离的最小值是 .
三、解答题（本大题共6小题，共74分，解答应写出必要的文字说明或演算步骤）
17.(本小题满分12分)
已知向量
，
，其中为坐标原点.
（1）若
，求向量
与
的夹角.
（2）若
对任意实数、都成立，求实数
的取值范围.
18．(本小题满分12分)最近，李师傅一家三口就如何将手中的10万元钱进行投资理财，提出了三种方案：
第一种方案：李师傅的儿子认为，根据股市收益大的特点，应该将10万全部用来买股票，据分析预测：投资股市一年可能获利
，也可能亏损
（只有这两种可能），且获利的概率为.
第二种方案：李师傅认为，现在股市风险大，基金风险较小，应该将10万全部用来买基金，据分析预测：投资基金一年后可能获利，可能亏损
，也可能不赔不赚，且这三种情况发生的概率分别为
、
、.
第三种方案：：李师傅的妻子认为，投资股市、基金均有风险，应该将10万全部存入银行一年，现在存款年利率为
，存款利息税率为
.
针对上述三种投资方案，请你为李师傅家选择一种合理的理财方案，并说明理由.
19．(本小题满分12分)已知椭圆的焦点在
轴上，它的一个顶点恰好是抛物线
的焦点，椭圆的离心率等于
.
（1）求椭圆的方程；
（2）过椭圆的右焦点
作直线
交椭圆于、两点，交
轴于点，若
，
，求证：
为定值.
20．(本小题满分12分)如图，直三棱柱
中，
，
，
，
为棱
上的一动点，、分别为
、
的重心.
（1）求证：
；
（2）若二面角
的大小为
，求点
到平面
的距离.
（3）若点在上的射影正好为，试判断点在上的射影是否为，并说明理由．
21．(本小题满分12分)
已知
是定义在上的奇函数，当
时，
，
.
（1）求的解析式；
（2）求实数，使得当
时，的最小值是3.
（3）设
，
，求证：当
时，
．
22. (本小题满分14分)
已知
.
（1）设
展开式中项的系数为
，求；
（2）设展开式中
项的系数为
，求证：
；
（3）是否存在常数、，使
对一切
，
恒成立？如果存在，求出的值；如果不存在，说明理由
参考答案
一. 选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | C | A | C | B | C | B | C | B | B |
二、填空题：(每小题4分，共16分)
13、5； 14、
15、
16、
三、解答题
17、（1）当
时，向量与
的夹角为
当
时，向量与的夹角为
（2）对任意、恒成立，即
对任意、恒成立，所以
或
，解得
或
，故所求实数的取值范围是
。
| | 4 | -2 |
|
|
|
|
18、若按方案一，设收益为
万元，则其分布列为
(万元)
若按方案二，设收益为
万元，则其分布列为
|
| 2 | 0 | -1 |
|
|
|
|
|
(万元)
若按方案三，收益
(万元)
，又
，可知
，这说明虽然方案一、二收益相等，但方案二更稳妥，所以建议李师傅家选择方案二投资较合理。
19、（1）椭圆的方程为
（2）设点A、B、M的坐标分别为
，易知点F的坐标为
，将A的坐标代入椭圆方程得
，
同理可得
，则
是方程
的两根，
故
（定值）。
20、（1）连结DM、DN并延长，分别AB、A1B1交于点P、Q，连结PQ，
，
（2）
即为二面角的平面角，到平面的距离为
（3）在平面的射影为。
21、（1）
（2）
，当
即
时，由于，则
，故函数
在
上单调递增，所以
，
由
得
（舍去）；当
即
时，函数在
上递减，在
上递增，所以
，得
综上可知，存在实数，使得当时，的最小值是3.
（3）因为
与
都是偶函数，所以只要证明时，成立即可，证明如下：
当且时，
，
，
设
，
，在
上递减，在
上递增
，则
又
，
当时
，
递减
，而
故当时，
22、（1）
（2）设
，则
，
又
（3）假设存在
满足题设条件，则
，即
，即
由
得
从而
代入上式得
；
猜想
，以下用数学归纳法证明从略。