





成都市2005~2006学年度上期期末调研考试
高一数学试题参考答案及评分意见
一、选择题:(每小题5分,共60分)
1.D; 2.D; 3.B; 4.C; 5.B; 6.B; 7.C; 8.D; 9.D; 10.D; 11.C; 12.D
二、填空题:(每小题5分,共20分)
13.不相等的角不是对顶角,真;
14.{yy≠3,y∈R};
15.![]() .
.
16.{xx>![]() 且x≠1}.
且x≠1}.
17.解:将已知函数化为分段函数,有
 y=
y=
![]() ……3分
……3分
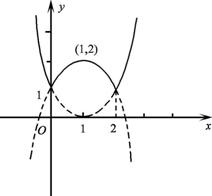
(Ⅰ)当x≤0或x≥2时,其图象是开口向上,以(1,0)为顶点,x=1为对称轴的抛物线的一部份;
(Ⅱ)当0<x<2时,其图象是开口向下,以(1,2)为顶点,x=1为对称轴的抛物线的一部分.
图象如右图实线部分. ……2分
函数的增区间为[0,1],[2,+∞];减区间为![]() ,[1,2].
……4分
,[1,2].
……4分
18.解:∵{an}是等比数列,
∴a2·an-1=a1q·a1qn-2=a1·qn-1=a1·an,
……2分
![]() a1+an=66,
a1+an=66,
∴
a1·an=128. ……2分
![]()
![]() a1=2,
a1=64,
a1=2,
a1=64,
解得 ……①或 ……② ……2分
an=64; an=2.
由①,an=a1qn-1,即64=2qn-1,
∴qn-1=32.显然q≠1.
代入Sn=![]() ,得
,得![]() =126.
=126.
解得q=2,从而n=6. ……3分
由②,得qn-1=![]() ,
,
代入前n项和公式,得
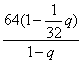 =126.
=126.
解得,q=![]() ,从而n=6.
……3分
,从而n=6.
……3分
∴![]() 或
或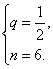 ……1分
……1分
19.解: ……4分
……4分
解这个方程组,得
![]() ……2分
……2分
∴f![]()
![]() ≥
≥![]() .
.
“=”当且仅当![]() 时成立.
……4分
时成立.
……4分
故![]() 的最小值为
的最小值为![]() ,当
,当![]() 时取得.
……1分
时取得.
……1分
20.解:A={x1≤x≤4}. ……1分
记![]() ,其图象是一条开口向上的抛物线.
……1分
,其图象是一条开口向上的抛物线.
……1分
(Ⅰ)若B=![]() ,显然有B
,显然有B![]() A.
A.
此时抛物线与x轴无交点.故![]() <0.
<0.
即![]()
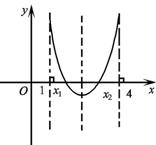 ∴-1<a<2.
……4分
∴-1<a<2.
……4分
(Ⅱ)若B≠![]() ,设抛物线与x轴交点的横坐标为x1、x2,且x1≤x2.要使B
,设抛物线与x轴交点的横坐标为x1、x2,且x1≤x2.要使B![]() A,则应有
A,则应有
1≤x1≤x2≤4.
由右图可知,
当x=1时,y=12-2a·1+a+2≥0.
当x=4时,y=42-2a·4+a+2≥0.
且1≤-![]() ≤4.
≤4.
解得1≤a≤![]() .
……4分
.
……4分
由(Ⅰ)、(Ⅱ),得a的取值范围是-1<a≤![]() .
……2分
.
……2分
21.解:设数列![]() 的公差为d(d≠0),
的公差为d(d≠0),![]() 的公比为q.
的公比为q.
则![]()
![]()
∵![]()
∴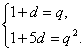 ……2分
……2分
解这个方程,得
![]() (舍去) ……2分
(舍去) ……2分
∴![]()
![]() ……2分
……2分
假设存在常实数a、b,使得![]() N*),
N*),
则 ![]() (n∈N*)
(n∈N*)
∴![]() (n∈N*)
……2分
(n∈N*)
……2分
∵上式对任意的n∈N*都成立,
∴ ……2分
……2分
解这个方程组,得
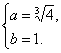 ……1分
……1分
∴存在常实数![]() ,便得对于任意n∈N*都有
,便得对于任意n∈N*都有![]() ……1分
……1分
22.解:(Ⅰ)设![]() 是
是![]() 在(0,+∞)上的不动点,则
在(0,+∞)上的不动点,则
![]() ……2分
……2分
解得 ![]() ,即1是
,即1是![]() 在(0,+∞)上的不动点. ……2分
在(0,+∞)上的不动点. ……2分
(Ⅱ)设![]() 在(0,+∞)有解,
在(0,+∞)有解,
则 ![]() ……①在(0,+∞)上有解.
……2分
……①在(0,+∞)上有解.
……2分
∴![]() ≥
≥![]() ≥
≥![]() ≤
≤![]() ……2分
……2分
当![]() ≥
≥![]() 时,方程①的两根均为负数,不符合(0,+∞)的条件. ……2分
时,方程①的两根均为负数,不符合(0,+∞)的条件. ……2分
当![]() ≤
≤![]() 时,方程①的两根都是正数.
时,方程①的两根都是正数.
故![]() 在(0,+∞)上有不动点
在(0,+∞)上有不动点![]() ≤
≤![]() ……2分
……2分
∴![]() 在(0,+∞)上没有不动点时,
在(0,+∞)上没有不动点时,![]() ……1分
……1分
欢迎访问 http://www.k12zy.com