朝阳区2002——2003年学第二学期高三综合练习(一)
数学(文史类)
2003.4
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至8页。共150分,考试时间120分钟。
第Ⅰ卷(选择题,共50分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用像皮擦干净后,再选涂其它答案,不能答在试题卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
三角函数的和差化积公式
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
![]()
其中c′、c分别表示上、下底面周长,l表示斜高或母线长台体的体积公式
![]()
其中S′、S分别表示上、下底面面积,h表示高
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数![]() 的共轭复数是
的共轭复数是
(A)1+2i(B)![]()
(C)1-2i(D)![]()
(2)若a>b>0,集合![]() ,
,![]() ,则
,则![]() 表示的集合为
表示的集合为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(3)函数f(x)是以π为周期的奇函数,且![]() ,那么
,那么![]() 等于
等于
(A)![]() (B)
(B)![]()
(C)1(D)-1
(4)设a、b、c为三条不同的直线,α、β、γ为三个不同的平面,下面四个命题中真命题的个数是
①若α⊥β,β⊥γ,则α//β。
②若a⊥b,b⊥c,则a//c或a⊥c。
③若![]() ,b、
,b、![]() ,a⊥b,a⊥c,则α⊥β。
,a⊥b,a⊥c,则α⊥β。
④若a⊥α,![]() ,a//b,则α⊥β。
,a//b,则α⊥β。
(A)1个(B)2个
(C)3个(D)4个
(5)已知直线![]() :
:![]() ,
,![]() :
:![]() ,在直角坐标平面上,集合
,在直角坐标平面上,集合![]() 表示
表示
(A)过![]() 和
和![]() 交点的直线集合
交点的直线集合
(B)过![]() 和
和![]() 交点的直线集合,但不包括直线
交点的直线集合,但不包括直线![]()
(C)平行直线![]() 的集合
的集合
(D)平行直线![]() 的集合
的集合
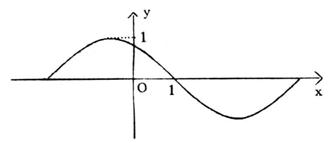
(6)如图是周期为2π的三角函数y=f(x)的图象,那么f(x)可以写成
(A)sin(x-1)
(B)sin(1-x)
(C)sin(-1-x)
(D)sin(1+x)
(7)圆周上有12个不同的点,过其中任意两点作弦,这些弦在圆内的交点个数最多是
(A)![]() (B)
(B)![]()
![]()
(C)![]() (D)
(D)![]()
(8)设椭圆的两焦点分别为(-2,1)、(2,1),两准线间的距离为13,则椭圆的方程是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(9)过点(0,2)的直线l与双曲线c:![]() 的左支交于不同的两点,则直线l的斜率的取值范围是
的左支交于不同的两点,则直线l的斜率的取值范围是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(10)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,则a的值等于()
对称,则a的值等于()
(A)![]() 或
或![]() (B)1或-1
(B)1或-1
(C)1或-2(D)-1或2
第Ⅱ卷(非选择题,共100分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试卷中。
2.答卷前将密封线内的项目填写清楚。
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
(11)已知函数![]() 的定义域为R,值域为
的定义域为R,值域为![]() ,则a的值为________________。
,则a的值为________________。
(12)直线ax+by+1=0被圆![]() 截得的弦长为8,则
截得的弦长为8,则![]() 的值为____________________。
的值为____________________。
(13)要制造一个底面半径为4cm,母线长为6cm的圆锥,用一块长方形材料做它的侧面,这样的长方形的长与宽的最小值分别是_____________。
(14)抽象函数是由特殊的、具体的函数抽象而得到的。如正比例函数![]() ,
,![]() ,
,![]() ,
,![]() 可抽象为
可抽象为![]() 。写出下列抽象函数是由什么特殊函数抽象而成的(填入一个函数即可)。
。写出下列抽象函数是由什么特殊函数抽象而成的(填入一个函数即可)。
| 特殊函数 | 抽象函数 |
|
| |
|
| |
|
| |
|
|
三、解答题:本大题共6小题,共84分。解答应写出文字说明,证明过程或演算步骤。
(15)(本小题满分14分)
已知函数![]()
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)解不等式f(x)<0。
(16)(本小题满分14分)
已知函数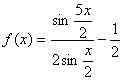
(Ⅰ)将f(x)表示成cosx的整式;
(Ⅱ)若y=f(x)与y=g(x)=a(cosx+1)的图象在(0,π)内至少有一个公共点,试求a的取值范围。
(17)(本小题满分14分)
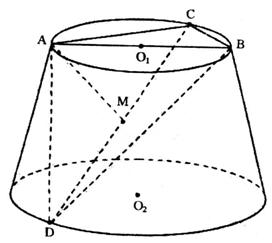
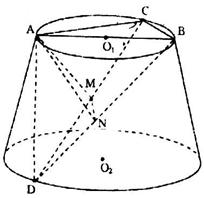
如图,AB是圆台上底面⊙![]() 的直径,C是⊙
的直径,C是⊙![]() 上不同于A、B的一点,D是下底面⊙
上不同于A、B的一点,D是下底面⊙![]() 上的一点,过D、A、C的截面垂直于下底面,M为DC的中点,AC=AD=2,∠DAC=120°,∠BDC=30°。
上的一点,过D、A、C的截面垂直于下底面,M为DC的中点,AC=AD=2,∠DAC=120°,∠BDC=30°。
(Ⅰ)求证:AM⊥平面DBC;
(Ⅱ)求二面角A—DB—C的正切值;
(Ⅲ)求三棱锥D—ABC的体积。
(18)(本小题满分14分)
某加油站需要制造一个容积为![]() 的圆柱形储油罐,已知用来制作底面的铁板每平方米价格为40元,用来制作侧面的铁板每平方米价格为32元,若不计制作损耗。
的圆柱形储油罐,已知用来制作底面的铁板每平方米价格为40元,用来制作侧面的铁板每平方米价格为32元,若不计制作损耗。
(Ⅰ)设储油罐底面半径为x(m),材料成本价为y(元),试用变量x表示y;
(Ⅱ)问储油罐底面半径和高各为多少时,制作的储油罐的材料成本价y最低?
(19)(本小题满分14分)
已知函数![]() 。
。
(Ⅰ)求f(x)的反函数,并指出其定义域;
(Ⅱ)设数列![]()
![]() 的前n项和为
的前n项和为![]() ,若对于所有大于1的自然数n都有
,若对于所有大于1的自然数n都有![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)令![]() ,求:
,求:![]()
(20)(本小题满分14分)
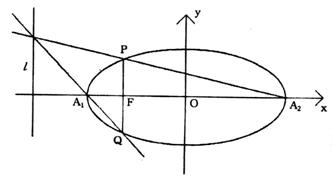
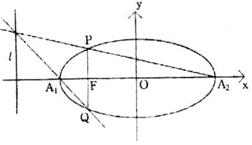
已知:如图,过椭圆c:![]() (a>b>0)的左焦点F(-c,0)作垂直于长轴
(a>b>0)的左焦点F(-c,0)作垂直于长轴![]() 的直线与椭圆c交于P、Q两点,l为左准线。
的直线与椭圆c交于P、Q两点,l为左准线。
(Ⅰ)求证:直线![]() 、
、![]() 、l共点;
、l共点;
(Ⅱ)若过椭圆c左焦点F(-c,0)的直线斜率为k,与椭圆c交于P、Q两点,直线![]() 、
、![]() 、l是否共点,若共点请证明,若不共点请说明理由。
、l是否共点,若共点请证明,若不共点请说明理由。
朝阳区2002——2003学年第二学期高三综合练习(一)
数学(文史类)参考答案及评分标准
2003.4
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | C | C | A | D | B | D | A | D | C |
二、填空题
| 11 | 12 | 13 | 14 |
| a=-1或a=3 |
| 12cm,9cm | 幂函数 指数函数 对数函数 正切函数f(x)=tgx |
三、解答题
15.解:
(I)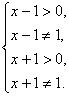 ……………………………………………………2分
……………………………………………………2分
解得:x>1且x≠2。
∴函数f(x)的定义域为{xx>1且x≠2}。…………………………………………4分
(Ⅱ)f(x)<0,即![]() 。
。
(1)当1<x<2时,有0<x-1<1。………………………………………………6分
∴![]() ,
,![]() 。
。
∴原不等式显然成立,解为1<x<2。…………………………8分
(2)当x>2时,有x-1>1。………………………………………………10分
∴![]() ,
,![]() 。
。
∴原不等式变为![]() 。
。
即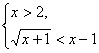
解得x>3 …………………………12分
∴原不等式解集为{x1<x<2或x>3}。………………………………14分
16.(I)解: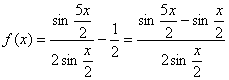 ……………………………………2分
……………………………………2分
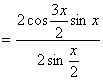 ……………………………………4分
……………………………………4分
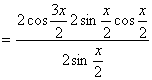 ………………………………………………6分
………………………………………………6分
![]()
![]() ……………………………………8分
……………………………………8分
![]() 。……………………………………10分
。……………………………………10分
(Ⅱ)解:令g(x)=f(x)
a(cosx+1)=(2cosx-1)(cosx+1)。
∵x∈(0,π),
∴cosx+1≠0。
∴a=2cosx-1。………………………………………………12分
∴![]() 。
。
∴-3<a<1。
当-3<a<1时,y=f(x)与y=g(x)的图象在(0,π)内至少有一个公共点。
……………………………………………………14分
17.(I)证明:在△ADC中,AC=AD,M是DC的中点
∴AM⊥DC …………………………2分
∵平面DAC⊥平面ABC,
C为圆![]() 上异于A、B的一点,则有BC⊥AC,
上异于A、B的一点,则有BC⊥AC,
∴BC⊥平面DAC,故BC⊥AM ……………………………………………………4分
∴AM⊥平面DBC。……………………6分
(Ⅱ)解:作MN⊥DB于N,连接AN,由三垂线定理可知AN⊥DB。
即![]() 。
。
数列![]() 是等差数列,公差为
是等差数列,公差为![]() ,
,![]() 。
。
∴![]() 。
。
即![]() 。……………………………………8分
。……………………………………8分
当n≥2时,![]() ,
,
当n=1时,![]() ,满足
,满足![]()
∴![]() 。………………………………10分
。………………………………10分
(Ⅲ)∵![]() ,
,
∴![]() 。
。
………………………………………………12分
∴![]() 。…………………………14分
。…………………………14分
20.解:(I)由方程组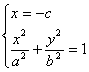
解得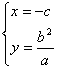 或
或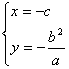
则点![]() ,
,![]() …………………………2分
…………………………2分
直线![]() 的方程为
的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() 。
。
………………………………4分
由方程组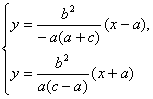
解得![]() 。……………………………………6分
。……………………………………6分
因为左准线l的方程为![]() ,所以直线
,所以直线![]() 与
与![]() 的交点在l上。
的交点在l上。
故直线![]() ,
,![]() ,l相交于一点。……………………8分
,l相交于一点。……………………8分
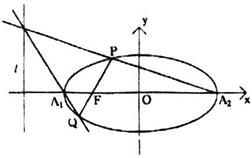
(Ⅱ)设点P、Q的坐标分别为![]() ,
,![]() ,不妨设
,不妨设![]() 。
。
直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,则
,则
![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
直线![]() 的方程为
的方程为![]() 。
。
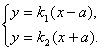
解得交点的横坐标为![]() ,
,
即![]() 。
。
……………………………………10分
直线PQ的方程为y=k(x+c)。
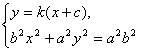 。
。
消去y得![]()
设![]() ,方程(*)的二根为
,方程(*)的二根为![]() ,
,![]() ,
,
由韦达定理得:![]() ,
,![]() 。……………………12分
。……………………12分
∵点P,Q在直线PQ上,
∴![]() ,
,![]() 。
。
∴![]() ,
,
![]() ,其中
,其中![]() ,
,
![]() ,
,
![]() 。
。
∴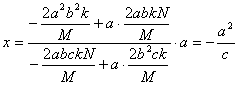 ,
,
因为左准线l的方程为![]() ,所以直线
,所以直线![]() 与
与![]() 的交点在l上。
的交点在l上。
故直线![]() ,
,![]() ,l相交于一点。……………………14分
,l相交于一点。……………………14分