高三第二学期期中练习
数学（文科）
参考公式：
三角函数的积化和差公式
正棱台、圆台的侧面积公式
其中c′、c分别表示上、下底面周长，l表示斜高或母线长
台体的体积公式
其中S′、S分别表示上、下底面积，h表示高
一、选择题：本大题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）函数
的定义域是（ ）
（A）（1，2] （B）（1，2） （C）（2，+∞） （D）（-∞，2）
（2）椭圆
的准线方程为（ ）
（A）
（B）
（C）
（D）
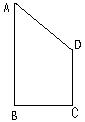
（3）直线梯形ABCD中，AB∥DC，AB=2CD，∠A=45°，AD=2。以直线AB为轴将梯形ABCD旋转一周所得旋转体的体积为（ ）
（A）
（B）
（C）
（D）
（4）已知复数z=1+i，复数
，那么ω的三角形式为（ ）
（A）
（B）
（C）
（D）
（5）已知
，则
的值是（ ）
（A）
（B）
（C）-3 （D）3
（6）已知等比数列
公比为q且q>1，若
，则对于任意自然数n，都有（ ）
（A）
（B）
（C）
（D）
的大小关系与n的值有关
（7）已知a，b是直线，α，β，γ是平面。给出下列命题：①
，则a//b；②
，则α//β；③
，则
；④
则
。其中错误命题的序号是（ ）
（A）① （B）②
（C）③ （D）④
（8）如果直线
与圆
有两个不同的交点，则点P（a，b）与圆的位置关系是（ ）
（A）P在圆外 （B）P在圆上
（C）P在圆内 （D）P与圆的位置关系不确定
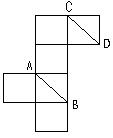
（9）将正方体纸盒展开（如图），直线AB，CD在原正方体中的位置关系是（ ）
（A）平行 （B）垂直
（C）相交且成60°角 （D）异面且成60°角
（10）从7人中选派5人到10个不同交通岗的5个中参加交通协管工作，则不同的选派方法有（ ）
（A）
种
（B）
种
（C）
种
（D）
种
（11）若椭圆的短轴的两个端点与长轴的一个端点是一个正三角形的三个顶点，则椭圆的离心率等于（ ）
（A）
（B）
（C）
（D）
（12）已知
是奇函数，定义域为
。又在区间
上是增函数，且
。如果
，则x的取值范围是（ ）
（A）
（B）（0，1）
（C）
（D）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
（13）若
的展开式中第三项系数为36，则自然数n的值是______________。
（14）集合
且
，则b=________。
（15）在等差数列中，若前9项的和是90，则
的值是______________。
（16）已知函数
。下列命题：①f(x)是偶函数；②f(x)的图象与y轴交点的纵坐标为3；③f(x)在上是增函数；④有最大值4。其中正确命题的序号是____________________。
三、解答题：本大题共6个小题，共74题。解答应写出文字说明、证明过程或演算步骤。
（17）（本小题满分12分）
已知
（Ⅰ）化简f(x)的解析式；
（Ⅱ）若
，求
，使函数f(x)为偶函数。
（18）（本小题满分12分）
解关于x的不等式：
。
（19）（本小题满分12分）
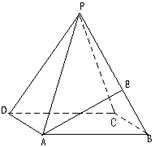
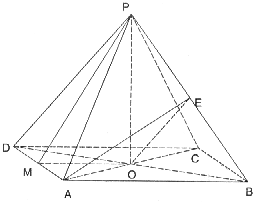
如图所示，正四棱锥P-ABCD中，侧棱PA与底面ABCD所成角的正切值为
。
（Ⅰ）求侧面PAD与底面ABCD所成二面角的大小；
（Ⅱ）项E是PB中点，求异面直线PD与AE所成角的正切值。
（20）（本小题满分12分）
已知函数
。
（Ⅰ）将
的图象向右平移两个单位，得到函数
，求函数的解析式；
（Ⅱ）函数
与函数的图象关于直线
对称，求函数的解析式。
（21）（本小题满分12分）
已知半圆
的直径为OA，O为坐标原点，点P在半圆上，双曲线以O、A为焦点，且过点P。
（Ⅰ）当
时，求双曲线的方程；
（Ⅱ）当
且
时，用双曲线的半实轴长a表示点P的坐标。
（22）（本小题满分14分）
这是一个计算机程序的操作说明：
（1）初始值
；
（2）
（将当前n+1的值赋予新的n）；
（3）
（将当前x+2的值赋予新的x）；
（4）
（将当前2y的值赋予新的y）；
（5）z=z+xy（将当前z+xy的值赋予新的z）；
（6）如果z>7000，则执行语句（7），否则回语句（2）继续进行；
（7）打印n，z；
（8）程序终止。
由语句（7）打印出的数值为__________，_____________。
以下写出计算过程：
高三数学期中练习（文科）参考答案
2002．5
一、选择题（每小题5分，共60分）
（1）B （2）C （3）A （4）D （5）C （6）B （7）B （8）A （9）D （10）D （11）C （12）A
二、填空题（每小题4分，共16分）
（13）9 （14）2 （15）10 （16）②
三、解答题
（17）本小题满分12分
解：（Ⅰ）
………………4分
………………………6分
（或
）…………………………8分
（Ⅱ）当
时，f(x)为偶函数。……………………12分
（18）本小题满分12分
解：原不等式成立的必要条件是
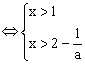………………2分
由a>2且
，故
………………4分
∴原不等式等价于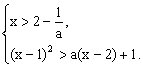
…………………………6分
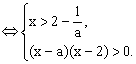……………………………………8分
而a>2，故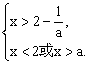
………………………………10分
∴
。
∴不等式的解集是
……………………12分
（19）本小题满分12分
解：（Ⅰ）连结AC，BD交于O，连结PO。
∵P-ABCD为正四棱锥，
∴PO⊥底面ABCD。
作PM⊥AD于M，连结OM，
∴OM⊥AD。
∴∠PMO为侧面PAD与底面ABCD所成二面角的平面角。……………………2分
∵PO⊥底面ABCD，
∴∠PAO为PA与底面ABCD所成的角。……………………3分
∴
。
设AB=a，∴
，
。
∴
。
∴
。……………………………………………………………5分
∴∠PMO=60°即侧面PAD与底面ABCD所成二面角为60°……………………6分
（Ⅱ）连结EO，∵E为PB的中点，O为BD的中点，∴EO//PD。
∴∠AEO为异面直线AE与PD所成角。……………………………………………8分
在Rt△PAO中，，
，∴
。………………………9分
∴ 
，由AO⊥截面PDB，可知AO⊥EO。
在Rt△AOE中
。
即异面直线AE与PD所成角的正切值是
。……………………12分
（20）本小题满分12分
解：（Ⅰ）
。……………………………4分
（Ⅱ）设y=h(x)图象上一点P（x，y），
点P关于y=1的对称点为Q（x，2-y），………………………………6分
由点Q在y=g(x)的图象上，∴
，……………………9分
于是
，即
。…………………12分
（21）本小题满分12分
解：（Ⅰ）双曲线中心，（1，0），半焦距c=1，…………………………1分
设所求双曲线的方程为
。
∵点
在双曲线上，∴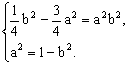
……………………4分
解方程组，可得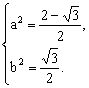
……………………………………………6分
即所求双曲线的方程为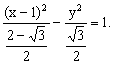
………………………………7分
（Ⅱ）设点P的坐标为（x，y），又点P是双曲线与圆的公共点，所以
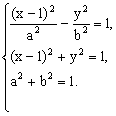消
，得
。……………………10分
∵y>0， ∴
。
∵， ∴x<1。 ∴
。………………12分
（22）本小题满分14分
解：设n=i时，x，y，z的值分别为
，
，
。
依题意，
，
。∴
是等差数列，且
……………2分
，
，∴
是等比数列，且
………………………………4分
，
。……………………………………………………………5分
∴
∴
以上两式相减，得
………………10分
依题意，程序终止时：
，
，
即
可求得n=8，z=7682。……………………………………14分
说明：其它正确解法按相步骤给分。