山东济宁02-03年高三数学质量模拟(一)
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试用时120分钟。
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）函数y=lgx的反函数与y=lg
的反函数的图象关于
（A）x轴对称 （B）y轴对称 （C）直线y=x对称 （D）原点对称
（2）与向量
=（1，-
）平行的单位向量是
（A）（1，-） （B）（，1） （C）（
，-
） （D）（-，）
（3）若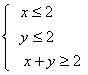
，则目标函数u=x-2y的最大值是
（A）-4 （B）-2 （C）2 （D）4
（4）设x、y∈R，命题p：│x-y│＜1，命题q：│x│＜│y│+1，则p是q成立的
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
（5）已知集合M={x -1＜x＜2＝，N=
，则M∩N为
（A）{a -1≤a＜2} （B）{a -1＜a＜2}
（C）{a -1＜a＜1＝ （D）{a -1＜a≤1＝
（6）式子C3n – C4n +C5n - …+（-1）n-1Cnn （n≥3且n∈N*）
（A）恒为正 （B）恒为零 （C）恒为负 （D）可正可负
（7）设有直线m、n和平面α、β，则在下列命题中，正确的是
（A）若m∥n，m⊥α，n⊥β，则α⊥β （B）若m∥n，m⊥β，m
α，则α⊥β
（C）若m⊥n，m⊥α，nβ，则α∥β （D）若m∥n，mα，nβ，则α∥β
（8）△ABC是sinB·sinC=cos2
，则△ABC的形状为
（A）直角三角形 （B）等边三角形 （C）等腰三角形 （D）等腰直角三角形
（9）抛物线y=4x2-x的焦点到准线的距离是
（A）2 （B）4
（C）
（D）
（10）已知f（x）=x2+x+c，若f（0）＞0，f（p）＜0，则
（A）f（p+1）＞0 （B）f（p+1）＜0 （C）f（p+1）=0 （D）f（p+1）的符号不确定
（11）从高中三年级8个班中抽出10名同学，组成年级篮球队，要求每个班至少出一名同学，则不同的组成方式有
（A）8种 （B）28种 （C）36种 （D）45种
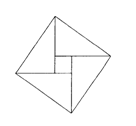
（12）2002年初月，在北京召开了国际数学家大会，大会会标如图所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是1，小正方形的面积是
，则sin2θ-cos2θ的值等于
（A）1
（B）
（C）
（D）-
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
（13）已知等差数列{an}中，a4+ a7+ a10=18， a6+ a8+ a10=27，若 ak=21，则k=
（14）设P为双曲线
-y2=1上一动点，O为坐标原点，M为线段OP的中点，则点M的轨迹方程是
。
（15）球面内接三棱锥P-ABC，PA⊥平面ABC，PA=2，△ABC是边长为的正三角形，则球面面积为
。
（16）已知函数f（x）=│lgx│，若
＞b＞1，则f（a）、f（b）、f（c）的大小关系为 。
三、解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
（17）（本小题满分12分）
已知函数y=sin2x+2sinxcosx+3cos2x，x∈R，
问：（Ⅰ）函数的最小正周期是多少？
（Ⅱ）函数的最大值与最小值分别是多少？对应的x值分别是什么？
（18）（本小题满分12分）
有A、B两个箱子，A箱中有6张相同的卡片，其中一张写有0，两张写有1，三张写有2；B箱中有7张相同的卡片，其中四张写有0，一张写有1，两张写有2，现从A箱中任取1张，从B箱中任取2张，共3张卡片。
求：（Ⅰ）3张卡片都写有0的概率；
（Ⅱ）3张卡片中数字之积为0的概率。
（19）（本小题满分12分）
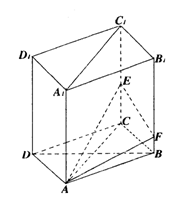已知直四棱柱ABCD-A1B1C1D1的底面是菱形，对角线AC=2，BD=2，E、F分别为棱CC1、BB1上的点，且满足EC=BC=2FB.
（Ⅰ）求证：平面AEF⊥平面A1ACC1；
（Ⅱ）求异面直线EF、A1C1所成角的余弦值。
（20）（本小题满分12分）
甲、乙两企业，2002年的销假量均为p（2002年为第1年），根据市场分析和预测，甲企业前n年的总销售量为
（n2-n+2），乙企业第n年的销售量比前一年的销售量不足另一企业年销售量的20%，则该企业被另一企业兼产。经计算2011年之前，不会出现兼并局面，试问2012年是否会出现兼并局面，并写出判断过程。
（21）（本小题满分12分）
设f（x）=
（Ⅰ）求f（x）的值域；
（Ⅱ）判断F（x）=lgf（x）在[ -1，1 ]上的单调性，并说明理由；
（Ⅲ）（文科学生不做）求证：lg
≤F（│t-
│-│t+│）≤lg
（t∈R）.
（22）（本小题满分14分）
已知点A（1，1）是椭圆
=1（a＞b＞0）上一点，F1、F2是椭圆的两焦点，且满足│AF1│+│AF2│=4.
（Ⅰ）求椭圆的两焦点坐标；
（Ⅱ）设点B是椭圆上任意一点，如果│AB│最大时，求证A、B两点关于原点O不对称；
（Ⅲ）（文科学生不做）设点C、D是椭圆上两点，直线AC、AD的倾斜角互补，试判断直线CD的斜率是否为定值？