山东昌邑一中02-03年上学期高二数学期末考试

山东昌邑一中02-03年上学期高二数学期末考试

说明：本套试题分Ⅰ、Ⅱ卷，第Ⅰ卷60分，第Ⅱ卷90分，共150分，时间120分钟。

第Ⅰ卷 （选择题　共60分）

一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）直线3x-4y+5=0关于y轴对称的直线的方程为（　　　 ）

（A）3x+4y-5=0　　　　  （B）3x+4y+5=0

（C）-3x+4y-5=0　　　　 （D）-3x+4y+5=0

（2）双曲线=1的两条准线的距离等于（　　　 ）

（A）　　　　　　 （B）　　　 （C）　　  （D）

（3）若直线Ax+By+C=0通过第二、三、四象限，则系数A、B、C需满足的条件是（　）

（A）A、B、C同号　　　　 （B）AC＜0且BC＜0

（C）C=0且AB＜0　　　　 （D）A=0且BC＜0

（4）方程（x-y）²+(xy-1)²=0的曲线是（　　　　）

（A）一条直线和双曲线　　　　 （B）一条直线或双曲线

（C）双曲线　　　　　　　　　 （D）两个点

（5）已知直线x=a（a＞0）和圆（x-1）²+y²=4相切，那么a的值是（　　　）

（A）5　　 （B）4　　　 （C）3　　　（D）2

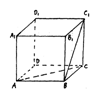
（6）如图所示，正方体ABCD—A₁B₁C₁D₁中，直线BC₁和AC

（A）相次且垂直　　（B）相次但不垂直

（C）异面且垂直　　（D）异面但不垂直

（7）若P（3cosα，3sinα，1），Q（2cosθ,2sinθ,1），则││的取值范围是（　　）

（A）[ 0，5 ]　　　 （B）[ 0，25 ]　　 （C）[ 1，5 ]　　　（D）[ 1，25 ]

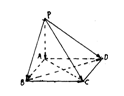（8）如图所示，四边形ABCD为矩形，PA⊥平面ABCD，则下列各组向量中，数量积不为零的是（　　 ）

（A）与　　  （B）与

（C）与　　  （D）与

（9）a，b为异而直线，aα，bβ，α∩β=m必定（　　　　）

（A）与a、b都相交　　　　  （B）至少与a、b中的一条相交

（C）与a、b都不相交　　　　（D）至多与a、b中的一条相交

（10）已知直线l⊥平面α，直线m_{平面β，有下面四个命题：}

_{①α∥β1⊥m　　②α⊥β1∥m　　③1∥mα⊥β　　④1⊥mα∥β}

_{其中正确的两个命题是（　　　）}

_{（A）①与②　　（B）③与④　 （C）②与④　　 （D）①与③}

_{（11）平面直角坐标系中，O为坐标原点，已知两点A（2，0），B（0，1），若点C满足}

_{=sinα+cosα，其中α∈R，则点C的轨迹方程为（　　　 ）}

_{（A）x-2y+2=0　 （B）　 （C）x2+y2=4　　（B）}

（12）设坐标原点为O，抛物线y²=2x与过焦点的直线交于A、B两点，则=（　　）

（A）　　　 （B）-　　　　 （C）3　　　 （D）-3

第Ⅱ卷（非选择题　　共90分）

二、填空题：本大题共4小题，每小题4分，共16分。把答案填写在题横线上。

（13）椭圆=1的离心率为　　　　　　　　　　　　　 。

（14）已知点A（-1，0），B（1，0），C（0，1），若点P在线段AB上移动，则直线PC的倾斜角的范围是　　　　　　　　　  。

（15）双曲线9y²-16x²=144的渐近线方程为　　　　　　　　　　　  。

（16）已知空间四边形OABC，点M、N分别是OA、BC的中点，且。若用、、表示向量，则=　　　　　　　　　　  。

三、计算题：本大题6小题，满分74分，解答应写出文字说明、证明过程或演算步骤。

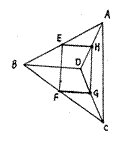（17）（满分12分）

如图所示，在空间四边形ABCD中，E、F、G、H分别是边

AB、BC、CD、DA的中点，且AC⊥BD，求证四边形EFGH是矩形。

（18）（满分12分）

已知双曲线的焦点在y轴上，并且双曲线上两点P₁、P₂的坐标分别为（3，-4）、（，5），求双曲线的标准方程。

（19）（满分12分）

过P（2，1）作直线l，分别交x轴、y轴的正半轴于A、B两点，求使取得最大值时的直线l的方程。

（20）（满分12分）

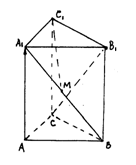直角△ABC中，CA=CB=1，∠ACB=90°，几何体ACB—A₁B₁C₁是由水平放置的△ABC自下向上平移向量到A₁C₁B₁的轨迹所形成的。如图所示，││=2，M是A₁B的中点。

（Ⅰ）求cos＜＞的值；

（Ⅱ）证明A₁B与C₁M不垂直。

（21）（满分12分）

过抛物线C₁：y²=2px(p＞0)的顶点任作互相垂直的两弦OA与OB。

（Ⅰ）求证A、B两点的纵坐标之积是定值；

（Ⅱ）求证A、B两点连线的中点M的轨迹（记作C₂）仍是一条抛物线；

（Ⅲ）已知定点C（3p,），若（Ⅱ）中抛物线C₂的焦点为F，并且动点N在C₂上移动，试求当│NC│+│NF│最小时N点的坐标。

（22）（满分14分）

某人上午7时乘船，以V海里/时（4≤V≤20）的速度从A港出发向距离A港50海里的B港匀速行驶，到达后，又乘汽车以W千米/时（30≤W≤100）的速度自B港向距离B港300千米的C市匀速驶去，并要求同一天下午4至9点到达C市。设乘汽车与船所需的时间分别是x、y小时。

（Ⅰ）画出满足上述条件的x、y的可行域；

（Ⅱ）如果已知所需的经费P=100+3·（5-x）+2·（8-y）元，那么V、W分别是多少时走得最经济？此时需花费多少元？