北京市西城区2002年抽样测试
![]() 高三数学试卷(文科)
高三数学试卷(文科)
(2002.6)
参考公式:
三角函数的和差化积公式
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
![]()
其中c',c分别表示上、下底面周长,l表示斜高或母线长。
一、选择题:本大题共12小题;每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合要求的。每小题选出答案后,用铅笔在下表中将对应答案标号涂黑。
1.![]() 的值是( ).
的值是( ).
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
2.下列函数中没有反函数的是( )
A.y=2x B. ![]()
C. ![]() D.
D.![]()
3.设![]()
![]() 则( ).
则( ).
A. Q=P
B. ![]()
C. ![]()
D. P∩Q={(2,4)}
4.过原点且与圆![]() 截得的弦长为
截得的弦长为![]() 的一条直线的方程是( ).
的一条直线的方程是( ).
A.
y=x B. ![]()
C.
y=-x D. ![]() x
x
5.双曲线![]() 的一个焦点到一条渐近线的距离等于( ).
的一个焦点到一条渐近线的距离等于( ).
A. ![]() B.3
B.3
C. 4 D. 2
6.在△ABC中,sinA: sinB:sinC=3:2:4,则cosC的值为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.某企业2001年12月份的产值是这年1月份产值的p倍,则该企业2001年年度产值的月平均增长率为( )。
A. ![]() B.
B.![]()
C.![]() D.
D.![]()
8.学校要选派4名爱好摄影的同学中的3名分别参加校外摄影小组的3期培训(每期只派1名),由于时间上的冲突,甲、乙两位同学都不能参加第1期培训,则不同的选派方式有( )。
A. 6种 B. 8种
C. 10种 D. 12种
9.一圆锥被平行于底面的截面截成一个小圆锥和一个圆台,若小圆锥的体积为y,圆台的体积为x,则y关于x的函数图象的大致形状为( ).
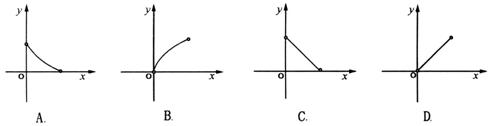
10.直平行六面体![]() 的棱长均为2,∠BAD=60°,则对角线
的棱长均为2,∠BAD=60°,则对角线![]() 与侧面
与侧面![]() 所成角的正弦值为( )。
所成角的正弦值为( )。
A.![]() B.
B. ![]()
C. ![]() D.
D.![]()
11. 设![]() 的展开式中,奇数项的二项式系数之和为
的展开式中,奇数项的二项式系数之和为![]() ,数列
,数列![]() 的前n项和记为
的前n项和记为![]() ,则
,则![]() = ( ).
= ( ).
A.
0 B.![]()
C. 1 D.2
12. 已知直线m,n及平面∝,其中m//n,那么在平面∝内到两条直线m,n距离相等的点的集合可能是: ①一条直线;②一个平面;③一个点;④空集,其中正确的是( )
A.①②③ B.①②④
C.①④ D.②④
二. 填空题:本大题共4小题;每小题4分,共16分。把答案填在题中横线上。
13.抛物线 ![]() 的焦点坐标是_________________.
的焦点坐标是_________________.
14.已知圆台的母线与底面成30°角,轴截面面积为S,则圆台的侧面积为_______.
15.在各项都是正数的等比数列![]() 中,公比q ≠1,并且
中,公比q ≠1,并且
![]() ,
,![]() ,
,![]() 成等差数列,则公比q的值为__________.
成等差数列,则公比q的值为__________.
16.设有两个命题:
(1)不等式x+x-1>m的解集是R;
(2)函数 ![]() 是减函数.如果这两个命题中有且只有一个真命题,则实数m的取值范围是__________.
是减函数.如果这两个命题中有且只有一个真命题,则实数m的取值范围是__________.
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
已知z∈C,![]()
(Ⅰ)求z的最小值;
(Ⅱ)若![]() ,求z.
,求z.
18.(本小题满分12分)
如图α-ι-β是120°的二面角,A,B两点在棱上,AB=2,D在α内,三角形ABD是等腰直角三角形,∠DAB=90°,C在β内,三角形ABC是等腰直角三角形,∠ACB=90°,
∠ABC=60°.
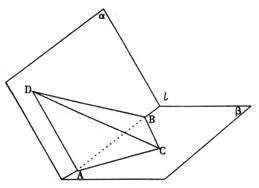
(Ⅰ)求三棱锥D-ABC的体积;
(Ⅱ)求直线BD与平面β所成的角的正弦值;
(Ⅲ)求二面角D-AC-B的平面角的正切值.
19. (本小题满分12分)
解关于x的不等式:![]() (a∈R).
(a∈R).
20.(本小题满分12分)
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足:
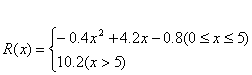
假定该产品产销平衡,那么根据上述统计规律.
(Ⅰ)要使工厂有赢利,产量x应控制在什么范围?
(Ⅱ)工厂生产多少台产品时,可使赢利最多?
(Ⅲ)求赢利最多时每台产品的售价.
21.(本小题满分13分)
已知椭圆的中心在原点,焦点在x轴上,过它的右焦点![]() 引倾斜角为
引倾斜角为![]() 的直线l交椭圆于M,N两点,若M,N两点到椭圆右准线的距离之和为
的直线l交椭圆于M,N两点,若M,N两点到椭圆右准线的距离之和为![]() ,椭圆左焦点
,椭圆左焦点![]() 到直线l的距离为
到直线l的距离为![]() ,求椭圆的方程.
,求椭圆的方程.
22. (本小题满分13分)
已知数列{![]() }各项均为正数,
}各项均为正数,![]() 为其前n项的和,并且对于n∈N都有
为其前n项的和,并且对于n∈N都有![]() ,
,![]() ,
,![]() 成等差数列。
成等差数列。
(Ⅰ)求数列{![]() }的通项
}的通项![]() ;
;
(Ⅱ) 试比较![]() 与
与![]() 的大小.
的大小.
高三数学(文科)参考答案及评分标准
2002.6
一、 CBBDC ADDCD BB
二、(13) (![]() ) (14)2πS (15)
) (14)2πS (15)![]() (16) 1≤m<2
(16) 1≤m<2
三、解答题:其他解法仿此给分
17.解:(Ⅰ)设z=a+bi (a、b∈R)
由已知得![]()
∴![]() ,
,
∴a-b=1 即a=b+1--------①,---------------3分
∵![]()
![]() 又b∈R
又b∈R
∴当![]() 时,z的最小值为
时,z的最小值为![]() . -----------6分
. -----------6分
(Ⅱ)∵![]()
∴![]() 且a>0------------9分
且a>0------------9分
与①式联立,解得![]() ,
,![]() 。
。
即![]() .-----------------------12分
.-----------------------12分
18解:(Ⅰ)过D向平面β做垂线,垂足为O,连结OA并延长至E.
∵AB⊥AD,OA为DA在平面β上的射影,
∴AB⊥OA,
∴∠DAE为二面角α-ι-β的平面角.
∴∠DAE=120°,∴∠DAO=60°.---------2分
∵AD=AB=2,∴![]() .
.
∵△ABC是有一个锐角为30°的直角三角形,斜边AB=2.
∴![]()
又D到平面β的距离![]() .
.
∴![]() -----------------4分
-----------------4分
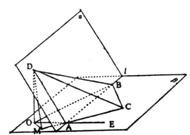
(Ⅱ)由(I)OB为BD在平面β上的射影,
∴∠DBO为直线BD与平面β所成的角,------------------------6分
∴![]() .----------------------------------------------8分
.----------------------------------------------8分
(Ⅲ)过O在β内OM⊥AC,交AC的反向延长线于M,连结DM.
则AC⊥DM.
∴∠DMO为二面角D-AC-B的平面角. --------------------------10分
又在△DOA中,OA=2cos60°=1.
即∠OAM=∠EOC=60°,∴![]() ,
,
∴![]() --------------------------------------------12分
--------------------------------------------12分
19.解:原不等式等价于不等式组:
 --------------------------------------2分
--------------------------------------2分
即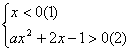 -------------------------------3分
-------------------------------3分
①当a=0时,无解.-------------------------------------------4分
∵不等式(2)中△=4+4a,于是
②当a<-1时,不等式(2)无解,∴原不等式无解.----------------------------6分
③当-1≤a<0时,设![]() 的两根为
的两根为![]() 、
、![]() ,
,
则![]() ∴
∴![]() 、
、![]() 均为正数,
均为正数,
∴不等式(2)的解集是![]() 的子集,∴原不等式无解.----------------------------8分
的子集,∴原不等式无解.----------------------------8分
④当a>0时,不等式(2)的解集为![]() 或
或![]()
∵![]()
![]()
∴原不等式解集为![]() -----------------------------------------11分
-----------------------------------------11分
综上,当a≤0时,原不等式无解;
当a>0时,原不等式的解集为![]() .------------------------12分
.------------------------12分
20.解:依题意,G(x)=x+2. 设利润函数为f(x),则
 ---------------------2分
---------------------2分
(Ⅰ)要使工厂有赢利,即解不等式f(x)>0,
当0≤x≤5时,解不等式![]() .
.
即![]() ,∴1<x<7,
,∴1<x<7,
∴1<x≤5.-------------------------------------------4分
当x>5时,解不等式8.2-x>0,得x<8.2.
∴5<x<8.2 .----------------------------------5分
综上,要使工厂赢利,x应满足1<x<8.2,即产品应控制在大于100台,小于820台的范围内。--------------------------------------------------------------------6分
(Ⅱ)0≤x≤5时,![]() ,
,
故当x=4时,f(x)有最大值3.6.---------------------------------------8分
而当x>5时,f(x)<8.2-5=3.2.
所以,当工厂生产400台产品时,赢利最多。-----------------------------10分
(Ⅲ)即求x=4时的每台产品的售价
此时售价为![]() (万元/百台)=240元/台----------------------------12分
(万元/百台)=240元/台----------------------------12分
21.解:设所求的椭圆方程为![]() ,
,![]() ,
, ![]()
则直线l的方程为y=x-c.---------------------------------------------------------2分
∵![]() 到直线l的距离为
到直线l的距离为![]() ,
,
∴![]() ∴ c=1.-------------------------------------------------------4分
∴ c=1.-------------------------------------------------------4分
∴l:y=x-1,------------------------------------------------------------------------------5分
设M(![]() ),N(
),N(![]() ).
).
则M、N到椭圆右准线的距离之和为![]()
∴![]() ------------①-----------------7分
------------①-----------------7分
由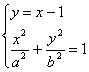 消y得
消y得![]() --------②------9分
--------②------9分
∵a>c,∴a>1,
∴![]() 并且
并且![]() ,
,
∴![]() 代入①整理得:
代入①整理得:
![]() ------------------------------------------------------11分
------------------------------------------------------11分
解得![]() 或
或![]() (舍). ∵a>c, ∴
(舍). ∵a>c, ∴![]() ------------12分
------------12分
∴所求的椭圆方程为![]() ----------------------------------13分
----------------------------------13分
22.解:(I)由已知n∈N时,![]() 总成立.
总成立.
∴![]()
两式作差,得![]() ---------------------------2分
---------------------------2分
∴![]() ∵
∵![]() 、
、![]() 均为正数
均为正数
∴![]() ∴
∴![]() 是公差为1的等差数列-.----------4分
是公差为1的等差数列-.----------4分
又∵n=1时,![]() ,得
,得![]()
∴![]() -----------------------------------5分
-----------------------------------5分
(Ⅱ)即比较![]() 与
与![]() 的大小.
的大小.
当n=1时,前式值为1,后式值为1.∴两式相等.-------------------6分
当n=2时,前式值为![]() ,后式值为
,后式值为![]() ,前式大于后式.
,前式大于后式.
-----------------------------------------------------------------------------------7分
当n=3时,前式值为![]() ,后式值为
,后式值为![]() ,---------8分
,---------8分
前式大于后式.
于是,推测当n≥2时,前式大于后式---------------------------------------9分
假设n=k时(k≥2),猜测成立,即![]() ,--------10分
,--------10分
则当n=k+1时,
![]()
而![]()
![]() -----------12分
-----------12分
∴当n≥2时,前式大于后式.
∴当n=1时,两式相等;当n≥2时,前式大于后式.----------------------13分