西安中学高2002级五月份模拟试题
参考公式:
三角函数的积化和差公式
![]()
![]()
![]()
![]()
正棱台、圆台的侧面积公式
![]() ;其中c',c分别表示上、下底面周长,l表示斜高或母线长。
;其中c',c分别表示上、下底面周长,l表示斜高或母线长。
台体的体积公式
![]() ,其中S',S分别表示上、下底面面积,h表示高。
,其中S',S分别表示上、下底面面积,h表示高。
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一个是符合题目要求的。
1.若使集合![]() 中有且只有一个元素的所有a的组成的集合N,则( )。
中有且只有一个元素的所有a的组成的集合N,则( )。
A.N={-1,1} B.N={0,1}
C.N={-1,0,1} D.N={0,-1}
2.若![]() ,则下列不等式恒成立的是( )。
,则下列不等式恒成立的是( )。
A.sinα<sin2α B.cosα>cos2α
C.tgα<tg2α D.ctgα>ctg2α
3.正三棱柱![]() 中,
中,![]() ,D为AB中点,
,D为AB中点,![]() ,则点
,则点![]() 到平面
到平面![]() 的距离和
的距离和![]() 与
与![]() 所成的角分别为( )。
所成的角分别为( )。

A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.(理)在极坐标系下,两圆ρ=sinθ与ρ=1的位置关系是( )。
A.相交 B.内含
C.外切 D.内切
(文)已知抛物线![]() 与抛物线
与抛物线![]() 关于直线y=-x对称,则
关于直线y=-x对称,则![]() 的准线方程是( )。
的准线方程是( )。
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.若![]() 成等差数列,
成等差数列,![]() 成等比数列,若
成等比数列,若![]() 关于直线l对称,则直线l的方程为( )。
关于直线l对称,则直线l的方程为( )。
A.x+y-7=0 B.y-x+1=0
C.x-y+1=0 D.2x-y-5=0
6.下列判断正确的是( )。
A.![]() 是奇函数
B.
是奇函数
B.![]() 是偶函数
是偶函数
C.![]() 是奇函数 D.f(x)=1既是奇函数又是偶函数
是奇函数 D.f(x)=1既是奇函数又是偶函数
7.(理)设函数![]() 的最大值为α,最小值为β,则sin(β-α)的值等于( )。
的最大值为α,最小值为β,则sin(β-α)的值等于( )。
A.![]() B.
B.![]()
C.0
D.![]()
(文)使![]() 成立的x的一个变化区间是( )。
成立的x的一个变化区间是( )。
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.无穷等比数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() ( )。
( )。
A.![]() B.2 C.4
D.8
B.2 C.4
D.8
9.函数![]() 在[m,n]上是增函数,且f(m)= -A,f(n)=A,则函数
在[m,n]上是增函数,且f(m)= -A,f(n)=A,则函数![]() 在[m,n]上( )。
在[m,n]上( )。
A.是增函数 B.是减函数
C.最大值为A D.最小值为-A
10.已知定义在R上的函数y=f(x)满足下列条件:①对x∈R,都有f(x+4)=f(x);②对任意的![]() ,都有
,都有![]() ;③y=f(x+2)的图象关于y轴对称。则下列结论中,正确的是( )。
;③y=f(x+2)的图象关于y轴对称。则下列结论中,正确的是( )。
A.f(4.5)<f(6.5)<f(7) B.f(4.5)<f(7)<f(6.5)
C.f(7)<f(4.5)<f(6.5) D.f(7)<f(6.5)<f(4.5)
11.已知一正方体内接于一球面,用一个平面去截这个球和正方体,得到的截面图形是一个圆及其内接正三角形,若此正三角形的边长为a,则这个球的外切正方体的表面积为( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.函数![]() 的图象如右图,则( )。
的图象如右图,则( )。
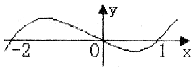
A.a>b>0,c>0 B.a=b<0,c>0
C.a=b>0,c<0 D.a<0,b<0,c<0
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13.设函数![]() 的反函数为
的反函数为![]() ,则函数
,则函数![]() 的定义域为__________________________。
的定义域为__________________________。
14.已知![]() ,
,![]() ,则
,则![]() 的值为______________。
的值为______________。
15.某化工厂生产实验中需依次投放2种化工原料。现已知有5种原料可用,但甲、乙两种原料不能同时使用,且依次投料时,若使用甲原料,则甲必须先投放,共有不同的实验方案_______________种。
16.关于复数![]() ,下列命题:
,下列命题:
①复数![]() 的辐角主值是α。
的辐角主值是α。
②复数z在复平面上对应点的轨迹是单位圆。
③![]() 一定是实数。
一定是实数。
④将复数z在复平面内对应的向量![]() 按顺时针方向旋转90°得向量
按顺时针方向旋转90°得向量![]() ,则点Q对应的复数为
,则点Q对应的复数为![]() 。
。
其中正确命题的序号是__________________。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本题12分) 已知z是虚数,![]() ,求argz的范围。
,求argz的范围。
18.(本题12分) 如图,正三棱柱![]() 的所有棱长均为2,D是BC上一点,
的所有棱长均为2,D是BC上一点,![]() 。
。
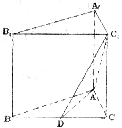
(1)求证:截面![]() ;
;
(2)求二面角![]() 的大小的正弦植;
的大小的正弦植;
(3)求![]() 与截面
与截面![]() 的距离。
的距离。
19.(本题12分)在数列![]() 中,
中,![]() ,且
,且![]() 。
。
(1) 求![]() ;写出数列
;写出数列![]() 的通项公式,并加以证明。
的通项公式,并加以证明。
(2) (理)设 ,令
,令![]() ,求
,求![]() 。
。
(文)设![]() ,令
,令![]() ,
,![]() 。
。
20.(本题12分)某企业实行裁员增效,已知现有员工a人,每人每年可创纯利润1万元,据评估在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元的生活费,并且企业正常运转所需人数不得少于现有员工的![]() ,设该企业裁员x人后年纯收益为y万元。
,设该企业裁员x人后年纯收益为y万元。
(1)写出y关于x的函数关系式,并指出x的取值范围;
(2)当![]() 时,问该企业应裁员多少人,才能获得最大的经济效益(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)。
时,问该企业应裁员多少人,才能获得最大的经济效益(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)。
21.(本题13分)如图,已知双曲线C的对称轴是坐标轴,离心率为![]() ,点
,点![]() 是双曲线C的渐近线
是双曲线C的渐近线![]() 上的两点,
上的两点,![]() 的面积为9,点P是双曲线C上的一点,且点P分有向线段
的面积为9,点P是双曲线C上的一点,且点P分有向线段![]() 所成的比是2。
所成的比是2。
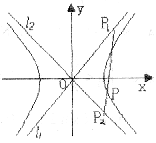
(1)求双曲线C的渐近线方程:
(2)求双曲线C的方程。
22.(本题13分)
(理)定义在区间(-1,1)上的函数f(x)满足:
①对任意![]() ,都有
,都有![]() ;②当
;②当![]() 时,f(x)>0。
时,f(x)>0。
(1)求证f(x)为奇函数; (2)试解不等式![]() 。
。
(文)设函数![]()
(1)当a=2时,求函数f(x)的最小值;
(2)当0<a<1时,判断函数f(x)的单调性,并求出f(x)的最小值。
参考答案:
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B卷答案 | C | B | B | 理D 文C | A | C | 理B 文C | D | D | B | A | C |
二、填空题(每小题4分,共16分)
13.![]()
14. -3
15. 15
16. ③④
三、解答题(共74分)
17.解:设z=x+yi(x, y∈R,且y≠0),……………………………………………1分
则由![]() ,…………4分
,…………4分
得![]() ∵y≠0,由2y(x-1)=0得x=1。…………………………6分
∵y≠0,由2y(x-1)=0得x=1。…………………………6分
把x=1代入到![]() 得
得![]() ,即
,即![]() 。…………8分
。…………8分
从而z=x+yi=1+yi ![]() ,…………………………………10分
,…………………………………10分
∴![]() 。……………………………………………………12分
。……………………………………………………12分
18.解(1)∵![]() ,
,![]() ,∴
,∴![]() ,…………2分
,…………2分
又![]() 。∴
。∴![]() 。
。
又![]() ,∴截面
,∴截面![]() 。………………………4分
。………………………4分
(2)做![]() 于E,则
于E,则![]() ,做
,做![]() 于F,连结CF,则
于F,连结CF,则![]() 。
。
∴∠CFE为二面角![]() 的平面角。……………………………………6分
的平面角。……………………………………6分
在![]() 中,易求得
中,易求得![]() ,在
,在![]() 中,可求得
中,可求得![]() 。
。
故在![]() 中,
中,![]() 。
。
即二面角![]() 大小的正弦值为
大小的正弦值为![]() 。……………………………………8分
。……………………………………8分
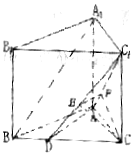
(3)连接![]() 与
与![]() 交于H,在
交于H,在![]() 中易证
中易证![]() ,∴
,∴![]() 。所求距离即为点B到平面
。所求距离即为点B到平面![]() 的距离,…………………………………………………10分
的距离,…………………………………………………10分
由![]() 可求得点B到平面
可求得点B到平面![]() 的距离为
的距离为![]() 。……………………12分
。……………………12分
19.解:(1)![]() ,…………………………………………………………2分
,…………………………………………………………2分
推测![]() 。…………………………………………………………………………4分
。…………………………………………………………………………4分
证明:①当n=1时,由![]() 得
得![]() ,结论正确。
,结论正确。
②假设当n=k(k∈N)时,结论正确,即![]() 。
。
那么当n=k+1时,
![]()
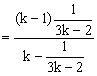
![]()
![]()
![]()
这说明当n=k+1时,结论也正确。
由①、②得,对于![]() 都有
都有![]() 。……………………………………6分
。……………………………………6分
(2)![]() ,…………………………8分
,…………………………8分
∴![]()
![]()
![]() ……………………………………………………………………10分
……………………………………………………………………10分
∴![]() 。………………………………………………………………………12分
。………………………………………………………………………12分
(文)![]()
![]() ………………………………………………………………8分
………………………………………………………………8分
∴![]()
![]() ……………………………………………………………………………10分
……………………………………………………………………………10分
∴![]() …………………………………………………………12分
…………………………………………………………12分
20.解:(1)由题意可得y=(a-x)(1+0.01x)-0.4x,
![]() ……………………………………………………………4分
……………………………………………………………4分
∵![]() ,∴
,∴![]() 。即x的取值范围是
。即x的取值范围是![]() 中的自然数。………………6分
中的自然数。………………6分
(2)∵![]() ,且
,且![]() ,………8分
,………8分
∴![]() 。
。
∴当a为偶数时,![]() 时,y取最大值。……………………………………10分
时,y取最大值。……………………………………10分
当a为奇数时,![]() 时,y取最大值。(∵尽可能少裁人,∴舍去
时,y取最大值。(∵尽可能少裁人,∴舍去![]() )
)
答:当员工为偶数人时,裁员![]() 人,才能获得最大的经济效益;
人,才能获得最大的经济效益;
当员工为奇数人时,裁员![]() 人,才能获得最大的经济效益。………………12分
人,才能获得最大的经济效益。………………12分
21.解:(1)设所求双曲线方程为![]() ,
,
∵![]() ,∴
,∴![]() 。………………………………………………2分
。………………………………………………2分
∴渐近线斜率为![]() 。∴渐近线方程为
。∴渐近线方程为![]() 。……………………4分
。……………………4分
(2)设![]() ,
,![]() ,则
,则![]() 。
。
………………………………6分
又∵![]() ,∴
,∴![]() 。………………………………………………7分
。………………………………………………7分
∴![]() 。故
。故![]() ,……8分
,……8分
∵![]() ,∴点P的坐标为
,∴点P的坐标为![]() 。………………………………9分
。………………………………9分
设双曲线方程为![]() ,将P点坐标代入化简得
,将P点坐标代入化简得![]() ,把
,把![]() 代入得
代入得![]() ,
,![]() 。
。
∴所求双曲线方程为![]() 。……………………………………………………12分
。……………………………………………………12分
22.解:(理)(1)令x=y=0,则![]() ,∴f(0)=0。……2分
,∴f(0)=0。……2分
又令![]() ,则
,则![]() ,
,![]() ,…………4分
,…………4分
∴f(-x)= -f(x)。故f(x)在(-1,1)上为奇函数。……………………………………5分
(2)令![]() ,则
,则![]() ,
,
于是![]() 。
。
即![]() ,∴f(x)在(-1,1)上为减函数。………………………………8分
,∴f(x)在(-1,1)上为减函数。………………………………8分
从而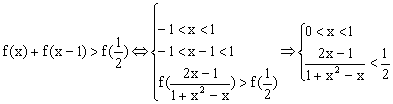 …………10分
…………10分
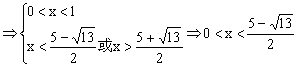 。…………………………12分
。…………………………12分
∴原不等式的解集为![]() 。……………………………………13分
。……………………………………13分
(文)(1)当a=2时,![]() ,………3分
,………3分
当且仅当![]() ,即
,即![]() 时取等号。∴f(x)的最小值为
时取等号。∴f(x)的最小值为![]() 。……5分
。……5分
(2)当0<a<1时,任取![]() ,
,![]()
……8分
∵0<a<1,且![]() ,∴
,∴![]() 。
。
∴![]() 。……………………………………………………11分
。……………………………………………………11分
从而得![]() ,∴f(x)在
,∴f(x)在![]() 上为增函数。……………………12分
上为增函数。……………………12分
∴f(x)的最小值为f(0)=a。…………………………………………………………13分