湖北省黄冈中学十一月检测题

湖北省黄冈中学十一月检测题

数 学

本试卷分第Ⅰ卷和第Ⅱ卷两部分，共150分，考试时间100分钟

第Ⅰ卷（选择题，共60分）

txjy

一、选择题（每小题5分，共60分，每小题所给的四个选项中，只有一个符合题目要求）

txjy

1.　　 两个集合A与B之差记作“A-B”，定义为A-B={xx∈A,且xB}，如果集合A={xlogx＜1,x∈R},集合B={xx-2＜1,x∈R}那么A-B等于txjy

A.{xx≤1}　　　　  B.{xx≥3}　　　 C.{x1≤x＜2}　　　　 D.{x0＜x≤1}

2.　　 已知等比数列{a}的前n项和是S=

A.8　　　　　　　　 B.12 txjy　　　　　　 C.16　　　　　　　 D.24

3.（文）e、e为基底向量，已知向量=e-ke，，若A、B、D三点共线，则k的值是

A．2　　　　　　　  B.-3 txjy　　　　　　 C.-2　　　　　　　 D.3

（理）过点（0，-1）作直线l，若直线l与圆x+（y-1）=1有公共点，则直线l的倾斜角的范围为txjy

A.［］　　　　　　　　　　　  B. ［0,∪［,π）

C.［］　　　　　　　　　　　  D. ［0,∪［）

4．命题p:不等式＞的解集为{x0＜x＜1}；命题q:在△ABC中，“A＞B”是 “sinA＞sinB”成立的必要非充分条件，则txjy

A．p真q假　　　　　 B.“p且q”为真　 C.“p或q”为假　 D.p假q真

5．编辑一个运算程序：1&1=2,m&n=k,m&(n+1)=k+3(m,n,k∈N)，则1&2004的输出结果为

A．2004　　　　　　 B.2006　　　　　  C.4008　　　　　　 D.6011

6.（文）函数y=sin(x+)（0≤≤π）是R上的偶函数，则等于

A．0　　　　  B.　　　　　　 C.　　　　　　  D.π

（理）设f（x）是函数f(x)=＜a＜1）的反函数，则使f（x）＞1成立的x的取值范围为

A．（　　　　B.(-∞,　　C.(,a)　　　D.［a,+ ∞）

7．(文)已知数列{a中，a，（n∈N），且a=1，则数列{a的通项公式a=

A.2·3　　　　　　 B.2·3-5　　　　  C.2·3+1　　　　D.2·3+1

(理)a、b、c分别是△ABC中A、B、C所对边的边长，则直线sinA·x+ay+c=0与bx-sinB·y+ay+c=0的位置关系是

A．平行　　　　　　　 B.重合　　　　　　　 C.垂直　　　　　 D.相交但不垂直

8．现行《中华人民共和国个人所得税法》规定的起征点为800元，即公民全月工资、薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计算：

全月应纳税所得税	税率
不超过500元的部分	5%
超过500元至2000元的部分	10%
超过2000元至5000元的部分	15%
……	……

为了适应时代要求，我国拟从2006年1月起将起征点由800元提高到1600元，其他均不变.小王现每月缴纳个人所得税95元，若他每月工资、薪金所得不变，则起征点提高后他每月将少缴纳_______________元

A.87.5　　　　　　　　　 B.80 txjy　　　　　　 C.75　　　　　　 D.75.5

9．要得到函数y=sin(2x-的图像，只需将函数y=cos 2x的图像

A．向右平移个单位　　　　　　　　　　　　 B.向右平移个单位

C. 向左平移个单位　　　　　　　　　　　  D. 向左平移个单位

10．（文）设点P分有向线段所成的比为则点P分所成的比为

A．-　　　　　　　  B.- 　　　　　　　C.-　　　　  D.-

(理)已知⊙C:x+y=9, ⊙C:(x-4)+(y-6)=1,两圆的外公切线交于P点，内公切线交于P点，若=λ，则λ等于

A．-　　　　　　  B.- 　　　　　　　C.-　　　　　 D.

11.（文）若tanα=2,tan(β-α)=3,则tan(β-2α)的值为

　　A．　　　　　　  B. -　　　　　　  C.　　　　　 D.-

(理)设函数f(x)的定义域为R，若存在与x无关的正常数M，使f(x)≤Mx对一切实数x均成立，则称f(x)为有界泛函，有函数f(x)=2x,g(x)=x，h(x)=2，v(x)=xsin x中，属于有界泛函的函数的个数为

A．1　　　　　　　  B.2　　　　　　　 C.3　　　　　  D.4

12.（文）定义在R上的函数f(x)满足f(x+2)=3f(x),当x∈［0,2］时，f(x)=x-2x，则当x∈［-4,-2］时，f(x)的最小值是

A．-1　　　　　　 B.- 　　　　　　　 C. 　　　　　　　D.-

 (理)已知定义域为R的函数f(x)满足f(-x)=-f(x+4)，且当x＞2时，f(x)单调递增.如果x+x＜4且(x-2)(x-2) ＜0，则f(x)+f(x)的值

A．恒小于0　　　 B.恒大于0　　　　　　 C.可能为0　　　　　 D.可正可负

第Ⅱ卷（非选择题，共90分）

二、填空题（每小题4分，共16分.把正确答案填在题中所给横线上）

13.(文)在△ABC中，若acos B=bcos A,则此三角形的形状为______________________.

（理）设x,y满足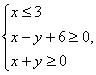则该不等式组表示的平面区域的面积为________ ;z=2x+y的最大值是________________.

14.在△ABC中，O为中线AM上的一个动点，若AM=2，则

15．已知α∈(0,且2sinα-sinαcosα-3cosα=0，则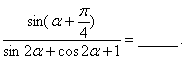

16.（文）对任意两实数a、b，定义运算“*”如下：

a　若≤b

a*b=　　　　　　 ，则函数f(x)= *logx的值域为_________.

b　若＞b

 (理)已知f(x)是定义在R上的不恒为零的函数，且对于任意的a、b∈R，满足f(a·b)=af(b)+bf(a),f(2)=2,a=（n∈N,b∈N.考查下列结论:①f(0)=f(1);②f(x)为偶函数；③数列{a为等比数列；④{b为等差数列.

其中正确的是____________.

三、解答题（共74分.解答填写出必要的文字说明、证明过程或演算步骤）

17.（本小题满分12分）

设函数f(x)=m·n，其中向量m=(2cosx,1),n=(cosx,sin2x),x∈R.

(1)　求f(x)的最小正周期；

(2)　在△ABC中，a、b、c分别是角A、B、C的对边，f(A)=2,a=,b+c=3(b＞c),求b、c的长.

18.（本小题满分12分）

已知各项均为正数的数列{a}前n项和为S，（p-1）S=p-a,n∈N，p＞0且p≠1，数列{b}满足b=2log

（1）求a，b;

（2）若p=设数列{的前n项和为T，求T.

19.（本小题满分12分）

（文）已知向量a=(1,2),b=(-2,1)，k,t为正实数，向量x=a+(t+1)b,y=-ka+

（1）若x⊥y,求k的最小值；

（2）是否存在正实数k、t,使x∥y?若存在,求出k的取值范围；若不存在，请说明理由.

（理）已知⊙M:x+(y-2)=1,Q是x轴上的动点，QA、QB分别切⊙M于A、B两点.

（1）若AB=求直线MQ的方程；

（2）求证：直线AB恒过定点，并求出此定点坐标.

20.（本小题满分12分）

现有A、B、C、D四个长方体容器，A、B的底面积均为x，高分别为x,y; C、D的底面积均为y，高也分别为x、y(其中x≠y).现规定一种两人的游戏规则：每人从四种容器中取两个盛水，盛水多者为胜，问先取者在未能确定x与y大小的情况下有没有必胜的方案？若有的话，有几种？

21．（本小题满分12分）

（文）已知函数f(x)=logp＞2，设F(x)=g(x)+f(x).

（1）求F(x)的定义域;

（2）求F(x)的值域.

(理) 已知二次函数f(x)=ax+x.

（1）若对任意x、x∈R，恒有f(≤［f(x)+f(x)］成立，求实数a的取值范围；

（2）若x∈［0,1］时，恒有f(x) ≤1，试求实数a的取值范围.

22.（本小题满分14分）

（文）已知函数f(x)=a·2+b的图像经过点A（1，，B（2，

（1）求函数y=f(x)的反函数y=f的解析式；

（2）记a=2（n∈N），是否存在正数,使得(1+)(1+)…（1+≥k∈N均成立.若存在，求出k的最大值；若不存在，请说明理由.

　

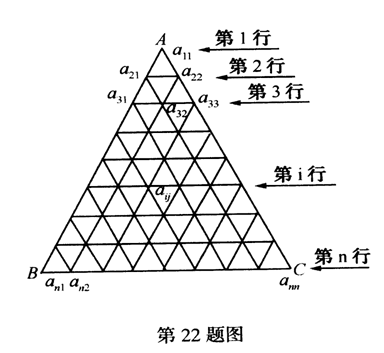
(理)如图，把正三角形ABC分成有限个全等的小正三角形，且在每个小三角形的顶点上都放置一个非零实数，使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第一行，…，BC为第n行，记点A上的数为a，…第i行中第j个数为a（1≤j≤i）.若a=

（1）求a

（2）试归纳出第n行中第m个数a表达式（用含n,m的式子表示，不必证明）；

（3）记S…+a，证明：n≤++…+≤

湖北省黄冈中学十一月检测题数学答案

1．D　2.C  3.A　4.A　5.D  6.(文)C(理)B　7.(文)A（理）C　8.C　9.B  10.（文）C（理）B 11.(文)A（理）B  12.（文）D（理）A　13.（文）等腰三角形（理）36 15　14.-2　15.

16.(文)（-∞,0]（理）①③④

17.(1)f(x)=2cosx+sin2x=1+2sin(2x+

　 ∴f(x)的最小正周期为π.

　 (2)∵f(A)=2,即1+2sin(2A＋=2,

∴sin(2A+=

∵＜2A+＜　 ∴2A+=.

由cosA==即(b+c)-a=3bc,

∴bc=2.又b+c=3(b＞c), ∴

18.（1）由(p-1)S=p-a(n∈N)　　①

　　　 得(p-1)S　　　　 ②

①-②，得≥2),

　　　 又(p-1)S=p-a,p＞0且p≠1,∴a=p.

{a}是以p为首项，，a=p(

　b=2log∴b=4-2n.

(2)由（1）知,b=4-2n,a=p.又由条件得p=得a=2.

　∴T=+　　①

　=+　　  ②

①-②得=+

=4-2×（1+

=4-2×＝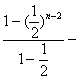

∴T=

19.（文）（1）x=a+(t

　　　　 由x⊥y,得x·y=0,即（-2t

　　　　 整理得k=

　　　　 ∵t＞0,∴k=≥2=2，当且仅当t=1时，k=2.

　　　　 所以k的最小值为2.

(2)假设存在正实数k,t使x∥y,则(-2t-1)(-2k+

　　　　  整理得tk(t+1)+1=0.

　　　　  满足上述等式的正实数k、t不存在，所以不存在正实数k、t,使x∥y.

　（理）（1）设AB交MQ于E点（如图），则易知MQ垂直平分线段AB，

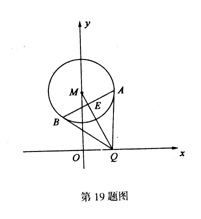　　　　∴ME==.

　　　　由射影定理知，MA

　　　　∴MQ=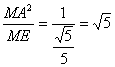

　　　  M(0,2),设Q（a,0），则MQ=

解得a=±1,即Q（1，0）或Q（-1，0）

∴直线MQ的方程为2x+y-2=0或2x-y+2=0

（2）证明：QA、QB是⊙M的切线，则MA⊥AQ,MB⊥BQ，故A、M、B、Q四点共圆且MQ是此圆直径，设此圆圆心为F.

　　设Q（a,0），则F(

　　∴⊙F的方程为即（x-

联立x项，即得两圆公共弦AB所在直线的方程：

－ax+2y-3=0

故直线AB恒过定点（0，

20.依题意可知，A、B、C、D四个容器的容积分别为x，按照游戏规则，先取者只有三种不同的取法：

　　①取A、B；②取A、C；③取A、D　问题的实质是比较两个容积和的大小.

　①若先取A、B，则后取者只能取C、D.

　 ∵(x

　 显然（x+y）＞0而x与y的大小不确定，∴(x-y)(x+y)的正负不能确定.

　 即x的大小不定，这种取法无必胜的把握.

　 ②若先取A、C，则后者只能取B、D.

　　∵(x

　　∴类似于①的分析知，这种取法也无必胜的把握.

　 ③若先取A、D，则后者只能取B、C.

∵（x

=(x+y)(x-y)，

又x≠y,x＞0,y＞0,∴(x+y)(x-y)＞0,即x＞xy+xy.

故先取A、D是惟一必胜的方案.

21．（文）（1）由题意有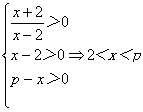

　　∴F(x)的定义域为(2,p)

　 （2）F（x）=log　x∈(2,p)

　　　令y=logt,t=(x+2)(p-x)=-x+(p-2)x+2p=-(x-

①　　 若≤2即2＜p≤6时，t时（2，p）单调递减

∴0＜t＜4(p-2)　　∴y＜log4(p-2)=2+log(p-2)

②　　 若≥p即p≤-2此种情况不可能，舍去.

③　　 若2＜＜p，即p＞6,则0＜t≤

 ∴y≤log=2log(p+2)-2

 综上知，当2＜p≤6时，F(x)的值域为(-∞，2+log(p-2));

当p＞6时，F（x）的值域为(-∞,2log(p+2)-2).

　（理）（1）对任意x、x∈R，由≥0成立.

f(x)=ax+x是二次函数，知a≠0，故要使上式成立，只有a＞0.

（2）f(x) ≤1-1≤f(x) ≤1-1≤ax+x≤1　 ……①

　　　　　  而x∈[0,1]

　　　　　 当x=0时，a≠0，①式显然成立;

　　　　　 当x∈（0，1]时，①式化为--≤a≤-

　　　　　 在x∈(0,1] 上恒成立.

　　　　  设t=，则t∈[1,+∞),则有－t－t≤a≤t-t,所以只须

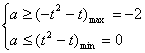
　　　　  　-2≤a≤0,又a≠0,故-2≤a＜0

　　　　  综上，所求实数a的取值范围是[-2,0)

22．（文）（1）由题知　　

　　　　  ∴f(x)=

　　　　  得出f＞

　　　　(2)a∈N

假设存在正实数k，使(1+≥kN均成立.

则k≤

记F(n)=(1+

则＞

∴F(n+1) ＞F(n), ∴F(n)随n增大而增大，F（n）的最小值为F(1)=.

∴k≤,即k的最大值为.

(理)（1）∵a∴a

∵a∴a

∵a∴a∴，a

(2)由a可归纳出a…,a

故a

由a

的等比数列，故a即a

(3)由（2）知S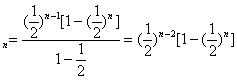

∵（N），∴（

∴（

又（

∴1≤≤2∴n≤≤