德州市高中三年级教学质量检测
数学试题(理科)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。考试时间120分钟。
第I卷(选择题 共60分)
一. 本卷共12小题,每小题5分,共计60分。在每小题列出的四个选项中,只有一项是符合题目要求的。
1. 如果全集![]() ,
,![]() ,
,![]() ,则
,则![]()
A. ![]() B.
(2,4)
B.
(2,4)
C. ![]() D.
(2,4]
D.
(2,4]
2. 命题p:![]() 是
是![]() 的一条对称轴。命题q:
的一条对称轴。命题q:![]() 是
是![]() 的最小正周期,下列复合命题:
的最小正周期,下列复合命题:
①p或q ②p且q ③非p ④非q,其中真命题有:
A. 0个 B. 1个 C. 2个 D. 3个
3. 函数![]() 的反函数是
的反函数是
A. ![]()
B. ![]()
C. ![]()
D. ![]()
4. 已知等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的值是
的值是
A. 15 B. 30 C. 31 D. 64
5. 已知函数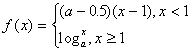 在
在![]() 内是减函数,则a的取值范围是
内是减函数,则a的取值范围是
A. (0,1) B. (0,0.5)
C. (![]() ,0.5) D.
(0.5,1)
,0.5) D.
(0.5,1)
6. 给出下列命题:
①![]() ,则
,则![]() 或
或![]()
②若![]() 为单位向量且
为单位向量且![]() ,则
,则![]()
③若![]() 且
且![]() ,则
,则![]()
④若![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,则
共线,则![]() 与
与![]() 共线
共线
其中正确命题的个数是
A. 0 B. 1 C. 2 D. 3
7. 将函数![]() 的图像按向量
的图像按向量![]() 平移后,所得图像解析式
平移后,所得图像解析式
A. ![]()
B. ![]()
C. ![]()
D. ![]()
8. 在![]() 中,A>B是
中,A>B是![]() 的( )条件
的( )条件
A. 充分不必要 B. 必要不充分
C. 充要 D. 既不充分也不必要
9. 若![]() ,则
,则![]()
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
10. 已知a>0且![]() ,函数
,函数![]() 与
与![]() 的图像只能是
的图像只能是

11. 下表给出一个“三角形数阵”
![]()
![]()
![]()
……
已知每一列的数成等差数列;从第三行起,第一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为![]() ,则
,则![]() __________。
__________。
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
12. 定义在(![]() ,0)
,0)![]() (0,
(0,![]() )上的奇函数
)上的奇函数![]() ,在(0,
,在(0,![]() )上为增函数,当x>0时,
)上为增函数,当x>0时,![]() 图像如图所示,则不等式
图像如图所示,则不等式![]() 的解集为
的解集为
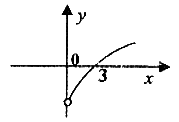
A. ![]()
B. ![]()
C. ![]()
D. ![]()
第II卷(非选择题 共90分)
二. 填空题(共4小题,每题4分,共16分)
13. 在数列![]() 中
中![]() ,则数列
,则数列![]() 的通项公式为__________。
的通项公式为__________。
14. 已知![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为钝角,则实数
的夹角为钝角,则实数![]() 的取值范围为____________。
的取值范围为____________。
15. 二次函数![]() 的部分对应值如下表,则不等式
的部分对应值如下表,则不等式![]() 的解集是_______________。
的解集是_______________。

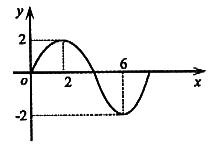
16. 若函数![]() 的部分图象如下图所示,则
的部分图象如下图所示,则![]() 。
。
三. 解答题(本大题共6个小题,满分74分。解答应写出文字说明、证明过程或演算步骤)
17. (本题满分12分)
已知![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
18. (本题满分12分)已知等比数列![]() 的公比为q,前n项和为
的公比为q,前n项和为![]() ,且
,且![]() 成等差数列。
成等差数列。
(1)求![]() 的值;
的值;
(2)求证:![]() 成等差数列。
成等差数列。
19. (本题满分12分)
设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,![]()
(1)求![]() 的最小正周期;
的最小正周期;
(2)在![]() 中,a,b,c分别是角A,B,C的对边,
中,a,b,c分别是角A,B,C的对边,![]() ,
,![]() ,
,![]() ,求b,c的长。
,求b,c的长。
20. (本题满分12分)
已知函数![]()
(1)求证:函数![]() 在(0,
在(0,![]() )上是增函数;
)上是增函数;
(2)若![]() 在[1,
在[1,![]() )上恒成立,求实数a的取值范围;
)上恒成立,求实数a的取值范围;
(3)若函数![]() 在[m,n]上的值域是
在[m,n]上的值域是![]() ,求实数a的取值范围。
,求实数a的取值范围。
21. (本题满分12分)某外商到一开发区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元。设![]() 表示前n年的纯收入(
表示前n年的纯收入(![]() 前n年的总收入-前n年的总支出-投资额)
前n年的总收入-前n年的总支出-投资额)
(1)从第几年开始获取纯利润?
(2)若干年后,外商为开始新项目,有两种处理方案:①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万元出售该厂,问哪种方案最合算?
22. (本题满分14分)
已知二次函数![]() 经过点(0,10),其导数
经过点(0,10),其导数![]() ,当
,当![]() (
(![]() )时,
)时,![]() 是整数的个数记为
是整数的个数记为![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列
,求数列![]() 的前n项(
的前n项(![]() )项和
)项和![]() 。
。
![]()
【试题答案】
德州市高中三年级教学质量检测
数学试题答案(理科)
一. 选择题(60分)
1. A 2. C 3. B 4. A 5. B 6. A
7. A 8. C 9. D 10. B 11. C 12. A
二. 填空题
13. 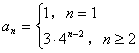
14. ![]()
15. ![]()
16. ![]()
三. 解答题
17. 解:![]()
![]() 2分
2分
![]()
![]()
![]()
又![]() 4分
4分
![]()
![]()
![]() 10分
10分
![]() 12分
12分
18. (1)解:若![]() ,则
,则![]()
故![]() 2分
2分
由![]() 成等差数列得:
成等差数列得:![]()
化简整理得:![]()
又![]() ,
,![]()
解得![]() 6分
6分
(2)证明:![]()
又![]()
![]()
![]() 即
即![]() 成等差数列 12分
成等差数列 12分
19. 解:(1)![]() 2分
2分
![]() 的最小正周期为
的最小正周期为![]() 4分
4分
(2)![]() 即
即![]()
![]() 6分
6分
![]()
![]() 8分
8分
由![]()
即![]() 10分
10分
又![]() ,
,![]() 12分
12分
20. 解:(1)![]()
![]() 在(0,
在(0,![]() )上为增函数 2分
)上为增函数 2分
(2)![]() 在(1,
在(1,![]() )上恒成立
)上恒成立
设![]()
则![]() 在(1,
在(1,![]() )上恒成立
)上恒成立
![]()
![]() 在[1,
在[1,![]() )上单调递增
)上单调递增
![]() 5分
5分
故![]() 即
即![]()
![]() 的取值范围为(
的取值范围为(![]() ,3) 7分
,3) 7分
(3)由题意知![]() 时,由(1)知
时,由(1)知![]() 在(0,
在(0,![]() )上单调递增
)上单调递增
![]() ,
,![]() 有两个不相等的正根
有两个不相等的正根
即![]() 有两个不相等的正根m,n 10分
有两个不相等的正根m,n 10分
![]()
![]() 12分
12分
21. 由题意知,每年的经费是以12为首项,4为公差的等差数列,设纯利润与年数的关系为![]() ,则
,则![]() 2分
2分
(1)纯利润就是要求![]() ,
,![]()
解得![]() 。由
。由![]() 知从第三年开始获利 4分
知从第三年开始获利 4分
(2)①年平均利润![]()
当且仅当n=6时取等号。
故此方案先获利![]() (万美元),此时n=6 7分
(万美元),此时n=6 7分
②![]()
当n=10时,![]()
故第②种方案共获利![]() (万美元) 10分
(万美元) 10分
故比较两种方案,获利都是144万美元。但第①种方案只需6年,而第②种方案需10年,故选择第①方案。 12分
22. 解:(1)设![]() ,将点(0,10)代入后,得c=10
,将点(0,10)代入后,得c=10
![]()
已知![]() ,所以
,所以![]()
所以![]() 4分
4分
![]() 在(1,2]上的值域为[4,6),所以
在(1,2]上的值域为[4,6),所以![]()
![]() 在(2,3]上的值域为(
在(2,3]上的值域为(![]() ,4],所以
,4],所以![]() 6分
6分
当![]() 时,
时,![]() 在(n,n+1]上单调递增,其值域为(
在(n,n+1]上单调递增,其值域为(![]() ]
]
所以![]()
所以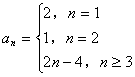 8分
8分
(2)令![]() ,则
,则![]() 10分
10分
当![]() 时,
时,![]()
![]()
![]()
12分
![]()
![]() 14分
14分