湖南省部分学校2004届第一次联考数学试题
总分150分 时量:120分钟
第Ⅰ卷 (选择题,共60分)
一、![]()
![]() 选择题:(本小题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
选择题:(本小题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
1、设全集∪={1、2、3、4、5},集合A={1、3、4},B={2、3、5},则下列集合中,表示空集的是( )
A (C![]() A)∩(C
A)∩(C![]() B) B (C
B) B (C![]() A)∩B
A)∩B
C (C![]() B)∩A D A∩B
B)∩A D A∩B
2、函数y=f(x),x∈[-2,4]的图象与直线x=2的交点个数为( )
A 0个 B 1个 C 2个 D 无数个
3、曲线![]() 在
在![]() 处的切线与圆
处的切线与圆![]() 的位置关系是( )
的位置关系是( )
A 相离 B 相切 C 相交 D 无法确定
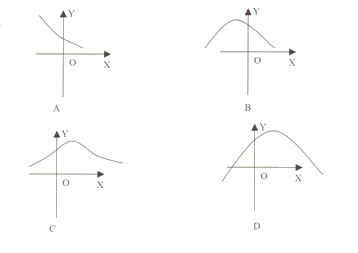
4、函数![]() (m>0)的部分图象大致是( )
(m>0)的部分图象大致是( )
5、(理)![]() (
)
(
)
A ―3+4i B ―3―4 i C 3+4 i D 3―4 i
(文)抛物线的焦点坐标是( )
A (2,0) B (1,0) C (1,1) D (0,0)
6、在等差数列![]() 中,
中,![]() ,则
,则![]() (
)
(
)
A –3 B 0 C 1 D 2
7、将4张不同的彩色图片与3张互不相同的黑白照片排成一排,任何两张黑白照片都不相邻的不同排法的种数是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
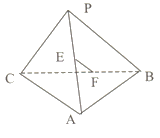 8、如图:E、F分别是三棱锥P-ABC的棱AP、BC的中点PC=10,AB=6,EF=7,则异面直线AB和PC所成的角是( )
8、如图:E、F分别是三棱锥P-ABC的棱AP、BC的中点PC=10,AB=6,EF=7,则异面直线AB和PC所成的角是( )
A
60![]() B 45
B 45![]()
C 90![]() D 120
D 120![]()
9、![]() ,
,![]() 且
且![]() ,则点M(x,y)的轨迹是( )
,则点M(x,y)的轨迹是( )
A 双曲线 B 椭圆 C 抛物线 D 双曲线一支
10、10个小球中有3个红球,随机地分配给10个小朋友,每人1个球,则最后三个分到球的小朋友恰有一个得到红球的概率为( )
A ![]() B
B 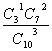
C ![]() D
D ![]()
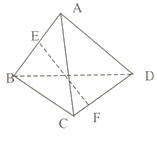
11、如图,正三棱锥A-BCD中,E在棱AB上,F棱CD上并且![]()
设α为异面直线EF与AC所成的角,β为异面直线EF与BD所成的角,则α+β的值是( ).
![]() A
A ![]() B
B ![]()
C ![]() D 与λ有关的变量
D 与λ有关的变量
12、(理)参数方程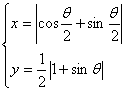 (θ为参数,且0<θ<π),表示( )
(θ为参数,且0<θ<π),表示( )
A 过点A(1,![]() )的双曲线 B
过点A(1,
)的双曲线 B
过点A(1,![]() )的抛物线的一部分
)的抛物线的一部分
C 过点A(1,![]() )的椭圆的一部分 D 过点A(1,
)的椭圆的一部分 D 过点A(1,![]() )的圆弧.
)的圆弧.
(文)以过抛物线的焦点F的弦为直径的圆与抛物线的准线的位置关系是( )
A 相离 B 相交 C 相切 与P有关
第Ⅱ卷(共90分)
二、填空题,(本题共4个小题,每小题4分,共16分)
13、(理)定义符号函数 则不等式:
则不等式:![]() 的解集是_______________.
的解集是_______________.
(文)不等式![]() 的解集是___________________.
的解集是___________________.
14、设![]() 是定义在R上的奇函数,且
是定义在R上的奇函数,且![]()
15、二项式![]() 展开式中各项的二项式系数和为1024,且二项式系数最大的项系数为252,则
展开式中各项的二项式系数和为1024,且二项式系数最大的项系数为252,则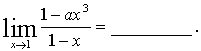
16、若对n个向量![]() 存在n个不全为零的实数
存在n个不全为零的实数![]() ,使得
,使得![]() 成立,则称向量
成立,则称向量![]() 为“线性相关”,依此规定能说明
为“线性相关”,依此规定能说明![]() “线性相关”的实数
“线性相关”的实数![]() 依次可以取__________(写出一组即可).
依次可以取__________(写出一组即可).
三 解答题:
17、(12分)已知![]() ,设
,设![]()
(1) 求![]() 的最小正周期;
的最小正周期;
(2) 求![]() 的单调递增区间.
的单调递增区间.
18、(文)设人的某一特征是由他的一对基因决定的,以d表示显性基因,r表示隐性基因。则具有dd基因的人为纯显性,具有rr基因的人是纯隐性,具有rd基因的人为混合性。纯显性与混合性的人都显露显性基因的某一特征。孩子从父母身上各得到1个基因。假定父母都是混合性的,问:
(1) 1个孩子有显性基因决定的特征的概率为多少?
(2) 2个孩子中至少有一个有显性基因决定的特征的概率为多少?
(理)(12分)某超市为扩大销售调查进入该超市顾客的人数,经观察,在一段时间内,进入超市为n个人的概率为p (n)满足关系
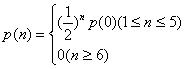
(1) 求一个顾客也没有的概率p(0)
(2) 求一段时间进入该超市顾客的期望值。
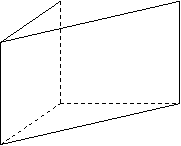
19、(12分)如图:直三棱柱 ![]() -
-![]() 中,已知∠ABC=90
中,已知∠ABC=90![]() ,AB=BC=BB
,AB=BC=BB![]() =1.
=1.
(1) 求异面直线AB![]() 与BC
与BC![]() 所成的角;
所成的角;
(2) 
![]() 求二面角A-
求二面角A-![]() -A
-A![]() 的大小.
B
的大小.
B![]() C
C![]()
A![]()
B C
A
20、(12分)已知椭圆![]() 的离心率
的离心率![]() ,过点A(0,-b),和B(a,0)的直线与原点的距离为
,过点A(0,-b),和B(a,0)的直线与原点的距离为![]() .
.
(1) 求椭圆的方程;
(2) 已知定点E(-1,0),若直线![]() 与椭圆交于C、D两点问:是否存在k的值,使得CD为直径的圆过E点?请说明理由。
与椭圆交于C、D两点问:是否存在k的值,使得CD为直径的圆过E点?请说明理由。
21、(12分)(文)在数列![]() 中,
中,![]() ),
),![]()
(1) 求![]() 的通项公式;
的通项公式;
(2) 设![]() 对一切n∈N
对一切n∈N![]() 恒成立的最小正整数m的值。
恒成立的最小正整数m的值。
(理)(12分)设函数![]() ,定义域为R,当
,定义域为R,当![]() 时,
时,![]() ,且对于任意的
,且对于任意的![]() ,有
,有![]() 成立,数列
成立,数列![]() 满足
满足![]()
(1) 求![]() ;
;
(2) 判断![]() 的单调性;
的单调性;
(3) 求![]() 的通项公式。
的通项公式。
22、(14分)设函数![]() 在定义域D内,存在
在定义域D内,存在![]() ,使
,使![]() 成立,则称点
成立,则称点![]() 为函数
为函数![]() 图象上的不动点。
图象上的不动点。
(1) 若函数![]() 的图象上有且仅有一个不动点,求
的图象上有且仅有一个不动点,求![]() 的解析式;
的解析式;
(2) 对(1)中的b值,设![]() 图象上有两个不动点A,B,P为
图象上有两个不动点A,B,P为![]() 图象上的另一个不同与A、B的点,且
图象上的另一个不同与A、B的点,且![]() ,求点P到直线AB距离的最小值及取得最小值时的P的坐标。
,求点P到直线AB距离的最小值及取得最小值时的P的坐标。