培优练习(2)2004-03-02
一、选择题:
1、由方程 ![]() 确定的函数y = f (x)在(-∞,+ ∞)上是
确定的函数y = f (x)在(-∞,+ ∞)上是
A.奇函数 B.偶函数 C.增函数 D.减函数
2、设奇函数![]() 上是增函数,且
上是增函数,且![]() 若函数
若函数![]() 对所有
对所有
的![]() 都成立,当
都成立,当![]() 时,则t的取值范围是
时,则t的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3、从-3,-2,-1,1,2,3中任取三个不同的数作为椭圆方程![]() 中的系
中的系
数,则确定不同椭圆的个数为
A .17 B.
18 C.
19 D.
20
4、过双曲线![]() 的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P
的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P
点,则有![]() 的定值为
的定值为![]() 类比双曲线这一结论,在椭圆
类比双曲线这一结论,在椭圆![]() (a>b
(a>b
>0)中,![]() 是定值
是定值
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
二、填空题
5、设等比数列![]() 的前n项和为
的前n项和为![]() ,前n+1项的和为
,前n+1项的和为![]() ,
,![]() =______.
=______.
6、在一个棱长为![]() 的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm
.
的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm
.
7、已知函数![]() 的值域为R,且f(x)在(
的值域为R,且f(x)在(![]() 上是增函数,则a的范围是 .
上是增函数,则a的范围是 .
8、已知函数f(x) = 2x![]() -x,则使得数列{
-x,则使得数列{![]() }(n∈N
}(n∈N![]() )成等差数列的非零常数p与q所满足的关系式为
.
)成等差数列的非零常数p与q所满足的关系式为
.
三、解答题
9、(本题满分12分)
某工厂最近用50万元购买一台德国仿型铣床,在买回来以后的第二天投入使用,使用后的第t天应付的保养费是(t + 500)元,(买来当天的保养维修费以t = 0计算),机器从买来当天到报废共付的保养维修费与购买机器费用的和平均摊到每一天的费用叫做每天的平均损耗.当平均损耗达到最小值时,机器报废最划算.(1) 求每天平均损耗y (元)表示为天数x的函数;(2) 求该机器买回来后多少天应报废.
10、(本题满分12分)
已知 f (θ) = a sin θ + b cos θ,θ Î [ 0, p ],且1与2 cos 2 的等差中项大于1与 sin 2 的等比中项的平方.求:(1) 当a = 4, b = 3时,f (θ) 的最大值及相应的 θ 值;(2) 当a > b > 0时,f (θ) 的值域.
11、(本题满分12分)
已知椭圆C的方程为x 2 + = 1,点P(a, b)的坐标满足a 2 + ≤ 1,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:(1) 点Q的轨迹方程;(2) 点Q的轨迹与坐标轴交点个数。
12、(本题满分12分)
(1) 直线m:y = kx + 1与双曲线x 2-y 2 = 1的左支交于A、B两点。求k的取值范围;(2) 直线l过点P(-2, 0)及线段AB的中点,CD是y轴上一条线段,对任意的直线l都与线段CD无公共点。试问CD长的最大值是否存在?若存在,请求出;若不存在,则说明理由。
13、(本题满分12分)
已知函数![]() .
.
(1)求![]() 及
及![]() 的值;
的值;
(2)是否存在自然数![]() ,使
,使![]() 对一切
对一切![]() 都成立,若存在,求出自然数
都成立,若存在,求出自然数![]() 的最小值;不存在,说明理由;
的最小值;不存在,说明理由;
(3)利用(2)的结论来比较![]() 和
和![]()
![]() 的大小.
的大小.
14、(本题满分12分)
已知二次函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值为M .
的最大值为M .
(Ⅰ)试证明![]() ;
;
(Ⅱ)试证明![]() ;
;
(Ⅲ)当![]() 时,试求出
时,试求出![]() 的解析式.
的解析式.
参考答案
一、选择题:DCBA
二、填空题:5、 6、4 7、0≤a≤2 8、p=-2q
三、解答题:
9、解:(1)第一天应付维修保养费a1 = 500元;
第二天应付维修保养费a2 = (500 + 1) 元;
第三天应付维修保养费a3 =(500 + 2)元;
┄
第x天应付维修保养费ax = [500 + (x-1)] 元. 2分
由此可知 {a n} 是首项a1 = 500,公差d = 1的等差数列,
∴ 前x天共付维修保养费Sx = a1x + d = 500x + , 4分
因而,每天平均费用y与时间x (天数)的函数关系为
y = (x Î N*) ,
即y = + + (x Î N*) . 7分
(2) 即y = + + ≥2 + = 1000 + = ,
当且仅当= ,即x = 1000时取等号, 11分
∴ x = 1000天时,机器报废最合算。 12分
10、解:易得>sin2,
∴ 1 + 2cos2>2 sin2,即2(cos2-sin2) > -1,
∴ 2cosq > -1,即cosq >-.
∵ q Î [0,p ],∴ q Î [0, ) . 2分
(1)当a = 4,b = 3时,有f(q ) = 4sinq + 3cosq = 5sin(q + j ) (其中j = arctan ).
∵ 0≤q <,∴ j ≤q + j < + j ,而0<j = arctan <.
∴ 当q + j = 即q = -arctan 时,f(q )max = 5. 5分
(2)由(1)知,当a>b>0时,设 , 则有 + = 1。
∵ 0≤q <, ∴ 0≤y≤a , -<x≤b,其方程表示一段椭圆弧,端点为M(b,0),
N(-,),但不含N点。 7分
设f(q ) = x + y = t,则y = -x + t为一直线。
将y = -x + t代入+ = 1可得(a2 + b2)x2-2b2tx + b2(t2-a2) = 0。
当直线与椭圆相切时,有△ = 4b4t2-4b2(a2 + b2)(t2-a2) = 4b2[b2t2-(a2 + b2) (t2-a2)] = 0。
求得t = ±,∴ f(q )max = 。 9分
当直线过点M(b,0)时,有f(q ) = b;当直线过点M(-,)时,有f(q ) = 。
当a<b时,f(q )min = ;当a≥b时,f(q )min =b。 11分
故当0<b<a<b时,f(q ) Î (,];当a≥b>0时,f(q ) Î [b,]。12分
11、解:设A(x1,y1)、B(x2,y2)、Q(x,y),
(1) ①当x1 ≠ x2时,不妨设直线l的斜率为k,其方程为y = k(x-a) + b,
由 可得(x1-x2)(x1 +x2) + (y1 -y2 )(y1 + y2) = 0,
∴ + · · = 0, 3分
由x = ,y = , 且 = ,
∴Q点的轨迹方程为2x2 + y2-2ax-by = 0 . (*) 6分
②当x1 = x2时,斜率k不存在,此时,l//y轴,
∴ AB的中点Q必在x轴上,即Q(a,0),显然满足方程(*)。 7分
综上,Q点的轨迹方程为2x2 + y2-2ax-by = 0. 8分
(2) 当a = b = 0时,Q点的轨迹与坐标轴只有一个交点(0,0);
当a = 0,0< b ≤时,Q点的轨迹与坐标轴有两个交点(0,0),(0,b);
当b = 0,0< a ≤1时,Q点的轨迹与坐标轴有两个交点(0,0),(a,0);
当0< a <1,0< b <时,Q点的轨迹与坐标轴有三个交点(0,0),(a,0),(0,b).
12分
12、(1)解 得(1-k2)x2-2kx-2 = 0。 1分
直线与双曲线左分支有两个交点,不妨设A(x1,y1),B(x2,y2),
则有,解得1<k<. 5分
(2)设AB中点为M(x,y),则 ,
直线l:y = (x + 2), 7分
代入x = 0,交y轴于(0,b),则b = 。 8分
又f(k) = -2k2 + k+ 2 = -2(k-)2 + 在k Î (1,)上是减函数,
∴ -2 = f()<f(k)<f(1) = 1,
∴ b<-(2 + )或b>2, 10分
故与l无公共点的线段CD长有最大值2-[-(2 + )] = 4 + 。 12分
13、解(1)![]() ;
;![]() .2分
.2分
(2)假设存在自然数![]() ,使
,使![]() 对一切
对一切![]() 都成立.
都成立.
由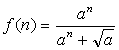 ,
,![]() 得
得 ![]() , 4分
, 4分
当![]() 时,不等式
时,不等式![]() 显然不成立.
5分
显然不成立.
5分
当![]() 时,
时,![]() ,
,
当![]() 时,显然
时,显然![]() ,
6分
,
6分
当![]() 时,
时,![]() =
=![]() 成立,则
成立,则 ![]() 对一切
对一切![]() 都成立.
8分
都成立.
8分
所以存在最小自然数![]() 。
9分
。
9分
(3). 由![]()
![]() (
(![]() ),所以
),所以![]() ,
,![]() ,……,
,……,![]() ,
,
相乘得![]() , 11分
, 11分
∴ ![]()
![]() 成立.
12分
成立.
12分
14、(Ⅰ)证明:∵![]() ,
, ![]()
![]()
![]()
∴![]() 3分
3分
(Ⅱ)证明:依题意,![]() ,
,![]() ,
, ![]()
又![]() ,
,![]() ,
,![]() 5分
5分
∴ ![]()
![]()
![]() ,
,
∴![]() 7分
7分
(Ⅲ)依![]() 时,
时,![]() ,
,![]() ①
①
同理![]() ②
②
![]() ③
9分
③
9分
②+③得:![]() ④
由①、④得:
④
由①、④得:![]() .
.
当![]() 时,分别代入②、③得:
时,分别代入②、③得:![]() ,
11分
,
11分
因此![]() .
12分
.
12分