§1.1 集合的概念与运算
【复习目标】1、理解集合、子集、交集、并集、补集的概念，了解空集和全集的意义，了解属于、包含、相等关系的意义，能够掌握有关的术语和符号，能正确地表示一些较简单的集合。2、理解并掌握集合交、并、补的运算法则，能够运用集合语言与集合思想解决有关问题。
【基础训练】1、若集合
，则
等于_____
A 
B 
C 
D 
2、集合
的子集个数是_____
A 32 B 31 C 16 D 15
3、不等式组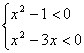
的解集是_____
A 
B 
C 
D 
4、设
是全集，非空集合P、Q满足
，若求含P、Q的一个集合运算表达式，使运算结果为空集
，则这个运算表达式可以是_____
5、已知集合A={0,1},B={
,C={
}，则A、B、C之间的关系是_____
6、已知全集U={
取不大于30的质数},A、B是U的两个子集,且
，
则A=______，B=_____
【例题】1、设集合A={
且
}，B={且
}，则
中的元素的个数是___
A 11 B 10 C 16 D 15
2、已知A=
，B=
且
，
求
的值。
3、已知
，若
，求
的值。
4、已知集合
，如果
，求实数
的取值范围。
§1.2 逻辑联结词与四种命题
【复习目标】了解命题的概念和命题的构成；理解逻辑联结词“或”“且”“非”的含义；理解四种命题及其相互关系。
【基础训练】1、由“p：8+7=16,q：
”构成的复合命题，下列判断正确的是_____
A p或q为真，p且q为假，非p为真 B p或q为假，p且q为假，非p为真
C p或q为真，p且q为假，非p为假 D p或q为假，p且q为真，非p为真
2、对于命题“正方形的四个内角相等”，下面判断正确的是_____
A 所给命题为假 B 它的逆否命题为真 C 它的逆命题为真 D 它的否命题为真
3、下列命题中，是简单命题的只有_____
(1) 12是4和3的公倍数 (2)相似三角形的对应边不一定相等 (3)三角形中位线平行且等于底边长的一半 (4)等腰三角形的底角相等
A (1)(2)(4) B (1)(4) C (2)(4) D (4)
4、命题p：0不是自然数，命题q：
是无理数，则在命题“p或q”“p且q”“非p”
“非q”中真命题是____，假命题是______。
5、命题“若
，则
”与它的逆命题、否命题、逆否命题中，真命题的个数为_____
【例题】1、给出命题：“已知
是实数，若
，则
”，对其原命题、逆命题、否命题、逆否命题而言，真命题是_____
A 0个 B 2个 C 个 D 4个
2、写出命题“当
时，
或
或
”的逆命题、否命题、逆否命题，并判断它们的真假。
3、指出下列复合命题的构成形式：(1)实数的平方不是负数；(2)4是12和16的一个公约数；(3)一个内角是直角的菱形是正方形，对角线垂直的矩形也是正方形。
4、判断并证明下列命题的真假：(1)如果一个整数
的平方是偶数，那么这个整数本身也是偶数；(2)不存在实数
，使抛物线
与
轴只有一个交点。
5、在一次模拟打飞机的游戏中，小李接连射击了两次，设命题p1是“第一次射击击中飞机”，命题p2是“第二次射击击中飞机”，试用p1, p2及联结词“或”“且”“非”表示下列命题：(1)两次都击中飞机；(2)两次都没有击中飞机；(3)恰有一次击中飞机;(3)至少有一次击中飞机；
§1.3 充要条件与反证法
【复习目标】掌握充分必要条件的意义，能够判定给定的两个命题的充要关系。
【基础训练】1、“
”是“
”的______
A 充要条件 B 充分条件 C 必要不充分条件 D 非充分也非必要条件
2、已知p：
q：
，则
是
的____
A 充分而不必要条件 B 必要而不充分条件 C 充要条件 D 既不充分也不必要条件
3、已知p：－5<x<1,条件q：x2=4，则p是q的______
A 充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要条件
4、集合
，则“
”是“
或
”的____条件。
5、方程
至少有一个负的实数根的充要条件是_______
【例题】1、已知实系数一元二次方程
在下列结论中正确的是______
(1)
是方程有实根的充分条件 (2) 是这个方程有实根的必要条件 (3) 是这个方程有实根的充要条件 (4) 
是这个方程有实根的充分条件
A (3) B (1)(2) C (1)(2)(3) D (1)(2)(3)(4)
2、下列说法对不对？如果不对，分析错误的原因：
(1)
是
的充分条件；(2)是的必要条件；
3、已知
，求证：
的充要条件是
(二次不等式的开方解法)
4、求证一元二次方程
最多有两个不相等的根。
5、已知数列
的前和
(
且
)，求数列成等比数列的充要条件。
第一章单元测试
1、如果A=
，那么错误的结论是______
A 0∈A B {0}
A C 
D A
2、下列四个命题，其中正确的有_____
(1)与1非常接近的全体实数能构成集合；(2)
表示一个集合；(3)空集是任何一个集合的真子集；(4)任何两个非空集合必有两个以上的子集
A 0个 B 1个 C 2个 D 3个
3、集合
,且
,则的值为____
A －1 B 1 C －2 D 2
4、如果
，那么______
A ST B TS C S=T D
S
T
5、下列判断正确的个数为______(1)
或
是正确的；(2)命题5<2且7>3为真；(3)
说法是不正确的；(4)原命题为假，则它的否命题不一定为假
A 0 B 1 C 2 D 3
6、若
是两个简单命题，且“p或q”的否定是真命题，则必有______
A p真q真 B p假q假 C p真q假 D p假q真
7、若
有负值，则的取值范围是______
A 
或
B 
C 
D 
8、设
均为非零实数，不等式
和
的解集分别为集合M和N，那么“
”是“M=N”的____
A 充分非必要条件 B 必要非充分条件 C 充要条件 D 既不充分也不必要条件
9、已知
有且仅有整数解；q：a,b是整数；则p是q的_____
A 充分不必要条件 B 充要条件 C 必要不充分条件 D 既不充分也不必要条件
10、用反证法证明如果a>b，那么
，假设的内容应是______
A 
B 
C
且 D 或
11、设集合
，若
，则
与集合M、N的关系是______
A ∈M B 
C ∈N D 
N
12、下列四个命题中，与命题A
B等价的共有_____
(1)
；(2)
；(3)
；(4)
A 1个 B 2个 C 3个 D 4个
13、设集合
,则集合{
且
}=___
14、在100个学生中，有篮球爱好者60人，排球爱好者65人，则既爱好篮球又爱好排球的人数最少有____个，最多有_____个。
15、已知集合
，若
是平面上正八边形的顶点所构成的集合，则的值是_____
16、所给命题：(1)“菱形的对角线互相平分”的逆命题；(2)
或
；(3)对于命题p且q，若p假q真，则p且q为假；(4)“有两条边相等且有一个角是60°”是
“一个三角形为等边三角形”的充要条件。其中为真的序号为______
1、函数
在区间
上的最大值为______，最小值为_______
2、求函数
的单调区间。
3、设函数
当
时有极值。求：(1)
的表达式；(2) 的极值；
4、已知函数=
。求的极大值与极小值。
5、已知函数
为偶函数，它的图象过点A(0，－1)且在
处的切线方程为
。求(1)函数的解析式；(2)函数
的最大值及相应的的值。