数学理科 模拟试卷一
一、选择题
1. 设集合
,
则M∩N是( )
（Ａ） {2,5} （Ｂ） {3,2}
（Ｃ） {(3,2)} （Ｄ） {(5,2)}
2. 已知函数
,
，其中即不是奇函数又不是偶函数的是( )
（Ａ） f1(x)与f2(x) （Ｂ） f1(x)与f3(x)
（Ｃ） f2(x)与f3(x) （Ｄ） f3(x)与f4(x)
3. (1+x)
展开式中x
的系数与x
的系数之和等于(1+x)
展开式中( )
（Ａ） x 的系数
（Ｂ） x
的系数
（Ｃ） x
的系数
（Ｄ） x
的系数
4. 函数y=2sin
x-6sinx+4 的值域是(
)
（Ａ） [0,12] （Ｂ） [0,11]
（Ｃ） [-1,1] （Ｄ） [5,10]
5. 已知直线 x=3+4t
（t是参数 ），则下列命题中错误的是( )
y=-4+3t
（Ａ） 直线过点(1,-11/2)
（Ｂ）
直线的倾斜角是arctg（
）
（Ｃ） 直线不经过第二象限
（Ｄ）
当t=1时，直线对应的点到点（1，2）的距离是
6. 函数y=arccos
的值域是( )
（Ａ） [0,π] （Ｂ） [π,2π]
（Ｃ） (0,
]
（Ｄ） [0, )
7. 已知命题甲是“x∈{x
≥0}”，命题乙是“{xlog3(2*x+1)≤0}”，则( )
（Ａ）甲是乙的充分条件，但不是乙的必要条件
（Ｂ）甲是乙的必要条件，但不是乙的充分条件
（Ｃ）甲是乙的充分必要条件
（Ｄ）甲即不是乙的充分条件，也不是乙的必要条件
8. 有两个同心圆，在外圆周上有不重合的六个点，在内圆周上有不重合的三个点，由这九
个点决定的直线最少有( )
（Ａ）18条 （Ｂ）21条
（Ｃ）33条 （Ｄ）36条
9. 设平面α⊥平面β，又直线mα,nβ，且m⊥n，则( )
（Ａ） m⊥β （Ｂ） n⊥α
（Ｃ） m⊥β且n⊥α （Ｄ） m⊥β或n⊥α
10. 一个等边圆柱（圆柱的底面直径与高相等）的侧面积是球的表面积4倍，则圆柱的体
积是球的体积的( )
（Ａ） 12倍 （Ｂ） 10倍
（Ｃ） 8倍 （Ｄ） 4倍
11. 设点(sinθ,cosθ)到直线xcosθ+ysinθ+1=0的距离小于
，则θ的取值范围是
( )
（Ａ） 
,
k∈Z
（Ｂ） 
, k∈Z
（Ｃ） 
, k∈Z
（Ｄ） 
）, k∈Z
12. 复数z满足
则z+3-3i+z-3i的最小值是( )
（Ａ） 
（Ｂ）
（Ｃ） 
（Ｄ）
13. 抛物线y=x-2xsinα+1的顶点在椭圆x+4y=1上，
这样的抛物线共有( )
（Ａ） 一条 （Ｂ） 两条
（Ｃ） 三条 （Ｄ） 四条
14. 已知
在第四象限且
，则sinθ等于( )
（Ａ） 
（Ｂ）
（Ｃ） 
（Ｄ）
15. 已知 OA、OB是圆锥底面互相垂直的两条半径，C是母线SB的中点，SA＝3，OA＝2，
则A、C两点在圆锥侧面上的最短距离是( )
（Ａ） 
（Ｂ）
（Ｃ）
（Ｄ）
二、填空题
16. 把双曲线方程
化为直角坐标方程是( )
（Ａ）3x-y+12x+9=0
（Ｂ） 3x+y+12x+9=0
（Ｃ）3x-y-12x+9=0 （Ｄ） 3x+y+12x-9=0
17. 如果z和z-z+1-i都是纯虚数，那么z等于( )
（Ａ） -i （Ｂ） i
（Ｃ） +-i （Ｄ） 2i
18. 在数列{a
}中，a1=sinθ≠0, an+1=acosθ (n∈N),
如果 
，则θ的值等于( )
（Ａ）
(k∈Z) （Ｂ）
(k∈Z)
（Ｃ）
(k∈Z) （Ｄ） 
(k∈Z)
19. 过椭圆
的左焦点作一条长为
的弦AB，将椭圆绕着其左准线在空间旋
转120度，则弦AB扫过的面积为( )
（Ａ） π （Ｂ） 2π
（Ｃ） 6π
（Ｄ） 
三、解答题
20. 已知函数f(x)=
sin
x+cosx-1，求函数f(x)的最小正周期与单调减区间。
函数的最小正周期为( )
（Ａ） π
（Ｂ） （Ｃ）
（Ｄ） 2π
函数的单调区间为( )
（Ａ） [Kπ，+kπ] (k∈Z) （Ｂ） [2Kπ，（）+2kπ] k∈Z
（Ｃ） [
，（
）+
] k∈Z （Ｄ） [，（）+] k∈Z
[分析解答]
|
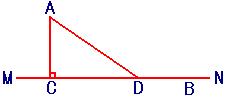
21. 如图，假设河的一条岸边为直线MN，又AC⊥MN于C，点B、D在MN上。先需将货物从A处运往B处，经陆路AD与水路DB.已知AC=10公里，BC=30公里，又陆路单位距离的运费是水路运费的两倍，为使运费最少，D点应选在距离C点多远处? ( ) （Ａ） |
公里 （Ｂ） 
公里 （Ｃ） 
公里 （Ｄ） 
公里
[分析解答]
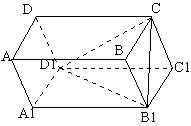
22. 如图：在平行六面体ABCD-A1B1C1D1中，
|
已知AB=AD=2a, AA1=a,∠A1AD=∠A1AB=∠DAB=60度 （Ⅰ） 求证：AA1⊥平面B1CD1； （Ⅱ） 求平行六面体ABCD-A1B1C1D1的体积。 |
[分析解答]
23. 设等差数列{a}的前n项和为S，已知S4=44,S7=35
（Ⅰ）求数列{a}的通项公式与前n项和公式；
（Ⅱ）求数列的前n项和Tn。
[分析解答]
|
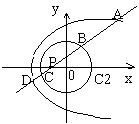
24. 已知抛物线C1: y = x+7与圆C2:x+y=5. （Ⅰ）求证：抛物线C1与圆C2无交点； （Ⅱ）过点P(a,0)作与X轴不垂直的直线l交C1于A、D两点， 交C2于B、C两点（如图），且AB=CD， 求a的取值范围。 |
[分析解答]
25.（Ⅰ）设t>0,
试求f(t)的最小值与g(t)的最大值；
（Ⅱ）设
, 
, c=x+y,
试讨论：是否存在正数p，使得对任意的正数x和y，以a、b、c
为三边长的三角形存在。若存在，求出存在时p的取值范围；
若不存在，说明理由。
[分析解答]
参 考 答 案
一、
1. D 2. C 3. B 4. A 5. D
6. D 7. B 8. B 9. D 10. D
11. B 12. B 13. D 14. A 15. C
二、
16. A 17. B 18. D 19. C
三、
20. B； C
[分析解答]
(i) f(x)=(
)cos4x-
∴ f(x)的最小正周期为
(ii) 由2kπ≤4x≤2kπ+π(k∈Z)知f(x)单调区间为[，+] k∈Z
21. B
[分析解答]设CD＝x公里，设水路运价每公里为a元，则陆路运价为每公里2a元，
运费 
(0≤x≤30)
令
, 则
, 平方得3x-2zx+(400-z)=0
由x∈R, 得△=4z-4×3(400-z)≥0
由z≥0 解得z≥
,当且仅当
时 
因此当时y有最小值，故当
公里时，运费最少。
注：对于
，也可以设x=10tgθ(0≤θ＜)去解。
22.
[分析解答]
.
23.
[分析解答]
（Ⅰ）设数列的公差为d，由已知S4=44,S7=35可得a1=17,d=-4
∴a=-4n+21 (n∈N),S=-2n+19 (n∈N).
（Ⅱ）由a=-4n+21≥0 得n≤
, 故当n≤5时，a≥0, 当n≥6时，a〈0.
当n≤5时,T=S=-2n+19n 当n≥6时,T=2S5-S=2n-19n+90.
24. [分析解答]
(Ⅰ)略 (Ⅱ)-10<a<-（）.
25.
[分析解答]
（Ⅰ）∵t>0,∴f(t)≥2+
(当且仅当t=1时取等号)，故f(t)的最小值为2+
∵t>0, ∴ 
≤
(当且仅当t=1时取等号)
故g(t)的最大值为
（Ⅱ）由（Ⅰ）可知：当〈p〈
时，以a,b,c为边长的三角形总存在。