综合练习(一)
2002.4
班级:_________, 姓名:___________,成绩:___________
一、选择题:(每小题5分,共5×12=60分)将正确答案填入下表中
1.已知集合![]() ,
,
![]() .若P∩Q≠φ,则a,b应满足
.若P∩Q≠φ,则a,b应满足
(A)a≤1且b≤1
(B)![]() 且
且![]()
(C)![]()
(D)![]()
2.若![]() ,
,![]() ,则θ的终边在
,则θ的终边在
(A)第一象限(B)第二象限
(C)第一象限或第三象限(D)第四象限
3.设α、β表示平面,l表示直线,且![]() ,
,![]() .存在下列三个事实:①l⊥α②l∥β③α⊥β .若以其中两个作为条件,另一个作为结论,则可以构成三个命题。在这三个命题中,正确命题的个数是
.存在下列三个事实:①l⊥α②l∥β③α⊥β .若以其中两个作为条件,另一个作为结论,则可以构成三个命题。在这三个命题中,正确命题的个数是
(A)0(B)1(C)2(D)3
4.把函数![]() 的图象向左平移m(m>0)个单位,所得图象关于y轴对称,则m的最小正值是
的图象向左平移m(m>0)个单位,所得图象关于y轴对称,则m的最小正值是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.已知方程![]() 的两个虚根为
的两个虚根为![]() ,
,![]() ,且
,且![]() ,则实数m的值是
,则实数m的值是
(A)5(B)![]()
(C)![]() (D)
(D)![]()
6.(理)圆![]() 的圆心的极坐标为
的圆心的极坐标为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(文)曲线![]() 与直线y=k(x-2)+4有两个交点时,实数k的取值范围是
与直线y=k(x-2)+4有两个交点时,实数k的取值范围是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
7.将圆心角为120°,半径为30的扇形OAB(O为圆心)卷成一个圆锥,使两条半径OA、OB重合,则扇形中的弦AB上的点到圆锥底面的最远距离是
(A)![]() (B)10
(B)10
(C)15(D)![]()
8.从12个化学实验小组(每小组4人)中选出5人,进行5个不同的化学实验,且每小组至多选1人,则不同的安排方法的种数是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
9.设![]() ,
,![]() ,则M,N的大小关系为
,则M,N的大小关系为
(A)M>N(B)M=N
(C)M<N(D)不能确定
10.双曲线![]() 的一条准线被它的两条渐近线截得的线段的长度等于它的一个焦点到一条渐近线的距离则双曲线的两条渐近线的夹角为
的一条准线被它的两条渐近线截得的线段的长度等于它的一个焦点到一条渐近线的距离则双曲线的两条渐近线的夹角为
(A)120°(B)90°(C)60°(D)30°
11.已知函数y=f(x)的反函数与函数y=g(x)的图象关于点P(a,b)对称,则g(x)可表示为
(A)![]()
(B)![]()
(C)![]()
(D)![]()
12.已知⊙O的半径为r,O点到直线l的距离OA=m,P是圆周上一点,且∠POA=θ。一质点从P点出发,以T秒一周的速度绕O点在圆周上逆时针作匀速圆周运动。若t秒后在Q点,则Q点到直线l的距离QR等于
(A)m-rcosθ
(B)![]()
(C)![]()
(D)![]()
二.填空题:(第小题4分,共4×4=16分)
13.若A为△ABC的内角,则sinA+cosA的取值范围是______________________。
14.不等式![]() 的解的区间表示是______________________
的解的区间表示是______________________
15.已知![]() 分别是二项式
分别是二项式![]() 和
和![]() 展开式的各项系数和,则
展开式的各项系数和,则![]() 。
。
16.降水量是指水平地面上单位面积的降雨水的深度,用上口直径为38cm,底面直径为24cm且高为35cm的倒圆台形水桶来测量降水量,如果在一次降雨过程中,用此桶接得的雨水正好是桶深的![]() ,则本次下雨的降水量是_____mm(精确到1mm)。
,则本次下雨的降水量是_____mm(精确到1mm)。
三.解答题:(第17~21题每题12分,第22题14分,共74分)
17.在复平面上复数![]() 对应的点为
对应的点为![]() ,将向量
,将向量![]() 依顺时针方向旋转锐角α得到向量
依顺时针方向旋转锐角α得到向量![]() ,且
,且![]() 。若△ABC中,
。若△ABC中,![]() ,
,![]() ,最长的边长为1。(1)求角C的大小;(2)求最短边的边长。
,最长的边长为1。(1)求角C的大小;(2)求最短边的边长。
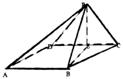
18.已知四棱锥P-ABCD的底面是边长为a的菱形,且∠BAD=60°,侧面PDC⊥底面ABCD,又△PDC为等边三角形,E为DC中点。(1)求证:AB⊥平面PBE;(2)求PA与平面PBE所成的角;(3)求二面角P-AD-B的大小。
19.设a>0,解关于x的方程![]() 。
。
20.某公司取消福利分房和公费医疗,实行年薪制工资结构改革,并按下表规定实施:
| 项目 | 金额(元/人,年) | 性质与计算方法 |
| 基础工资 | 10000 | 考虑物价因素从2002年起每年递增10%(与工龄无关) |
| 房屋补贴 | 400 | 按职工在公司任职年限,每年递增400元 |
| 医疗费 | 1600 | 固定不变 |
如果该公司今年(2002年)有5名职工,计划从明年起每年新招5名职工。(1)若今年算第一年,试把第n年该公司付给职工工资总额y(万元)表示成年限的函数;(2)试判断公司每年发给职工工资总额中,房屋补贴和医疗费的总和能否超过基础工资总额为20%。
21.已知椭圆C的中心在坐标原点O,焦点在x轴上,离心率为![]() ,过点(1,0)的直线交椭圆于P,Q设PQ的中点为M,且OM的斜率为
,过点(1,0)的直线交椭圆于P,Q设PQ的中点为M,且OM的斜率为![]() ,若椭圆C上存在一点与右焦点关于直线PQ对称,求直线PQ和椭圆C的方程。
,若椭圆C上存在一点与右焦点关于直线PQ对称,求直线PQ和椭圆C的方程。
22.已知二次函数![]() ,设方程f(x)=x的两上实根为
,设方程f(x)=x的两上实根为![]() (1)如果
(1)如果![]() ,设函数f(x)的图象的对称轴为
,设函数f(x)的图象的对称轴为![]() ,求证:
,求证:![]() ;(2)如果
;(2)如果![]() ,求b的范围。
,求b的范围。
参考答案
一.
1、D 2、A 3、C 4、B 5、C 6、D 7、A 8、B 9、A 10、C 11、B 12、D
二.
13.![]()
14.![]()
15.-1
16.22
三.
17.解:
∵![]() ∴
∴![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
(1)∴tgC=-tg(A+B)=-1
∵O<C<π∴![]()
(2)∵![]() tgA>tgB
tgA>tgB
∴C>A>B ∴b为最短边
由正弦定理 ![]()
18.解
(1)∵△POC为等边三角形,E为DC中点
∴PE⊥DC
∵平面PDC⊥平面ABCD
∴PE⊥平面ABCD
∴PE⊥AB
∵ABCD为菱形∠BND=60°E为DC中点
∴BE⊥DC,DC∥AB ∴AB⊥BE
∴AB⊥平面PBE
(2)∠APB为DA与平面PBE所成的角
∵ABCD是边长为a的菱形∠BAD=60°且△PDC为等边三角形
∴AB=a ![]()
∴![]()
∴![]()
∴![]()
(3)∵PE⊥平面ABCD作EH⊥AD于H连PH
∴PH⊥AD∠PHE为二两角P—AD—B的平面角
![]()
∴![]()
∴![]()
19.解:
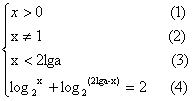
由(4)∴![]()
![]()
∴0.01<a<100时,![]() 方程无实根
方程无实根
又∵2lga>x>0 ∴a>1
∴0<a<100 时原方程无解
当a=100时,方程为![]() ,
,
∴x=2且满足(1)(2)(3)
∵x≠1且当x=1时 ![]() ,即
,即![]()
∴![]() 时,方程为
时,方程为![]()
∴x=4或x=1(舍)
当a>100且![]() 时
时![]() 满足(1)(2)(3)
满足(1)(2)(3)
综上所述:
当0<a<100时方程无解
a=100时,方程有唯一解
![]() 时方程有唯一解x=4
时方程有唯一解x=4
a>100且![]() 时,方程有两解
时,方程有两解![]()
20.解:
(1)第n年共有5n个职员,基础工资总数为:![]() 万元
万元
房屋补贴5×400n+5×400(n-1)……+5×400
=0.1n(n+1)(万元)
医疗费:5n×0.16=0.8n(万元)
∴![]()
(2)基础工资的20%为![]() (万元)
(万元)
房屋补贴和医疗费总和为![]()
要比较![]() 与
与![]() 的大小
的大小
只须比较![]() 与0.1n+0.9n的大小
与0.1n+0.9n的大小
∵![]()
∴房屋补贴和医疗费的总和不能超过基础工资总额的20%。
21.解:
设椭圆C的方程为![]()
∵离心率![]()
∴![]()
∴椭圆方程为![]()
设直线PQ方程:y=k(x-1)
∴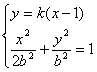
∴![]()
∴![]()
∴![]()
∴![]() ,
,
∴![]()
k=-1
∴直线PQ方程y=-(x-1)即x+y-1=0
设与右焦点下(b,0)关于直线x+y-1=0对称的点为![]()
∴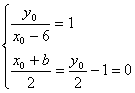
∴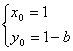
又![]() 在椭圆上
在椭圆上
∴![]()
∴![]()
∴椭圆方程为![]()
22.解:
∴![]()
∴![]()
令 ![]()
∵g(x)=0的两根![]() ,
,![]() 满足
满足![]() 且a>0
且a>0
∴![]()
∴![]()
∴4a-2b>0
∴![]()
∴![]()
(2)∵![]()
∴![]() ,
,![]()
∵![]() ,
,![]()
若![]() ,则
,则![]()
![]()
∴![]()
∴g(2)=4a+2b-1<0
又![]()
∴![]()
∴![]()
∴![]()
∴![]()
![]() 则
则![]() ,
,
![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 时
时![]()
![]() 时
时![]()