综合练习（六）
2002.6 班级：_________，姓名：______________，成绩：___________
一．选择题：（每小题5分，共5×12=60分）将正确答案填入下表中
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
1．设
，
，若
，则a的取值范围是（ ）
A．
B．
C．
D．
2．（理）设函数
，
与
的图像分别记为
、
与
，则 （ ）
A．、、都相同
B．只有与相同
C．只有与相同
D．、、都不相同
（文）把函数
的图象向左平移
个单位，再将图像上所有点的横坐标伸长到原来的2倍（纵坐标不变）所得的图象解析式为
，则（ ）
A．
B．
C．
D．
3．已知
，函数y=sinx在区间D内可能既有最大值又有最小值，则区间D可以是（ ）
A．
B．
C．
D．
4．设O是矩形ABCD的边CD上一点，以直线CD为轴旋转这个矩形所得的圆柱体的体积为V，其中以OA为母线的圆锥的体积为
，则以OB为母线的圆锥的体积等于（ ）
A．
B．
C．
D．
5．将曲线C向右平移3个单位，再向下平移1个单位得到曲线
，若曲线的方程为
，则曲线C的焦点坐标为（ ）
A．
B．
C．
D．（3，2），
6．三个互不相等的实数a、1、b依次成等差数列，且
、1、
依次成等比数列，则
的值是（ ）
A．2
B．
C．2或
D．不确定
7．函数
，则不等式
的解集是（ ）
A．
B．
C．（0，1）
D．
8．登山运动员共10人，要平均分为两组，其中熟悉道路的4人，每组都需分配到2人，那么不同的分组方法的种数是（ ）
A．240
B．120
C．60
D．30
9．（理）直线
和圆
的位置关系是 （ ）
A．相离
B．相切
C．相交
D．相离或相交
（文）过抛物线
的焦点的弦AB两端点的横坐标分别是
，
，若+=6，则AB的长是（ ）
A．10
B．8
C．7
D．6
10．如图，三棱台
中，已知
，
，高为h，则四面体
的体积为（ ）
A．
B．
C．
D．
11．（理）已知
和
是方程
的两根，则动点 (p，q)的轨迹图形是（ ）
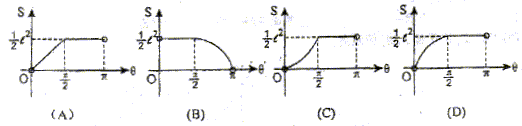
（文）若圆锥的母线长是定值
，过圆锥顶点的截面为等腰三角形，设其顶角为
，过顶点的最大截面的面积为S，则S=
的图象是（ ）
12．已知双曲线
=1和椭圆
的离心率互为倒数，那么以a，b，m为边长的三角形是（ ）
A．锐角三角形
B．直角三角形
C．钝角三角形
D．锐角或钝角三角形
二、填空题：（每小题4分，共
分）
13．在长方体
中，若
，则
与
所成的角是__________。
14．当x=3时，不等式
（a为常数，a>0且
）成立，则不等式的解集是_____________________。
15．一串节日装饰彩灯，由20个灯泡串联而成，只要有一个灯泡坏了，整串灯泡就不亮，则因灯泡损坏而使整串灯泡不亮的可能性总数为______________。
16．定义运算
，则对复数
，x>0），符合条件
的点在复平面上所表示的曲线形状是____________。
三．解答题：（第17~21题每题12分，第22题14分，共74分）
17．（本小题满分12分）
设A是三角形的一个内角，且
，求
的值。
18．（本小题满分12分）
设数列
是等差数列，
，
，数列
是等比数列，
，若
，
，且
。
（1）求数列，的通项公式；
（2）当自然数n取何值时，
？
19．（本小题满分12分）
如图：在棱长为a的正方体
中，E，F分别为棱AB和BC的中点，EF交BD于H。
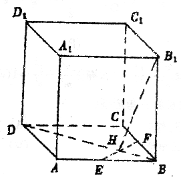
（1）求二面角
的正切值；
（2）试在棱
上找一点M，使
⊥平面
，并证明你的结论；
（3）求点
到平面的距离。
20．（本小题满分12分）
某渔业公司今年初用98万元购进一艘渔船，用于捕捞，第一年需各种费用12万元，从第二年开始包括维修费在内，每年所需费用均比上一年增加4万元，该船每年捕捞的总收入为50万元。
（1）该船捕捞几年开始盈利（即总收入减去成本及所有费用之差为正值）？
（2）该船捕捞若干年后，处理方案有两种。
①当年平均盈利达到最大值时，以26万元的价格卖出；
②当盈利总额达到最大值时，以8万元的价格卖出。
问哪一种方案较为合算？请说明理由。
21．（本小题满分12分）
已知椭圆的中心在坐标原点，焦点在x轴上，它的一个焦点为F，M是椭圆上的任意点，MF的最大值和最小值的几何平均数为2。椭圆上存在着以y=x为轴的对称点
和
，且
，试求椭圆的方程。
22．（本小题满分14分）
设函数
（a、b为实数），
（1）若
，且对任意实数均有
成立，求F(x)的表达式；
（2）在（I）的条件下，当
时，
是单调函数，求实数k的取值范围；
（3）若f(x)是偶函数，试判断F(x)的奇偶性。
参考答案
一、选择题：每小题5分共60分
1．A 2．（理）D （文）B 3．D 4．C 5．B 6．B 7．B 8．C
9．（理）A （文）B 10．A 11．（理）C （文）D 12．B
二．填空题：每小题5分共60分
13．
14．
15．
16．抛物线
三．解答题：
17．∵
∴
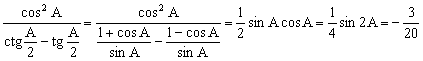
∵A为三角形内角，∴
即：
∴
，
而
∴
18．（1）设
，
。
由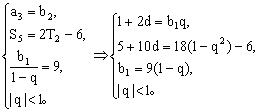
由前三式可得：
，解得：
或
。
而
，∴。
∴代入条件得，
，
。∴
，
。
（2）
，
令，∴
即
。
∵
当
时为增函数，而
。
要使，只要使
由时，
，检验n=4，5，…，可知n>4时，总成立。
19．（1）连AC，
，则
∵
，∴
。
∵
平面ABCD，∴
∴
为二面角的平面角，
在
中，
，
，∴
。
（2）在棱上取中点M，连，∵
平面
，∴
。在正方形
中，∵M，F分别为，BC的中点∴
。
又∵
。
∴
，∴
（3）设与平面交于点N，则
为点到平面的距离
在
中，
∵
，
，
故点到平面的距离为
a
20．解：（1）设捕捞n年后开始盈利，盈利为y元，则：
由y>0，得
∴
∴
∴n=3
即捕捞3年后，开始盈利。
（2）①平均盈利为
当且仅当
即n=7时，年平均利润最大
∴经过7年捕捞后年平均利润最大，共盈利为
万元
②∵
∴当n=10时，y的最大值为102，
即经过10年捕捞盈利额最大，共盈利102+8=110万元，
故两种方案获利相等，但方案②的时间长，所以方案①合算。
21．解：
，
，则
∴
设椭圆方程为：
①
设过和的直线方程为：
②
将②代入①得：
③
设
，
，
的中点为
则
代入y=x得
，由于
，∴m=0
∴由③知：
，
又
∴
，解得：
，
所求椭圆方程为：
。
22．（1）∵∴b=a+1。
由恒成立，知
，
∴a=1，从而
。
∴
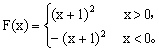
（2）由（1）知，
，∴
由
在
上是单调函数，知：
或
∴得
或
。
（3）∵f(x)为偶数，∴
，而a>0
∴f(x)在
是增函数。
对于F(x)，当x>0时，
，
，
当x<0时，
，
。
∴F(x)是奇函数，且F(x)在上是增函数。