解析几何综合练习
2002.4
班级:_______;姓名:__________;成绩:_______
一.选择题:(每小题4分,共4×10=40分)将正确答案填入下表中
1.![]() 是直线:
是直线:![]() 上一点,
上一点,![]() 是l外一点,则方程
是l外一点,则方程![]() 表示的直线
表示的直线
(A)与l重合
(B)与l相交于P点
(C)过Q点且与l平行
(D)过Q点且与l相交
2.已知椭圆![]() 的离心率
的离心率![]() ,则m的值为
,则m的值为
(A)3 (B)![]()
(C)3或![]() (D)
(D)![]() 或
或![]()
3.设双曲线![]() 的一条准线与两条渐近线交于A,B两点,相应的焦点为F,若△ABF是正三角形,则双曲线的离心率为
的一条准线与两条渐近线交于A,B两点,相应的焦点为F,若△ABF是正三角形,则双曲线的离心率为
(A)![]() (B)3
(B)3
(C)![]() (D)2
(D)2
4.(理)参数方程![]()
![]() ,它所表示的曲线是
,它所表示的曲线是
(A)圆周(B)椭圆
(C)二分之一椭圆(D)四分之一椭圆
(文)与直线2x+3y-6=0关于点(1,-1)对称的直线是
(A)3x-2y+2=0
(B)3x+4y+7=0
(C)3x-2y-12=0
(D)2x+3y+8=0
5.把直线![]() 绕原点逆时针方向旋转,使它与圆
绕原点逆时针方向旋转,使它与圆![]() 相切,则直线旋转的最小正角是
相切,则直线旋转的最小正角是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
6.平移坐标系,使原点移至(-2,0),这时双曲线![]() 化为标准方程,则此双曲线在原坐标系中的渐近线方程是
化为标准方程,则此双曲线在原坐标系中的渐近线方程是
(A)![]()
(B)![]()
(C)![]()
(D)![]()
7.若直线:![]() 与圆
与圆![]() 的两个交点关于直线
的两个交点关于直线![]() 对称,那么这两个交点的坐标是
对称,那么这两个交点的坐标是
(A)(3,-2)(-2,-3)
(B)(3,-2),(2,-3)
(C)(1,2),(-2,-1)
(D)(-1,2),(1,-2)
8.AB是抛物线![]() 的一条弦。若AB的中点到x轴的距离为1,则弦AB长度的最大值为
的一条弦。若AB的中点到x轴的距离为1,则弦AB长度的最大值为
(A)![]() (B)
(B)![]()
(C)2(D)4
9.对于抛物线![]() 上任意一点Q,点P(a,0)都满足PQ≥a,则a的取值范围是
上任意一点Q,点P(a,0)都满足PQ≥a,则a的取值范围是
(A)(-∞,0)(B)(-∞,2]
(C)[0,2](D)(0,2)
10.△ABC的顶点A(3,-1),AB边上的中线所在直线的方程为x+y-8=0,直线![]() 是过点B的一条直线,则AB的中点D到直线l的距离是
是过点B的一条直线,则AB的中点D到直线l的距离是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
二.填空题:(每小题4分,共4×5=20分)
11.已知定点F(4,0)和定直线l: x=-4,动点P在直线l上,直线![]() 过点P且与直线l垂直,直线
过点P且与直线l垂直,直线![]() 垂直平分线段PF,又直线
垂直平分线段PF,又直线![]() 与
与![]() 交于M,则点M的轨迹方程是________。
交于M,则点M的轨迹方程是________。
12.(理)在极坐标系中,已知一个圆的方程是![]() ,则通过圆心与极轴垂直的直线的直角坐标方程是________
,则通过圆心与极轴垂直的直线的直角坐标方程是________
(文)若双曲线![]() 的一条准线恰为圆
的一条准线恰为圆![]() 的一条切线,则k=______
的一条切线,则k=______
13.椭圆![]() 与连结A(1,2),B(2,3)的线段没有公共点,则正数a的取值范围是_________
与连结A(1,2),B(2,3)的线段没有公共点,则正数a的取值范围是_________
14.P为抛物线![]() 上一点,它到抛物线准线的距离记为
上一点,它到抛物线准线的距离记为![]() ,到直线x+2y-12=0的距离为
,到直线x+2y-12=0的距离为![]() ,则
,则![]() 的最小值为______
的最小值为______
15.命题:①方程![]() 表示的曲线是圆;②椭圆
表示的曲线是圆;②椭圆![]() 的两条准线方程是x=-2和
的两条准线方程是x=-2和![]() ;③抛物线
;③抛物线![]() 的焦点坐标为
的焦点坐标为![]() ④双曲线
④双曲线![]() 的渐近线方程为
的渐近线方程为![]() 。其中正确命题的序号是______
。其中正确命题的序号是______
三.解答题:(每题10分,共40分)
16.直线y=3x与抛物线![]() 交于A,B两点,点P在抛物线被直线AB截得的一段弧上,(1)求△PAB面积最大时,P点的坐标(
交于A,B两点,点P在抛物线被直线AB截得的一段弧上,(1)求△PAB面积最大时,P点的坐标(![]() );(2)与AB平行的直线和抛物线交于C,D两点,证明线段CD被直线
);(2)与AB平行的直线和抛物线交于C,D两点,证明线段CD被直线![]() 平分。
平分。
17.一辆卡车高3米,宽1.6米,欲通过断面为抛物线型的隧道,已知拱口宽恰好是拱高的4倍,若拱口宽为a米,求能使卡车通过的a的最小整数值。
18.设双曲线满足:(1)渐近线方程为x+2y=0及x-2y=0;(2)点A(5,0)到双曲线上动点P的距离的最小值为![]() 。同时满足(1),(2)的双曲线是否存在?若存在,求其方程;若不存在,说明理由。
。同时满足(1),(2)的双曲线是否存在?若存在,求其方程;若不存在,说明理由。
19.已知椭圆![]() 的一条准线的方程为x=1.又倾斜角为45°的直线交该椭圆于A,B两点,A,B的中点为M,直线AB与OM的夹角为α(1)当tgα=2时,确定此时椭圆的方程;(2)当2<tgα<3时,求b的取值范围。
的一条准线的方程为x=1.又倾斜角为45°的直线交该椭圆于A,B两点,A,B的中点为M,直线AB与OM的夹角为α(1)当tgα=2时,确定此时椭圆的方程;(2)当2<tgα<3时,求b的取值范围。
参考答案
一.
1 C 2 C 3 D 4 D 5 B 6 A 7 C 8 B 9 B 10 A
二.
11.![]()
12.x=3 48
13.![]()
14.![]()
15.③
三.
16(1)
∴![]()
∴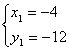

∴![]()
∵![]() 在抛物线弧上,
在抛物线弧上,
∴![]()
∴P到AB的距离![]()
∴![]()
∴当![]() 时
时![]()
∴![]()
(2)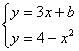
∴![]()
△x=9-4(b-4)>0
∴![]()
又![]()
∴![]()
∴CD中点必在直线![]() 上,即CD被
上,即CD被![]() 平分
平分
17.解:
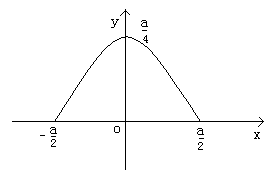
如图建立直角坐标系,则抛物线方程为
![]()
∵抛物线过点![]()
∴![]()
∴2p=a
∴抛物线方程为![]()
要使卡车通过,则![]()
∴![]()
∵a>0
∴![]()
∴a的最小正整数值为13.
18.解:
设双曲线方程为![]()
其中一点![]()
∴![]()
若m>0 则![]()
∴![]()
当![]() 即
即![]() 时.
时. ![]()
∴![]()
∴m=-4与m>0矛盾
∴当![]() 即m>16时,
即m>16时,
![]()
∴![]()
∴![]() 或
或![]() (舍)
(舍)
∴![]()
若m<0则x∈R
∴![]()
![]()
∴m=-4
∴同时满足条件①②的双曲线存在,其方程为
![]() 或
或![]()
19.解:
设![]()
∵![]() ∴
∴![]()
![]()
∴椭圆方程为![]()
即![]()
设直线NB方程为y=x+m
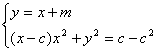
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
(1)∵![]()
∴![]() 或c= -2(舍)
或c= -2(舍)
∴椭圆方程为![]()
(2)![]() ∴
∴![]()
∴
∴![]()
∴![]()
![]()
∴![]()
∴![]()