单元练习十五圆锥曲线（二）
2002.4
班级：_______；姓名：_______；成绩：______
一．选择题：（每小题5分，共5×10=50分）将答案填入下表中
1．已知
、
是抛物线
上不同的两点，则
是直线
通过抛物线焦点的
（A）充分不必要条件
（B）必要不充分条件
（C）充要条件
（D）既不充分也不必要条件
2．P是抛物线
上的动点，点A（0,-1），点M在直线PA上且分PA所成的比为2：1，则点M的轨迹方程是
（A）
（B）
（C）
（D）
3．P为椭圆
上的动点，过点P作椭圆长轴的垂线，垂足为M，则PM中点的轨迹方程是
（A）
（B）
（C）
（D）
4．过定点A（0，a）且在x 轴上截得弦长为2a的动圆圆心的轨迹方程是
（A）
（B）
（C）
（D）
5．设P(x,y)是椭圆
上的动点，则
的最小值是
（A）
（B）
（C）
（D）
6．抛物线
上点到直线2x-y-4=0的距离最短的点的坐标是
（A）
（B）（1,1）
（C）
（D）（2,4）
7．过双曲线
的右焦点作直线l交双曲线于A,B两点，若AB=4，则这样的直线存在
（A）1条（B）2条
（C）3条（D）4条
8．过点M（-2，0）的直线l与B椭圆
交于
,
两点，线段
的中点为P，设直线l的斜率为
，直线OP的斜率为
，则
的值等于
（A）2（B）-2
（C）
（D）
9．已知直线l交椭圆
于M，N两点，椭圆与y轴的正半轴交于B点，若△BMN的重心恰是椭圆的右焦点，则直线l的方程为
（A）5x+6y-28=0（B）5x-6y-28=0
（C）6x+5y-28=0（D）6x-5y-28=0
10．设双曲线
的左准线与x轴的交点是M ，则过M与双曲线恰有一个交点的直线共有
（A）2条（B）3条
（C）4条（D）无数条
二．填空题：（每小题5分，共5×10=50分）
11．设O为坐标原点，直线
与抛物线
交于P，Q两点，则∠POQ等于_____
12．直线x-y-1=0与实轴在y轴上的双曲线
的交点在以原点为中心，边长为2且各边分别平行于坐标轴的正方形的内部，则m的取值范围是___________
13．设连结双曲线
与
的四个顶点的四边形的面积为
，连结四个焦点的四边形的面积为
，则
的最大值是______
14．方程
所表示的曲线为C，①：若曲线C的离心率e∈(0,1)，则1<t<4；②若曲线C为双曲线，则t<1或t>4；③：曲线C不可能是圆；④：若曲线C表示长轴在x轴上的椭圆，则1<t<2.5。上述命题中正确的序号是_______
15．直线2x-2y+3=0被抛物线
截得的线段长是_________
16．若无论b取任何实数，直线y=kx+b与双曲线
总有公共点，那么k的取值范围是______
17．中心O（0,0），一焦点为
，截直线y=3x-2所得弦的中点的横坐标为的椭圆的方程为________
18．△ABC的三个顶点都在以原点为焦点x轴为对称轴的抛物线上。若A点的坐标为（-6，8），且△ABC的重心在原点，则直线BC的方程是_______
19．双曲线的离心率e=2，虚轴长为6，
，
分别是它的左、右焦点，若过的直线与双曲线的左支交于A，B两点，且
，AB，
成等差数列，则AB=_______
20．直线y=1-x交椭圆
于M，N两点，弦MN的中点为P。若
，则
三．解答题：（共50分）
21．已知A，B是两个定点，且AB=2，动点M到点A的距离是4，线段MB的垂直平分线l交MA于点P.（1）当M点运动时，建立适当的坐标系，求动点P轨迹C的方程，并说明轨迹C是什么图形；（2）设点Q是以A，B为焦点，实轴长为1的双曲线与（1）中轨迹C的交点，求tg∠AQB的值.
22．已知抛物线
，直线x-2y=0.（1）求证：抛物线与直线总有两个交点；（2）设抛物线的顶点为M，证明：无论m为何实数，点M不在直线x-2y=0上；（3）设直线与抛物线两个交点为A，B，当∈[2，5]时，求△AMB面积的最大值和最小值。
23．直线y=kx+1与双曲线
的左支相交于A，B两点，直线l过点（-2，0）和AB的中点，求直线l和y轴上的截距b的取值范围。
24．已知点
在椭圆
上，过A作两条直线与椭圆交于B、C两点，若直线AB、AC与x轴围成以∠A为顶角的等腰三角形.（1）求直线BC的斜率；（2）求使△ABC的面积最大时直线BC的方程。
参考答案
一．
1 C 2 A 3 B 4 D 5 C 6 B 7 C 8 D 9 D 10 C
二．
11．90°
12．（-1,0）
13．
14．②④
15．
16．
17．
18．4x+y-8=0
19．
20．
三．
21．解：
（1）如图直线AB为x轴，AB中点O为原点建立直角坐标系
则M（-1,0）B（1，0）设P（x,y）
∵PB=PM MA=4
∴PM+PB=4
∴P点轨迹是以A，B为焦点且长轴长为4的椭圆.
其方程为
（2）不失一般性. 设Q点在第一象限
∴
∴
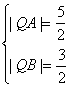
由余弦定理
∴
22．解：
（1）
∴
∵
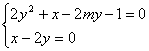
∴直线与抛物线长总有两个公共点.
（2）∵
∴
∵
∴M点不在直线x-2y=0上
（3）∵
，
∴
点M到直线x-2y=0的距离
∴
∵m∈[2,5]时
递增且恒正
递增且恒正
∴
在[2，5]上为增函数
∴m=2时
，m=5时
23．解：
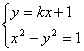消y
∴
∵直线与双曲线的右支交于A，B两点
∴
∴
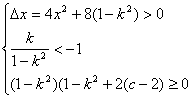
又AB中点
∴l方程
∴
∴
或b>2
24．解：
∵在椭圆上
∴n=4椭圆方程：
（1）设直线AB的斜率为k，则AC斜率为-k
∴直线AB方程：
∴
∴
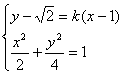
同理可得
∴
（2）设直线BC方程为
∴
∴
∴
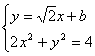
又
，
∴
又点A到直线BC的距离
∴
当且仅当
，而b=±2时，等高成立.
∴
，此时BC方程为