代数综合练习（一）
2002．4
班级：___________;姓名：______________; 成绩：_____________
一．选择题：（每小题4分，共4×10=40分）将正确答案填入下表中
1．设集合A={x1<x≤2},B={xx-a>0}，当A∩B=A时，实数a的取值范围是
（A）[2，+∞）（B）（-∞，1]
（C）（-∞，1）（D）（2，+∞）
2．下列函数：①
；②
；③
；④
其中值域是（0，+∞）的函数有
（A）1个（B）2个
（C）3个（D）4个
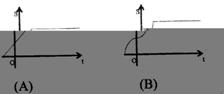
3．如图，四边形OABC是正方形，在直线l:y=x+t下方的面积为S，当直线l由下而上匀速移动时，面积S关于t的函数图象是
4．定义在R上的偶函数f(x)，满足f(3+x)=f(3-x),且在[-3，0]上单调递减，
设a=f(-1.5),b=f(7),c=f(4),则a,b,c的大小顺序为
（A）b<c<a（B）a<b<c
（C）b<a<c（D）c<b<a
5．奇函数f(x)的定义域是R，函数
。若g(1)=4，则g(-1)的值等于
（A）-1；（B）-2；
（C）-3；（D）无法确定；
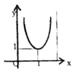
6．已知函数y=f(x)的图象如右图，则函数
的图象是
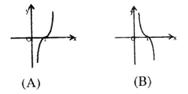
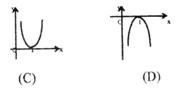
7．不等式
的解集是
（A）（0，1）；
（B）
（C）
；
（D）
；
8．若
，则(1+ab)(1-ab)的最大、最小值分别是
(A)1和
；(B)1和0；
(C) 和0；(D) 和
；
9．已知函数f(x)=-2x+1对任意正数ε，使得
成立的一个充分但不必要条件是
（A）
；
（B）
；
（C）
；
（D）
；
10．原市话资费为每3分钟0.18元，现调整为前3分钟资费为0.22，超过3分钟，每分钟0.11元，与调整前相比较，一次通话提价的百分比
（A）不会高于70%
（B）会高于70%而不会高于90%
（C）不会低于10%
（D）高于30%而低于100%
二．填空题：（每小题4分，共4×5=20分）
11．方程
的解集是___________________
12．函数
的反函数是_______
13．将桶1的水到入桶2，开始时桶1中有水a升，t分钟后剩余的水符合指数衰减曲线
，那么桶2中的水就是
。假设过5分钟两桶的水相等，则再过___________分钟桶1中的水只有
。
14．设（-∞，a） 是函数
的反函数的一个单调递增区间，则实数a的取值范围是____.
15．设函数f(x)=xx+bx+c，给出四个命题：①c=0时，f(x)是奇函数；②b=0,c>0时，方程f(x)=0只有一个实根；③f(x)的图象关于点（0，c）对称；④方程f(x)=0至多有两个实根，其中正确命题的序号是____________
三．解答题：（每题10分，共40分）
16．解关于x的不等式：
（a>0且a≠1）
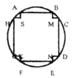
17．有一种变压器的铁芯的截面是正十字形，即矩形ABEF与矩形CDGH全等，且AS=KF=HS=MC。为保证所需的磁通量，要求正十字形面积为
。为了使绕铁芯所用的铜线最省，即正十字形的外接圆周长最小，应如何设计正十字形的长和宽（即确定AB与BE的长度？）
18．设f(x)是定义在[-1，1]的奇函数，g(x)的图象与f(x)的图象关于直线x=1对称，而当x∈[2,3]时，
（c为常数）。
（1）求f(x)的表达式；
（2）对于任意
，
且
，求证：
；
（3）对于任意，且，求证：
19．已知f(x)是定义在[-1，1]上的奇函数，且f(1=1)。若a,b∈[-1，1],a+b≠0有
（1）判断函数f(x)在[-1，1]上是增函数还是减函数，证明你的结论；
（2）解不等式
；
（3）若
对一切x∈[-1,1],a∈[-1,1]恒成立，求实数m的取值范围。
参考答案
一．
1、B 2、A 3、C 4、C 5、B 6、D 7、D 8、A 9、C 10、B
二．
11．{0}
12．
13．10
14．a≤-2
15．①②③
三．
16．解：∵
∴x>0
若0<a<1则
∴
∴
∴
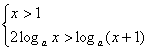
若a>1则
∴0<x<1或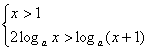
∴0<x<1或
综上所述，当0<a<1时不等式的解集为
当a>1时不等式的解集为
17．解：连结AE设AB=x，BE=y外接圆直径AE=d，周长为C
∴
∴
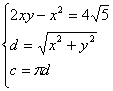
当且仅当
即x=2时等式成立，此时
∴AB=2cm
cm时，其外接圆周长度小。
18．解：
∵g(x)的图象与f(x)的图象关于直线x=1对称
∴f(x)=g(2-x),又2-x∈[2.3]时x∈[-1,0]
∴
又f(x)是奇函数∴f(0)=4+c=0∴c= - 4
∴
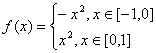
(2)∵
∴
∴
(3)∵
∴
，
∴
∴
∴
19．解：
（1）
∴
∵
是奇函数
∴
∴
∴f(x)在[-1，1]上递增
（2）
∴
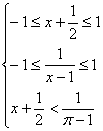
（3）∵f(x)在[-1，1]上递增且f(1)=1
∴要使对任意x∈[-1,-1], 任意a∈[-1,1]成立
则对任意a∈[-1,1] 
恒成立. 即
恒成立
令
∴g(c)是关于a的单调函数
∴
∴
∴m≤-2或m≥2或m=0