高三数学上学期直线和平面练习

第七章　　　  直线和平面

 (一)选择题

1.有下列四个命题：

(1)n条直线中，若任意两条都共面，则这n条直线都共面

(2)分别与两条异面直线都相交的两条直线是异面直线

(3)空间中有三个角是直角的四边形是矩形

(4)两条异面直线在同一平面内的射影不可能是平行线

其中，真命题的个数为(　　)

A.0　　　  B.1　　　  C.2　　　　D.3

2.下列命题中，真命题是(　　)

A.若直线m、n都平行于平面α则m∥n

B.设α—l—β是直二面角，若直线m⊥l,则m⊥β

C.若m、n在平面α内的射影依次是一个点和一条直线，且m⊥n,则n在α内或n与α平行

D.若直线m、n是异面直线，若m与平面α平行，则n与α平行，则n与α相交

3.已知直线a、b和平面α，下列命题正确的是(　　)

(1)　　　　　　  (2)

(3) 　　　　　　 (4)  

A.(1)(2)　　　　　　 　　　　　　B.(1)(2)(3)

C.(1)(2)(4)　　　　　　　　　　  D.(2)(3)(4)

4.设α、β是两个不重合的平面，m和l是两条不重合的直线，则α∥β的一个充分条(　　)

A.lα，mα且l∥β，m∥β

B.lα， mβ且l∥m

C.l⊥α，m⊥β，且l∥m

D.l∥α，m∥β且l∥m

5.四棱柱成平行六面体的充分但不必要条件是(　　)

A.底面是矩形　　　　　　　　　　　B.侧面是平行四边形

C.一个侧面是矩形　　　　　　　　  D.两个相邻侧面是矩形

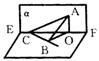
6.二面角α—EF—β是直二面角，C∈EF，ACα，BCβ，如果∠ACF=30°，∠ACB=60° ，∠BCF=θ，那么cosθ的值等于，则(　　)

A.　　  B.　　　 C.　　 D.

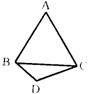
7.如图，有共同底边的等边△ABC和等边三角形BCD所在平面互相 垂直，则异面直线AB和CD所成角的余弦值为(　)

A.　　　　B.　　  C.　 　　 D.

8.正方体ABCD—A₁B₁C₁D₁中截面AB₁C和截面A₁B₁C所成的二面角的大小(　　)

A.45°　　　　　　　　　　　　　B.60°

C.arccos　 　　　　　　　　 D.arccos

9.如图，BCDE是一个正方形，AB⊥平面CE，侧图中相互垂直的平面有(　　)

A.3组　　　　　　 B.6组

C.7组　　　　　　 D.8组

10.正方形ABCD-A₁B₁C₁D₁中，平面A₁BC₁与平面ABCD所成二面角的正弦值是(　　)

A.　　  B.　　   C.　　   D.

(二)填空题

11.两条异面直线所成的角为θ，则cosθ的取值范围是　　　　　　　 .

12.棱长为1的正方体，PA、PB、PC是共一个顶点P的三条棱，那么点P到平面ABC的距离是　　　　　　　 .

13.从三棱锥六条棱的中点中，任选四个作为四边形的顶点.其中为平行四边形的个数有 个.

14.正方体ABCD所在平面与正方形ABEF所在平面成60°的二面角，则异面直线AD与BF所成角为　　　　.

15.正四棱锥S-ABCD的高为2，底面边长为，P、Q两点分别在线段BD和SC上 ，则P、Q两点的最短距离为　　　　  .

(三)解答题

16.已知平面α和不在这个平面内的直线a都垂直于平面β，求证a∥α.

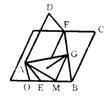
17.如图，正方形ABCD，E、F分别在AB、CD的中点，G为BF的中点，现将正方形沿EF折成 120°的二面角.求①异面直线EF和AG所成的角；②AG和平 面EBCF所形成的角.

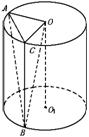
18.圆柱底面半径是3，高是4，A与B分别是两底的圆周上的点，且AB＝5，求异面直线AB与OO ₁间的距离。

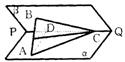
19.如图，已知二面角α-PQ-β为60°，点A和B分别在平面α和平面β内，点C在棱PQ 上，且∠ACP=∠BCP=30°AC=BC　①求证AB⊥PQ；②求直线PQ

在面ABC所成角的大小.

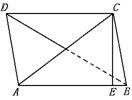
20.如图，设ABCD是矩形，沿对角线DB将ABDC折起，使点C在底面DAB上的射影E恰好落在 AB边上

(1)求证：平面ABC⊥平面ACD。

(2)若AB＝2，BC＝，求二面角C-AD-B的大小及三棱锥C-ABD的体积。

 参考答案：

 (一)　1.B　2.B  3.A　4.C　5.A  6.D　7.B　8.D  9.C　10.A

提示：

6.作AO⊥EF，垂足是O，作OB⊥BC，垂足是B，连AB，易知AO⊥β，AB⊥BC，设AC=a，可得 C O=a，CB=，cosθ=.

7.作AO⊥BC，连OD，作BE∥DC，DE∥BC交BE于E，连AE.易知∠ABE(或补角)即异面直线AB、C D据所成的角，且AB⊥DE，设正三角形边长为a，可得AB=a，BE=a，AE=a，由余弦定理得cos∠ABE=-，异面直线所成角的余弦值是.

8.设二面角为θ，易知tgθ= (a是正方体棱长).

9.找平面的垂线，即可找出相互垂直的平面，七组是平面ABC和平面ABE，平面ABC和平面BD ；平面ABE和平面BD；平面ABD和平面BD；平面ABD和平面ACE；平面ABC和平面ACD；平面ADF 和平面ABE.

  (二)  11.［0，1］　12.　13.3　14.arccos　15.

(三)  16.设α∩β=DE，在平面α内作CB⊥DE，则CB⊥β.

∵α⊥β，∴a∥CB，又∵aα，∴a∥α，

17.①作GM∥EF，则∠AGM是异面直线EF和AG所成的角，可知∠AEM是二面角A-EF-B的平面角 ，∠AEM=120°，又可证　AM⊥MG，设正方形边长为4a，得GM=2a，AM=a，

∴tg∠AGM=，异面直线AG和EF成角为arctg.

②作AO⊥平面BF，O在BE延长线上，连GO，则∠AGO是AG与平面BF所成的角；AO=a，OG=2a，tg∠AGO=，AG与平面EBCF所成角为arctg.

18.解　如图，作母线BC，连结OA、OB、OC、AC，则有：V_O-ABC＝V_B-AOC

OO₁∥BC且BC在ABC，OO₁面ABC

OO₁∥面ABC

设O到平面ABC的距离为d，则所求为d

BC⊥⊙O所在平面，AC⊙O所在平面

BC⊥AC，而BC＝4，AB＝5故AC＝3

△AOC是边长为3的正三角形

(AC·BC)·d＝(·AC²·sin60°)·BC

解之d=

19.①过B 作BD⊥PQ于D连AD，由已知有△BCD≌△ACD，∴AD⊥PQ，∴PQ⊥平面ADB，则PQ⊥AB.

②取AB中点H，连DH、CH，设BC=AC=a，则BD=AD=，CD=a，由①知∠ADB是二面角α-PQ-β的平面角，为60°，且PQ⊥HD， 因此△ABD是正三角形，HD=a.

在Rt△CHD中，tg∠DCH=，∠DCH=arctg，又由∠PCA=∠PCB，知PQ在平面ABC的射影在∠ACB的平分线上，而AC= BC，AH=BH，则CH是∠ACB的平分线，PQ在平面ABC的射影即CH，从而PQ与平面ABC所成的角为 arctg.

20.(1)证明　因CE⊥面ABD

AD面ABD

CE⊥AD

AB⊥AD，CE∩AB=E

AD⊥面ABC，面BC面ABC

AD⊥BC

DC⊥BC、AD∩DC=D

BC⊥面ACD

BC面ABC

面ABC⊥面ACD

(2)解　因AB⊥DA，CE⊥面ABD，AC在平面ABD上的射影为AE由三垂线定理，AC⊥DA

∠CAE是二面角C-AD-B的平面角。

又BC⊥面ACD

BC⊥AC，sin∠CAB=

∠CAB＝60°

C-AD-B是60°的二面角

∠CBE＝30°，CE＝

V_C-ABD＝·CE·(AD·AB)＝××××2＝