高三第一学期期中练习
数学
2002.11
学校________班级________姓名_______
一、选择题:选择题共10个小题,每小题5分,共50分。在每小题给出的四个选项中只有一项是符合题目要求的。
1.设集合A={xx+1>0},集合![]() 则A∪B等于( )
则A∪B等于( )
(A)![]() (B)
(B)![]()
(C)![]() (D){x x>-1}
(D){x x>-1}
2.在数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
(A)![]() (B)10
(B)10
(C)13 (D)19
3.已知复数z满足![]() ,那么复数z的模z等于( )
,那么复数z的模z等于( )
(A)![]() (B)5
(B)5
(C)2
(D)![]()
4.已知函数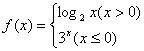 ,那么
,那么![]() 的值为( )
的值为( )
(A)9
(B)![]()
(C)-9
(D)![]()
5.已知函数![]() ,那么它的反函数
,那么它的反函数![]() 的图象大致是( )
的图象大致是( )

6.若a,b∈R,则![]() 成立的一个充分必要条件是( )
成立的一个充分必要条件是( )
(A)a>b>0 (B)b>a
(C)a<b<0 (D)ab(a-b)<0
7.若关于x的不等式![]() ,对任意x∈[0,1]恒成立,则( )
,对任意x∈[0,1]恒成立,则( )
(A)m≤-3 (B)m≥-3
(C)-3≤m≤0 (D)m≥-4
8.2名语文教师2名数学教师分别担任某年级4个班的语文、数学课,每人承担两个班课,不同的任课方法有( )
(A)36种 (B)12种
(C)18种 (D)24种
9.定义域是R的函数f(x)中,对任意两个互不相等的实数a、b总有
![]() 成立,那么一定有( )
成立,那么一定有( )
(A)f(x)在R上是增函数 (B)f(x)在R轴上是减函数
(C)f(x)是奇函数 (D)f(x)是偶函数
10.设 ,对所有实数x均满足xf(x)≤g(x),那么函数g(x)可以是( )
,对所有实数x均满足xf(x)≤g(x),那么函数g(x)可以是( )
(A)g(x)=sinx (B)g(x)=x
(C)![]() (D)g(x)=x
(D)g(x)=x
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
11.若函数![]() ,则不等式
,则不等式![]() 的解集是_______________。
的解集是_______________。
12.当x∈[0,3]时,函数![]() 的最大值是________________。
的最大值是________________。
13.若无穷等比数列![]() 的前n项和为
的前n项和为![]() ,其各项和为S。又
,其各项和为S。又![]() ,则数列
,则数列![]() 的公比为________________。
的公比为________________。
14.有以下四个命题:
①函数![]() 与函数
与函数![]() 的定义域相同;
的定义域相同;
②函数![]() 与
与![]() 的值域相同;
的值域相同;
③函数![]() 与
与![]() 在(0,+∞)上都是增函数;
在(0,+∞)上都是增函数;
④函数![]() 与
与![]() 在其定义域内均是奇函数;
在其定义域内均是奇函数;
其中正确命题的题号为__________________-。
三、解答题:本大题共6个小题,共84分,解答应写出文字说明,证明过程或演算步骤。
15.(本小题满分12分)
解不等式![]()
16.(本题满分12分)
设z是复数,试解方程![]() 。
。
17.(本小题满分14分)
在数列![]() 中,
中,![]() ,
,![]() 其中
其中![]() 表示数列的前n项和。
表示数列的前n项和。
(Ⅰ)分别求![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)求数列![]() 的通项公式
的通项公式![]() 的表达式,并予以证明。
的表达式,并予以证明。
18.(本小题满分16分)
甲、乙两人连续6年对某农村养鸡业的规模进行调查,提供出以下两个不同的信息图及表。甲调查表明:每个养鸡场出产的鸡从第1年1万只上升到第6年2万只。(如表)
| 年 | 1 | 2 | 3 | 4 | 5 | 6 |
| 鸡场养鸡平均只数 | 1.0万 | 1.2万 | 1.4万 | 1.6万 | 1.8万 | 2.0万 |
乙调查表明:(如右图所示)
养鸡场由第一年30个减少到第六年10个。

请你根据这两组信息解答以下问题:
(Ⅰ)求第2年养鸡场的个数及第2年全县出产鸡的总只数;
(Ⅱ)问:到第6年这个县的养鸡总只数比第1年是扩大了还是缩小了?说明理由。
(Ⅲ)求哪一年该县的养鸡总只数规模最大,哪一年规模最小?说明理由。
19.(本小题满分14分)
设二次函数![]() 。若f(x)=0有两个实数根
。若f(x)=0有两个实数根![]() ,
,![]() 。
。
(Ⅰ)求正实数c的取值范围;
(Ⅱ)求![]() 的取值范围;
的取值范围;
(Ⅲ)如果存在一个实数m,使得f(m)<0,证实:![]() 。
。
20.(本小题满分16分)
已知函数![]() 及数列
及数列![]() 。
。
使得2,![]() ,
,![]() ,…,
,…,![]() ,2n+4构成等差数列(n=1,2,…)。
,2n+4构成等差数列(n=1,2,…)。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 的前n项和为
的前n项和为![]() ,当0<a<1时,求
,当0<a<1时,求![]() ;
;
(Ⅲ)若![]() ,当a>1时,试比较
,当a>1时,试比较![]() 与
与![]() 的大小。
的大小。
高三数学第一学期期中练习参考答案及评分标准
一、选择题(每小题5分,共50分)
1C 2C 3A 4B 5A 6D 7A 8A 9A 10D
二、填空题
11.(-1,0)∪(1,+∞)
12.4
13.![]()
14.①,④
三、解答题
15.(本小题满分12分)
解:原不等式可以化成:
![]() 或
或![]() ………………………………………………2分
………………………………………………2分
等价于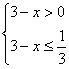 或
或![]() ……………………………………………………8分
……………………………………………………8分
![]() 或
或![]()
所以![]() 或
或![]() …………………………………………………………10分
…………………………………………………………10分
原不等式的解集为(-∞,0]∪[![]() ,3)………………………………………12分
,3)………………………………………12分
16.(本小题满分12分)
解:设z=x=yi,其中x,y∈R……………………………………………………2分
则![]()
原方程可以化成:
(x+yi)(x-yi)-3i(x-yi)=1+3i
![]()
![]() ………………………………………………6分
………………………………………………6分
 ……………………………………………………………………8分
……………………………………………………………………8分
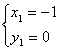 或
或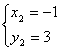 ………………………………………………10分
………………………………………………10分
故![]() ,
,![]() ……………………………………………………12分
……………………………………………………12分
17.(本小题满分14分)
解:(Ⅰ)![]()
![]()
![]() ………………………………3分
………………………………3分
(Ⅱ)由(Ⅰ)猜想数列![]() 的通项公式
的通项公式![]() ……………………5分
……………………5分
以下用数学归纳法证明:①n=1时,![]() ,命题成立;
,命题成立;
②假设n=k(k≥1)时成立,即![]() 成立………………7分
成立………………7分
由已知![]() 推得:
推得:
![]()
成立……………………………………………………………………………………9分
那么,当n=k+1时,

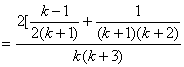
![]()
则n=k+1时,![]() 也成立。……………………………………14分
也成立。……………………………………14分
综上可知,对任意n∈N,![]() 成立。
成立。
18.(本小题满分16分)
解:(Ⅰ)由图象可知:该县第2年养鸡场有26个,由表可知:该年平均每个养鸡场出产1.2万只鸡,所以全县共出产1.2×26=31.2(万只鸡)………………2分
(Ⅱ)依图、表可知:第1年全县产鸡1×30=30(万只)
第6年全县产鸡2×10=20(万只)
因此到第6年全县养鸡总只数比第1年缩小了……………6分
(Ⅲ)依图、表可知:第1年到第6年,每年养鸡场的个数构成首项为30,公差为-4的等差数列,因此第n年养鸡场的个数是:
![]() (n=1,2,…,6)………………………………………………8分
(n=1,2,…,6)………………………………………………8分
又从第1年到第6年,每个养鸡场养鸡平均只数构成首项为1,公差为0.2的等差数列,因此第n年每个养鸡场平均养鸡只数是:
![]() (n=1,2,…,6)…………10分
(n=1,2,…,6)…………10分
因此第n 年全县养鸡的总只数
![]()
![]()
![]() (n=1,2,…,6)………………14分
(n=1,2,…,6)………………14分
可知:当n=2时,即第2年全县养鸡为31.2万只,规模最大。………………15分
显然:![]() ,故第6年全县养鸡规模最小。……………………16分
,故第6年全县养鸡规模最小。……………………16分
(本题也可以根据已知数据逐年算得。)
19.(本小题满分14分)
解:(Ⅰ)由![]() 有两个实数根
有两个实数根![]() ,
,![]() (
(![]() )及c>0得
)及c>0得
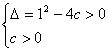 可知:
可知:![]() ……………………………………………2分
……………………………………………2分
(Ⅱ)依根与系数的关系,得: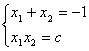 ………………………………4分
………………………………4分
又![]() ,所以,
,所以,![]()
∴![]() ……………………8分
……………………8分
∴故![]() (0,1)
(0,1)
(Ⅲ)证:∵f(m)<0且抛物线![]() 的开口向上
的开口向上
∴![]() ……………………………………………………………………10分
……………………………………………………………………10分
可知:![]()
而![]() ………………………………14分
………………………………14分
20.(本小题满分16分)
解:(Ⅰ)设等差数列的公差为d
则2n+4=2+[(n+2)-1]·d ∴d=2……………………………………………2分
故![]() ……………………………………4分
……………………………………4分
即![]()
∴![]() (a>0且 a≠1)……………………………………6分
(a>0且 a≠1)……………………………………6分
(Ⅱ)∵a≠1
∴![]() ………………………………8分
………………………………8分
∵![]() (当0<a<1时)
(当0<a<1时)
∴![]() ………………………………………………………………10分
………………………………………………………………10分
(Ⅲ)![]()
∴![]() ………………………………13分
………………………………13分
这是因为a>1且![]() 的缘故
的缘故
故![]() ………………………………………………………………………………16分
………………………………………………………………………………16分
(本问利用作差法证明亦可)
囿于篇幅,本答案只写出一种解法,卷面上如有其它解法,请相应给分。